3403

Minimum-TR pulse design for rapid gradient echo sequences

Samy Abo Seada¹, Arian Beqiri¹, Anthony Price¹, Jo Hajnal¹, and Shaihan Malik¹

¹School of Biomedical Engineering & Imaging Sciences, King's College London, London, United Kingdom

Synopsis

Use of Multiband and high-TBW RF pulses in SSFP sequences is limited due to their long pulse duration and high RF energy. These two properties are not independent of each other, as shorter RF pulses lead to higher RF energy and often violate SAR limitations when using short repetition times (TR). We show how Time-optimal VERSE can be used to produce pulses that are optimized for minimum TR performance with both single and multi-band examples.

Purpose

Rapid gradient echo sequences are widely used for rapid MRI. Scan duration is directly proportional to the repetition time (TR), hence minimization of TR leads to direct reduction in scan duration, which is particularly important for cardiac imaging where such a reduction translates to reduced breathhold duration. For balanced SSFP an additional benefit is reduction in severity of banding artefacts. The situation is even more acute when using multi-band RF pulses for Simultaneous Multi-Slice acquisition, since the relatively long RF pulses with high energy (i.e. SAR) lead to long TR^1,2.

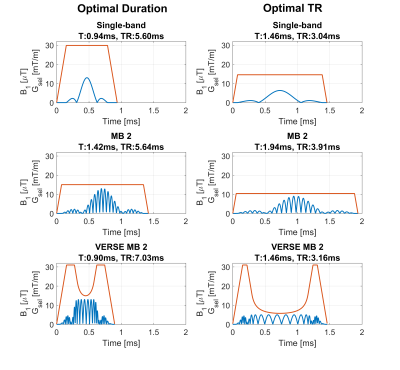
Much recent research into multi-band pulse design has focused on minimizing pulse durations, and one method for doing so is to use time-variable selection gradients, designed using Time-optimal VERSE³ or optimal control approaches⁴. However, the problem of minimizing RF pulse duration and minimizing TR are not equivalent because the minimum TR is often constrained by SAR, and shortening RF pulses increases their RF energy. This is illustrated in Figure 1.

In this work we reformulate the design problem as one of ‘minimum-TR’ rather than ‘minimum-duration’ using Time-optimal VERSE. A range of time-variable gradient pulses are considered including both multi-band and single-band designs.

Theory

Minimum TR optimization

The minimum TR of a sequence is a function of desired flip angle, time-bandwidth product and peak B1 amplitude. Different peak B1 amplitudes will result in different RF energy and pulse durations⁵. For an RF pulse with duration $$$\tau$$$ and energy $$$ E_{rf} = \int_{0}^{\tau}b_1(t)^2dt $$$ the minimum TR is given by: $$ TR_{min} = \frac{E_{rf}}{SAR_{max}} $$

Where $$$SAR_{max}$$$ is the maximum SAR. This relation becomes non-trivial for VERSE pulses since these are optimised for a particular $$$B_1$$$ amplitude and they change shape when re-designed for a different constraint.

Regardless of pulse design, minimum TR is also affected by the minimum necessary encoding time $$$t_{enc}$$$ and RF gating duty cycle $$$0<\delta_0<1$$$ $$TR_{min} = max\left\lbrace\tau + t_{enc}, \frac{\tau}{\delta_0}\right\rbrace$$

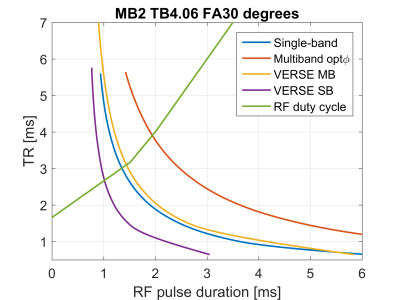
The optimal TR is found by designing RF pulses for a range of peak $$$B_1$$$ amplitudes, then selecting the minimum TR pulse which meets both conditions specified above. The process is illustrated by intersecting the curves shown on Figure 2.

Methods

RF pulse design

Vendor RF pulses with Time-bandwidth products 2 to 10 were scaled to flip angles 15 to 90 degrees. Time-optimal VERSE was applied to create VERSE SB pulses. Multiband pulses to excite 2,3 and 4 slices were created by applying a time-dilated Multi-band modulation function to the VERSE SB pulses. Normal multiband pulses were designed using real-only modulation⁵. The peak $$$B_1$$$ was varied from $$$1\mu T$$$ to $$$13\mu T$$$.

Minimum TR

The minimum TR was determined for local SAR limit = 20W/kg, RF duty cycle $$$\delta_0$$$= 0.5 and minimum encoding time $$$t_{enc}$$$= 1.66ms.

Results & Discussion

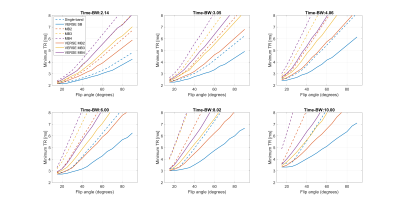
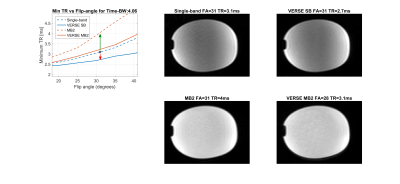
Figure 3 shows the minimum TR achievable for a range of Multiband factors, flip angles and time-bandwidth products. In all cases examined, VERSE could deliver a pulse shape which leads to a shorter TR than a conventional MB pulse. VERSE MB2 cases often come with only a small additional TR penalty compared to single-band cases, especially for time-bandwidth products 3.05 and 4.06. The largest benefit in relative TR reduction is seen at high time-bandwidth products, with some VERSE MB cases resulting in shorter TRs than their single-band equivalents. Figure 4 shows some examples of how the use of VERSE can either lead to a reduction in TR for the same flip angle (single band) or the addition of an extra slice (MB2 from single band) with no penalty in TR or a negligible loss in flip angle. Conversely, a conventional Multiband 2 pulse with the same flip-angle would require an increase of 1ms in TR.

Conclusion

By explicitly considering the hardware and safety related constraints we produced minimum-TR pulse designs for rapid gradient echo imaging. These designs are not always either the minimum duration or energy pulse, but fit optimally within the other existing trade-offs. Such an approach would also be suitable for bSSFP at high flip angle for improved cardiac imaging1,5, or quantitative MRI with high quality slice profile (high time-bandwidth product)⁷. Even at low time-bandwidth product an VERSE MB2 pulse can result in a TR comparable to a single-band equivalent. Moreover, as found in⁸, a higher slice quality can be used for marginal increase in TR.

Acknowledgements

This work was supported by the Wellcome EPSRC Centre for Medical Engineering at Kings College London (WT 203148/Z/16/Z), MRC strategic grant MR/K006355/1, King’s College London & Imperial College London EPSRC Centre for Doctoral Training in Medical Imaging (EP/L015226/1) and by the National Institute for Health Research (NIHR) Biomedical Research Centre based at Guy’s and St Thomas’ NHS Foundation Trust and King’s College London. The views expressed are those of the authors and not necessarily those of the NHS, the NIHR or the Department of Health. SJM acknowledges support from the EPSRC (EP/L00531X/1). The student stipend for SAS is partially funded by Philips Healthcare.

References

1. Wang Y, Shao X, Martin T, Moeller S, Yacoub E, Wang DJJ. Phase-cycled simultaneous multislice balanced SSFP imaging with CAIPIRINHA for efficient banding reduction. Magn. Reson. Med. 2016;76. doi: 10.1002/mrm.26076.

2. Price AN, Cordero-Grande L, Malik SJ, Hajnal J V. Accelerated Cine Imaging of the heart using Blipped Multiband SSFP. Proc. Intl. Soc. Mag. Reson. Med. 25 2017:631.

3. Lee D, Lustig M, Grissom WA, Pauly JM. Time-optimal design for multidimensional and parallel transmit variable-rate selective excitation. Magn. Reson. Med. 2009;61:1471–1479. doi: 10.1002/mrm.21950.

4. Aigner CS, Clason C, Rund A, Stollberger R. Efficient high-resolution RF pulse design applied to simultaneous multi-slice excitation. J. Magn. Reson. 2016;263:33–44. doi: 10.1016/j.jmr.2015.11.013.

5. Beqiri A, Price AN, Padormo F, Hajnal J V., Malik SJ. Extended RF shimming: Sequence-level parallel transmission optimization applied to steady-state free precession MRI of the heart. NMR Biomed. 2017;30:1–15. doi: 10.1002/nbm.3701.

6. Abo Seada S, Price AN, Hajnal J V., Malik SJ. Optimized amplitude modulated multiband RF pulse design. Magn. Reson. Med. 2017;0:1–9. doi: 10.1002/mrm.26610.

7. Ye H, Cauley SF, Gagoski B, Bilgic B, Ma D, Jiang Y, Du YP, Griswold MA, Wald LL, Setsompop K. Simultaneous multislice magnetic resonance fingerprinting (SMS-MRF) with direct-spiral slice-GRAPPA (ds-SG) reconstruction. Magn. Reson. Med. 2017;77:1966–1974. doi: 10.1002/mrm.26271.

8. B. A. Hargreaves, C. H. Cunningham, D. G. Nishimura, S. M. Conolly. Time-Optimal VERSE Excitation for 3D Balanced SSFP Imaging. Proc. 12th Annu. Meet. ISMRM 2004;11:260.

Figures

An illustration showing the distinction between minimum pulse duration (left column) and results for pulses which minimize TR (right column). Short RF pulses have higher RF energy, and can therefore violate SAR constraints in SSFP sequences with short TR. To optimize for minimal TR a pulse shape with a lower peak amplitude is preferable, and VERSE can help to achieve this. The optimization space for these pulses is shown in figure 2.

An example of how each method is optimized for minimum TR. Each point on the curve relates to an RF pulse designed for a different peak amplitude, which gives it a different pulse duration, a different RF energy, and thus a different TR value. The minimum TR achievable is dictated by the intersection of each method with the RF duty cycle. In this case, VERSE MB can result in a TR reduction of 0.75ms compared to a conventional MB pulse.

Minimum TR achievable for a range of flip-angles, for a range of RF pulses. Solid lines show VERSE methods, which always result in a lower TR than their constant gradient equivalents (dashed). VERSE MB2 pulses can result in almost equivalent TR as single-band pulses for Time-bandwidth product 3.05 and 4.06, and even outperforms it at higher time-bandwidth products.

Phantom experiments using optimal TR solutions to validate minimum TR calculations. A replicate of a subplot from Figure 3 is shown in the top left. As marked by the red arrow, VERSE SB can achieve a 15% reduction in TR without sacrificing on flip angle. Instead, for the same TR a VERSE MB2 pulse can be used. To do the same with conventional MB2, an increase of 1ms is necessary, as marked by the green arrow.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)

3403