Synopsis

This study investigates different parallel transmission (PTx) pulse design methods to find a universal PTx-pulse that excites the same local pattern with a 90 degree flip-angle across different heads. Thus, it abandons prospective the need for time-consuming subject specific B₁₊ mapping and PTx-pulse calculation, during the scan session. The best results were achieved by solving a minimax optimization problem were the maximum normalized root mean square error (NRMSE) over all subjects was minimized. The resulting pulse created magnetization profiles with a maximum NRMSE of around 0.049 across all volunteers.

Introduction

Parallel transmit (PTx) systems offer more flexibility for designing tailored RF-pulses. However, the process of PTx-pulse-design often includes measuring the B₁-field distribution for each transmit channel for each subject. In addition with the pulse calculation procedure, which is currently performed during the scan session, it leads to lengthy scan times and limits the performance of the PTx-applications.

Recently, Gras et al.¹ introduced the concept of ‘universal’ PTx-pulses, which does not require the knowledge of individual B₁ distribution, and rather relies on a pre-collected database. However, these studies only considered the case of low flip-angle whole-brain excitation pulses that mitigate B₁₊. In this study, we extend this method to local parallel transmit excitation pulses and investigate different possibilities to design a calibration-free ‘universal’ PTX-pulse which consistently excites the same local pattern across a single slice with a flip-angle of 90 degrees on different heads.

Methods

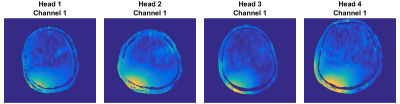
For four different heads of healthy volunteers the B₁-maps from each transmit channel of an 8-channel RF coil were measured (H1, H2, H3, H4, see Figure 1). The goal was then to find the best strategy to design a single pulse that would consistently excite the same local pattern on these four heads.

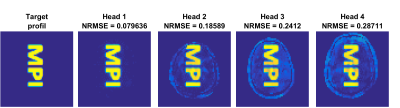
A local excitation pattern depicting the letters ‘MPI’ was chosen as the target excitation profile (see Figure 2, left). A 2D spiral k-space trajectory and a pulse duration of under 15ms was used for the pulse-design. B₀-field inhomogeneities, and T₁ , T₂ relaxation times were not considered during this simulation study.

Firstly, the pulse was calculated based on the B₁-maps acquired from the smallest head (H1) using an optimal control pulse-design method (GRAPE)^2,3. The H1-tailored pulse was used for excitation on all four volunteers. The resulting profiles were simulated using Bloch equations and their performance were compared. Afterwards, the same procedure was performed with a H4-tailored pulse.

Next, the individual B₁-maps measured on H1-4 were averaged on a pixel-wise basis to form an average B₁-map. The pulse was calculated based on this average B₁-map and evaluated on all four heads.

Lastly, a ‘universal’ local excitation pulse was designed following the method proposed by Gras et al¹. A minimax cost function (MinMaxCF) was used for the optimization, where at each step the normalized root mean square error (NRMSE) between the resulting magnetization profile and the target profile on all four heads is calculated and the maximum of these values is minimized with an active-set algorithm.

Results

As depicted in Figure 2, the pulse tailored on H1 shows excellent performance on H1 as expected. However, the performance degrades on other heads. For instance, there is a NMRSE of 0.186 when the H1-tailored pulse is used on H2. A similar trend can be seen in Figure 3, where the tailored pulse works for the head it was designed for (H4) but not for the other heads.

Figure 4 shows the performance of the pulse designed based on the average B1-map on all four volunteers. The performance of this pulse is on average better than the H1- or H4-tailored pulse. For instance, compared to a NMRSE of 0.186 for the H1-tailored pulse, and 0.221 for the H4-tailored pulse, the average pulse results in an NMRSE of 0.175 on H2.

Figure 5 shows the results from the pulse designed with the MinMaxCF method. The maximum NRMSE among all four heads for this pulse is 0.049 (on H4). This value is much better than all the NRMSE’s achieved before, even better than the NRMSE of the tailored pulses evaluated on the same corresponding single heads.

Discussion

A local excitation RF-pulse tailored to one head performs sub-optimally on different heads. This is especially true for the areas outside the local excitation patter (‘MPI’): significant excitation can be detected outside the letters, where ideally nothing should be excited. Marginal improvement was achieved by using the average B₁-map for pulse design, however the resulting magnetization profiles were still not optimal.

The best results were achieved by using the universal pulse calculated from the MinMaxCF optimization method. The NMRSE resulting from this pulse on all four heads was less than 0.049, which makes this pulse ‘universal’ for use on all four volunteers.

Conclusion

Acknowledgements

I want to thank Sahar Nassirpour for proofreading.

Funding by the European Union (ERC Starting Grant, SYNAPLAST MR, Grant Number: 679927) is gratefully acknowledged.

References

1. Gras V., Vignaud A., Le Bihan D., Boulant N. Universal Pulses: A New Concept for Calibration-Free Parallel Transmission. Magnetic Resonance in Medicine. 2017; 77:635-643

2. Xu D, King KF, Zhu Y, McKinnon GC, Liang Z- Designing multichannel, multidimensional, arbitrary flip angle RF pulses using an optimal control approach. Magnetic Resonance in Medicine. 2008; 59:547–560

3. Khaneja N., Reiss T., Kehlet C., Schulte-Herbruggen T., Glaser S.J. Optimal control of coupled spin dynamics: design of NMR pulse sequences by gradient ascent algorithms. Journal of Magnetic Resonance. 2005; 172:296–305