3391
A Simplified Framework for Contrast Optimization in MRI1CREATIS, Villeurbanne, France, 2Department of Chemistry, TUM, Munich, Germany, 3ICB, Dijon, France, 4TUM, Institute for Advanced Study, Munich, Germany
Synopsis
This abstract details the implementation and interest of an adapted parameterization for the computation of contrast preparation schemes in an optimal control framework. It optimally balances the effect of T1 and T2 relaxation, penalizes long preparation sequences in order to improve the compromise between contrast performance and preparation time, and significantly reduces the computation time. As an example, an in vitro experiment validates the contrast benefit over an inversion-recovery scheme. Finally, it offers a huge flexibility in terms of achievable contrasts, which is demonstrated in vivo by a white-matter enhancement experiment on a rat brain.
Introduction
The objective of contrast preparation sequences is to create a significant magnetization difference on the longitudinal axis before the excitation scheme. Standard methods typically use either T1[1] or T2[2,3] differences to create contrast. Parameter tuning can be performed through Bloch simulations, but in no way it guarantees the solution’s efficiency or that it cannot be improved. Recent research has focused on designing specific contrast preparation pulses that account for the global magnetization dynamics, i.e. both T1 and T2, to optimize the prepared contrast[4,5]. The generation of such pulses is performed using an optimal control framework, which incorporates both the global magnetization evolution and experimental variations[6]. Significant improvement was shown in the context of short-T2 enhancement. Computing such pulses can take several hours, and often results in highly non-trivial shapes which obscure the understanding of the underlying contrast mechanism. The present work proposes a new pulse parameterization to improve the efficiency of the design process. It is validated both in vitro and in vivo by creating a non-trivial white matter enhancement contrast in a rat brain.Methods
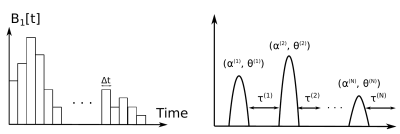
Numerical optimal control approaches often consider the complex amplitude of the pulse at each discrete time point as an optimization variable, which typically results in several thousands of variables. It is proposed to only consider a finite number (N=3) of block pulses, defined by their respective flip angle $$$\alpha^{(i)}$$$, phase $$$\theta^{(i)}$$$ and post-pulse delay $$$\tau^{(i)}$$$, resulting in only 9 optimization variables (Figure 1). The optimal control implementation is performed with GRAPE[5], which iteratively updates the optimization variables to decrease the following cost function:
$$\mathcal{C}^{a>b} = \Vert \overrightarrow{M^b}(T)\Vert-\Vert \overrightarrow{M^a}(T)\Vert + \gamma \sum_{i<N}\tau^{(i)} $$
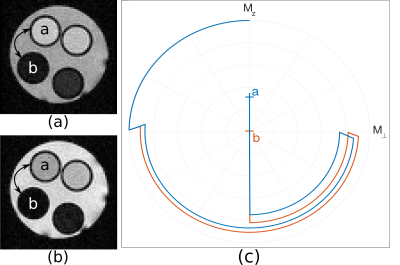
in which $$$ \overrightarrow{M^a}$$$ and $$$ \overrightarrow{M^b}$$$ are respectively the macroscopic magnetization vectors of samples a and b, whose evolution is ruled by Bloch equations ; $$$T$$$ is the total preparation time (with $$$T = \sum \tau^{(i)}$$$), and $$$\gamma$$$ is a scalar that balances the influence of the control time penalization term. This cost function reaches a minimum when the contrast between both samples is maximum (with $$$\Vert \overrightarrow{M^a}(T)\Vert > \Vert \overrightarrow{M^b}(T)\Vert $$$). Note that the proposed parameterization penalizes long pulse sequences via the control time regularization term, which optimizes the compromise between contrast and preparation time. The method is validated with two experiments carried out on a small-animal 4.7T Bruker MR system. The first experiment emphasizes the improvement of the compromise between preparation time and contrast performance. It consists in contrasting two in vitro samples: a and b, whose relaxation times are [T1a, T2a] = [247, 90] ms and [T1b, T2b] = [381, 131] ms. The objective is to maximize sample a over sample b, which would intuitively be achieved with an inversion recovery preparation because of the shorter T1 and T2 values of sample a. The second experiment validates the ability of the proposed method to perform in vivo short-T2 enhancement, by creating a non-trivial contrast between white and gray matter in a rat brain.
Results
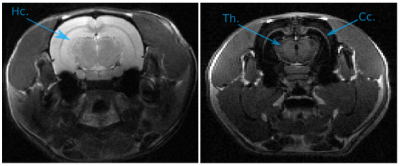
The drastic parameter reduction allows the computation of preparation schemes within a minute on a regular computer – where more than 20 hours were required with the scheme that optimizes the complex amplitudes at each time point. Figure 2 compares the image acquired with the proposed preparation scheme, versus an image acquired with an inversion recovery preparation of the same duration: $$$T$$$ = 256 ms. The optimized preparation sequence is: $$$90° \xrightarrow{13\,ms} 180° \xrightarrow{13\,ms} -90° \xrightarrow{230\,ms}$$$, which results in a contrast improvement of 14%. The improvement is explained by the fact that fast T2 decay initially creates significant signal difference in the transverse plane, before being flipped on the longitudinal axis where T1 accentuates the contrast (Figure 2c). This significantly accelerates the longitudinal recovery process. Note that the benefit will grow for longer T1 values. Figure 3 presents a short-T2 enhancement rat brain acquisition, in which the corpus callosum and the thalamus are clearly enhanced compared to surrounding tissues. The optimized preparation scheme is given by: $$$90° \xrightarrow{17.1\,ms} 180° \xrightarrow{17.1\,ms} -90° \xrightarrow{628.2\,ms}$$$.Conclusion & Discussion
This abstract details the implementation and interest of an adapted parameterization for the computation of contrast preparation sequences in an optimal control framework. It optimally balances the effect of T1 and T2 relaxation, penalizes long preparation sequences to improve the compromise between contrast performance and preparation time, and significantly reduces the computation time. It offers a huge flexibility in terms of achievable contrasts via the computation of specific preparation schemes. Finally, the use of block pulses in the optimized preparation scheme makes the method easily applicable on any MR system.Acknowledgements
This work is supported by the ANR-DFG research program Explosys (Grant No.ANR-14-CE35-0013-01; GL203/9-1), the Technische Universität München Institute for Advanced Study, the German Excellence Initiative, the E. U. Seventh Framework Program under Grant No. 291763, and the LABEX PRIMES (ANR-11-LABX-0063/ ANR-11-IDEX-0007). The authors would like to acknowledge support from the PILoT imaging platform, member of France Life Imaging network (grant ANR-11-INBS-0006).References
[1] J. V. Hajnal, B. De Coene, P. D. Lewis, C. J. Baudouin, F. M. Cowan, J. M. Pennock, I. R. Young, and G. M. Bydder. High signal regions in normal white matter shown by heavily T2-weighted CSF nulled IR sequences. Journal of computer assisted tomography, 16(4):506–513, 1992
[2] P. E. Z. Larson, P. T. Gurney, K. Nayak, G. E. Gold, J. M. Pauly, and D. G. Nishimura. Designing long-T2 suppression pulses for ultrashort echo-time imaging. Magnetic Resonance in Medicine, 56(1):94–103, 2006
[3] M. Weiger, M. Wu, M. C. Wurnig, D. Kenkel, A. Boss, G. Andreisek, and K. P. Pruessmann. ZTE imaging with long-T2 suppression. NMR in Biomedicine, 28(2):247–254, 2015
[4] M. Lapert, Y. Zhang, M. Janich, S. J. Glaser and D. Sugny. Exploring the physical limits of saturation contrast in Magnetic Resonance Imaging. Sci. Rep. 2, 589, 2012
[5] E. Van Reeth, H. Ratiney, M. Tesch, D. Grenier, O. Beuf, S. J. Glaser, and D. Sugny. Optimal control design of preparation pulses for contrast optimization in MRI. Journal of Magnetic Resonance, 279:39 – 50, 2017
[6] N. Khaneja, T. Reiss, C. Kehlet, T. Schulte-Herbrüggen, and S. J. Glaser. Optimal control of coupled spin dynamics: design of NMR pulse sequences by gradient ascent algorithms. Journal of Magnetic Resonance, 172(2):296– 305, 2005
Figures