Synopsis

Two different transmit B₁⁺ mapping techniques were implemented and investigated for cardiac B₁⁺ shimming at 3T: (1) 2D cardiac-triggered spiral-Bloch-Siegert B₁⁺ mapping; (2) 3D Zero-Echo-Time (ZTE) B₁⁺ phase mapping. B₁⁺ homogeneity was optimised and performance assessed by evaluating the cardiac black-blood fast spin-echo sequence performance in healthy volunteers.

Introduction

Methods

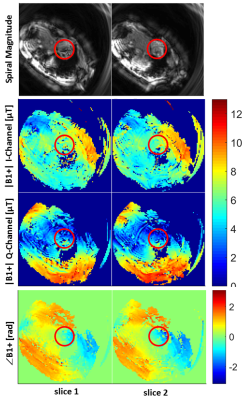
The spiral-Bloch-Siegert method is based on rapid spiral imaging with transmit magnitude |B₁⁺|-mapping using the phase-sensitive Bloch-Siegert method [1]. Four spiral arms are used to encode one image (matrix size=100², FOV=(40cm)², spiral arm t=8.9ms; Bloch-Siegert pulse t=4ms, f_off=2kHz), requiring two repetitions for plus-minus the Bloch-Siegert frequency, and another two for the two transmit channels I and Q (4×2×2=16 excitations in total). One excitation and encoding takes 52.4ms (due to SAR constraints), hence the whole scan can be acquired with cardiac gating in a single breath-hold and with multiple slices. The transmit RF phase map ($$$\angle$$$B₁⁺) is extracted from the coil-combined phase difference between the two transmit channels.

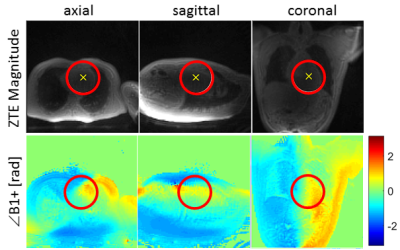
The Zero-Echo-Time (ZTE) B₁⁺ phase mapping method is based on measuring a low-resolution 3D-radial ZTE image and extracting the phase difference map ($$$\angle$$$B₁⁺) between the two transmit channels scan (matrix size=100³, FOV=(40cm)³, scan duration=27s). The validity of using only the transmit RF phase map ($$$\angle$$$B₁⁺) for B1 shimming assumes sufficiently flat |B₁⁺| magnitudes of the two channels over the region-of-interest. Thus, B₁⁺ inhomogeneities are mainly caused by spatially varying transmit RF phase.

The goal of the subsequent B₁⁺ optimisation is to combine the two transmit channels optimising B₁⁺ homogeneity over the specified region of interest. The cost function is given by $$$\sum(f-\bar f)^2$$$ with $$$f=|B_I+wB_Q|$$$, $$$B_I$$$ and $$$B_Q$$$ denoting the two transmit channels I and Q combined with the complex weight $$$w=10^{-txAtten/200} \cdot \exp(i\cdot txPhase)$$$. txAtten is constrained by the system configuration to 0...45[dB/10], while txPhase to -45°...0°.

Both sequences were implemented on a 3T GE MR750w scanner including transmit-channel selection for an easy workflow. Seven healthy volunteers were examined (2 with spiral-Bloch-Siegert, 6 with ZTE B₁⁺ phase-mapping; body weights 60-95kg). All reconstruction, post-processing and B₁⁺ optimisation was implemented in Matlab.

Results and Discussion

The |B₁⁺| magnitude images measured with the spiral-Bloch-Siegert method (Fig. 1) are relatively flat within the region-of-interest, hence supporting the assumption that $$$\angle$$$B₁⁺ phase maps are sufficient for cardiac B₁⁺ optimisation. A typical ZTE $$$\angle$$$B₁⁺ phase map is shown in Fig. 2. While spiral-Bloch-Siegert yields full B₁⁺ magnitude and phase information, it is offset by a cumbersome measurement procedure, requiring cardiac gating, breath-hold, good shim, slice planning and yields only (multi-slice) 2D maps with limited robustness. ZTE is much simpler and more robust due to short TE and 3D radial properties of high oversampling and averaging in the centre of k-space, although ZTE is lacking |B₁⁺|-information.

The B₁⁺ optimisation generally yields the same results for both B₁⁺ mapping methods: maximum attenuating of one channel (txAtten=45[db/10]), while using the same phase as for quadrature mode (txPhase=0°). Note, that phase-based B1+ shimming relies on the assumption of flat |B₁⁺| I and Q magnitudes, which means a single channel has already optimal |B₁⁺| homogeneity. The theoretically optimal solution would therefore be to completely switch off one channel, hence eliminating the perturbing effects of $$$\angle$$$B₁⁺. As this would require doubling the power of the remaining channel, the system limits attenuation to a maximum of 45[dB/10].

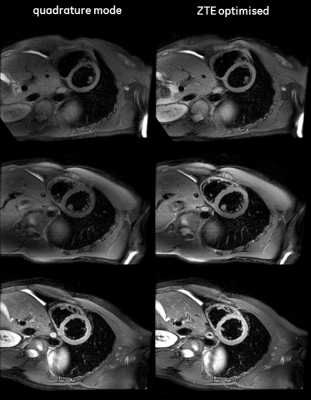
Fast-spin-echo images measured with standard quadrature mode and the optimised dual-drive values are shown in Fig. 3.

The B₁⁺ shimming results in the heart are reproducible and encouraging in the measured subjects, and further scans to confirm these initial findings are ongoing. The ZTE phase method may be applicable to other body regions as well, if the assumption of flat |B₁⁺| with the region-of-interest holds.

Acknowledgements

References

1. B1 mapping by Bloch-Siegert shift. Sacolick LI, Wiesinger F, Hancu I, Vogel MW. Magn Reson Med. 2010 May;63(5):1315-22. doi: 10.1002/mrm.22357.