Synopsis

Learning from existing datasets has the potential to improve reconstruction quality. However, deep learning based methods typically require many clean fully-sampled datasets as ground truths. Such datasets can be hard to come by, especially in applications where rapid scans are desired. Here, we propose a method based on convolutional sparse coding that can learn a convolutional dictionary from under-sampled datasets for sparse reconstruction. Recent works have shown close connections between deep learning and convolutional sparse coding. The benefit of convolutional sparse coding is that it has a well-defined forward model, and can be easily extended to incorporate physical models during training. We extend convolutional sparse coding to incorporate the under-sampling forward model. We show that the dictionary learned from under-sampled datasets is similar to the dictionary learned from fully-sampled datasets, and improves upon wavelet transform for l1 regularized reconstruction in terms of mean-squared error.

Introduction

Learning from existing datasets has the potential to improve reconstruction quality. However, deep learning based methods^1-4 typically require fully-sampled datasets with high signal-to-noise as ground truths in training. In many applications, clean fully-sampled raw datasets are scarce. Especially in applications where rapid scans are desired, a large number of fully-sampled datasets is infeasible to obtain. Noisy under-sampled datasets, on the other hand, can potentially be routinely acquired with parallel imaging and/or compressed sensing, and much easier to obtain in large numbers. The ability to learn from noisy undersampled k-space datasets is desirable.

Here, we propose a method based on convolutional sparse coding⁵ that can learn a convolutional dictionary from under-sampled datasets at large scale to improve sparse reconstruction. Recent works^5-6 have shown close connections between deep learning and convolutional sparse coding. The benefit of convolutional sparse coding is that it has a well-defined forward model, and can incorporate physical models during training. Through experiments, we show that we can learn effective dictionary from under-sampled datasets, which improves upon wavelet transform for $$$\ell1$$$-regularized reconstruction in terms of mean-squared error.

Theory

Convolutional Sparse Coding

Convolutional sparse coding⁵ was proposed to learn a dictionary of filters to provide sparse representations. As shown by several works^5-6, deep learning can be interpreted as layered versions of convolutional sparse coding. Convolutional sparse coding has the advantage of having an explicit forward model, enabling us to incorporate imaging models of training data.

Concretely, given images $$$\{x_i\}_{i=1}^m$$$, convolutional sparse coding seeks to represent them as sums of sparse coefficient images $$$\{\{\alpha_{ij}\}_{j=1}^n\}_{i=1}^m$$$ convolved with dictionary filters $$$\{d_j\}_{j=1}^n$$$:

$$x_i=\sum_{j=1}^nd_j\ast\alpha_{ij}$$

k-space Aware Convolutional Sparse Coding

We proposed k-space aware convolutional sparse coding to incorporate the forward model during training in order to learn from under-sampled datasets. Given k-space datasets $$$\{y_i\}_{i=1}^m$$$, and their corresponding forward operators$$$\{A_i\}_{i=1}^m$$$, which incorporates multi-channel sensitivity maps and under-sampling masks, we consider the following objective function for training:

$$\min_{\alpha_{ij},d_j:\|d\|_2\le1}\frac{1}{2m}\sum_{i=1}^m\left\|A_i\left(\sum_{j=1}^nd_j\ast\alpha_{ij}\right)-y_i\right\|_2^2+\lambda\|\alpha_{ij}\|_1$$

which allows us to learn filters $$$\{d_j\}_{j=1}^n$$$ from under-sampled k-space measurements, with sparse coefficients $$$\alpha_{ij}$$$.

Training

Training can be performed using stochastic alternating minimization. For each iteration, we randomly select a dataset with index $$$r$$$, and alternate between sparse reconstruction and dictionary update:

$$\alpha_{rj}=\underset{\alpha_{rj}}{\text{argmin}}\frac{1}{2}\left\|A_r\left(\sum_{j=1}^nd_j\ast\alpha_{rj}\right)-y_r\right\|_2^2+\lambda\|\alpha_{rj}\|_1$$

$$d_j=\underset{d_j:\|d\|_2\le1}{\text{argmin}}\frac{1}{2}\left\|A_r\left(\sum_{j=1}^nd_j\ast\alpha_{rj}\right)-y_r\right\|_2^2$$

Each sub-problem is a convex problem, and can be solved using FISTA⁸.

Reconstruction

Reconstruction is performed by solving the $$$\ell1$$$-regularized reconstruction:

$$\min_{\alpha_j}\frac{1}{2}\left\|A\left(\sum_{j=1}^nd_j\ast\alpha_{j}\right)-y\right\|_2^2+\lambda\|\alpha_{j}\|_1$$

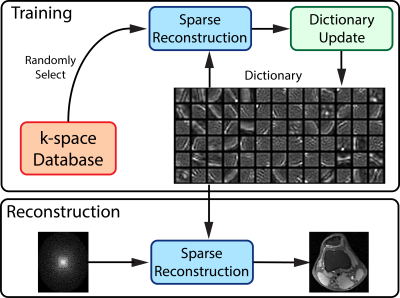
Figure 1 shows a graphical illustration of the training and reconstruction processes.

Methods

We trained, and evaluated the proposed method, implemented in Tensorflow, on 20 fully sampled 3D knee datasets⁷, publicly available on mridata.org. The k-space datasets were acquired on a 3T GE Discovery MR 750, with an 8-channel HD knee coil. Scan parameters include a matrix size of 320x320x256, and TE/TR of 25ms/1550ms.

A total of 5120 slices from 16 cases were used for training, 640 slices from 2 cases were used for validation, and 640 slices from the remaining 2 cases were used for testing. The datasets were normalized with respect to the maximum value of each 3D volume.

Using the proposed method, we first trained a dictionary from the fully-sampled training datasets, with 256 11x11 filters. We then under-sampled each 3D dataset with a different 8x Poisson-disk sampling mask with 24x24 calibration region. Using sensitivity maps estimated with ESPIRiT⁸, we trained another dictionary from under-sampled datasets. Regularization parameters were selected to minimize mean squared error in the validation datasets. We compared $$$\ell1$$$ reconstructions with the learned dictionaries and wavelet transform on the testing datasets.

Results

Figure 2 shows the convolutional dictionaries learned from fully-sampled and under-sampled datasets. Visually, the dictionaries show similar structures, indicating that the k-space aware convolutional sparse coding can learn effective dictionary from under-sampled datasets. Since the dictionaries were trained on spin-echo images, the phase is largely constant, with most variations coming from zero-crossings.

Figure 3 shows examples of the filters learned from the under-sampled datasets and their corresponding sparse coefficient images on a testing image.

Figure 4 shows a representative comparison of $$$\ell1$$$-regularized reconstructions with wavelet transform, and the learned dictionaries. In general, reconstructions with the dictionaries showed sharper edges, but slight noise amplifications as well. Over the 640 test slices, reconstruction with the dictionary learned from fully-sampled datasets increases the average PSNR by 0.168 dB compared with $$$\ell1$$$-wavelet reconstruction, and reconstruction with the dictionary learned from under-sampled datasets increases the average PSNR by 0.322 dB. A boxplot of the PSNR differences is shown in Figure 5. These show that the dictionary learned from under-sampled datasets can be used to improve compressed sensing reconstruction.

Conclusion

Acknowledgements

References

[1] Hammernik, Kerstin, et al. "Learning a Variational Network for Reconstruction of Accelerated MRI Data." arXiv preprint arXiv:1704.00447 (2017).

[2] Wang S, Su Z, Ying L, Peng X, Zhu S, Liang F, Feng D, Liang D. Accelerating Magnetic Resonance Imaging Via Deep Learning. In IEEE International Symposium on Biomedical Imaging (ISBI). 2016; 514–517.

[3] Yang Y, Sun J, Li H, Xu Z. Deep ADMM-Net for Compressive Sensing MRI. In Advances in Neural Information Processing Systems (NIPS). 2016; 10–18.

[4] Lee, Dongwook, Jaejun Yoo, and Jong Chul Ye. "Deep artifact learning for compressed sensing and parallel MRI." arXiv preprint arXiv:1703.01120(2017).

[5] Zeiler, Matthew D., et al. "Deconvolutional networks." Computer Vision and Pattern Recognition (CVPR), 2010 IEEE Conference on. IEEE, 2010.

[6] Papyan, Vardan, Yaniv Romano, and Michael Elad. "Convolutional Neural Networks Analyzed via Convolutional Sparse Coding." arXiv preprint arXiv:1607.08194 (2016).

[7] Epperson K, Sawyer AM, Lustig M, Alley M, Uecker M. Creation Of Fully Sampled MR Data Repository For Compressed Sensing Of The Knee. In: Proceedings of the 22nd Annual Meeting for Section for Magnetic Resonance Technologists, Salt Lake City, Utah, USA, 2013.

[8] Uecker, M., Lai, P., Murphy, M.J., Virtue, P., Elad, M., Pauly, J.M., Vasanawala, S.S. and Lustig, M., 2014. ESPIRiT—an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA. Magnetic resonance in medicine, 71(3), pp.990-1001.