3374

Combining MR-Physics and Machine Learning to Address Intractable Reconstruction Problems

Berkin Bilgic¹, Stephen F Cauley¹, Itthi Chatnuntawech², Mary Kate Manhard¹, Fuyixue Wang¹, Melissa Haskell¹, Congyu Liao¹, Lawrence L Wald¹, and Kawin Setsompop¹

¹Martinos Center for Biomedical Imaging, Charlestown, MA, United States, ²National Nanotechnology Center, Pathum Thani, Thailand

Synopsis

We are combining Machine Learning (ML) with MR-physics based image reconstruction to tackle intractable problems. We address open problems that are either too stochastic to be modeled (e.g. shot-to-shot phase variations in multi-shot EPI due to physiological noise), or that admit a computationally prohibitive model (e.g. motion correction with simultaneous estimation of motion parameters and image content). Using ML to jumpstart physics-based non-convex reconstructions dramatically improve their efficiency and helps avoid local minima. In return, MR-physics reconstruction keeps ML in check, and avoids using it as a blackbox. Such synergistic combination also provides >2x reduction in RMSE over conventional reconstruction.

Introduction

We are proposing to use ML to solve difficult problems in MR. These problems are either impossible to model (e.g. physiological/thermal noise), or there is a model (e.g. motion) whose solution is computationally infeasible. Rather than treating ML as a black-box, we are using it to jumpstart MR-physics based non-convex reconstructions, which would otherwise be computationally prohibitive and/or stuck at local minima. This allows us to simultaneously harness ML and sensitivity encoding.

We demonstrate that combined ML and MR-physics approach can address: i) patient motion, ii) shot-to-shot phase variations that obstruct Multi-Shot EPI (msEPI) reconstruction, and iii) noise in high-resolution diffusion acquisition.

Data/code: http://bit.ly/2y1xK65

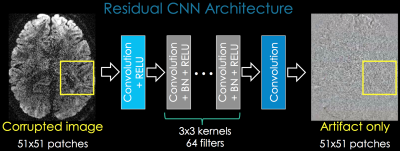
ML Reconstruction via Residual Convolutional Neural Networks (CNN)

Rather than estimating the artifact-free image, we learn the mapping between the corrupted image and the artifacts. Optimization for residual mapping is easier, allowing deeper networks with improved accuracy. We employ Residual CNN [1,2] [Fig1] with a patch-based approach. L1-loss and ADAM optimizer [3] were used in Keras running on a Titan-XP GPU.

i) Motion Correction with Residual CNN and TAMER

To enable efficient motion correction without navigators for RARE/TSE acquisition, we trained a residual network to correct for motion between shots.

Acquisition: in vivo TSE without motion, 2mm in-plane resolution, matrix=128x128, TE/TR=98/6100ms at Turbo-Factor=4 (32-shots).

Training: motion trajectories measured on 20 Alzheimer's patients were utilized to simulate artifacts. A 27-layer CNN learned the mapping between corrupted images and simulated motion artifacts.

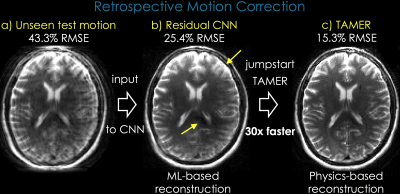
Reconstruction: The network was applied to an unseen motion [Fig2a, 43.3%RMSE], which substantially reduced artifacts [Fig2b, 25.4%RMSE]. This cleaner image provided an initial guess of motion parameters to jumpstart TAMER [4], an MR-physics based reconstruction that simultaneously solves for motion parameters and clean image:

$$min_{A_t,x}\sum_t{||F_t C A_t x - k_t||_2}^2$$

where $$$A_t$$$ is an affine motion transformation for shot $$$t$$$, $$$F_t$$$ is the undersampled DFT for this shot, $$$C$$$ are coil sensitivities, $$$x$$$ is the unknown image and $$$k_t$$$ is the k-space of shot $$$t$$$. TAMER solves this difficult non-convex problem by alternating between motion and image estimation, and computation takes hours. By initializing TAMER with Residual CNN, we accelerated the computation >30-fold, and cleaned up the remaining artifacts [Fig2c, 15.3%RMSE].

ii) Multi-shot Multi-contrast EPI: mitigating physiological noise with Residual CNN and Joint Reconstruction

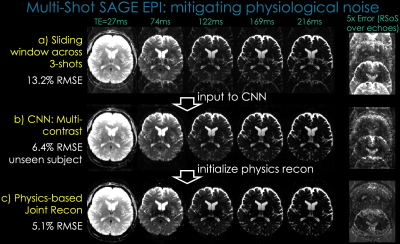
MS-EPI allows high-resolution acquisition with reduced distortion, but combining shots is prohibitively difficult because of shot-to-shot physiological phase variations, particularly in GE-EPI with long TE [Fig3a]. These variations may be mitigated using navigators, at the cost of imaging efficiency and in many cases, significant remaining artifacts. We obviate the need for navigators that reduce efficiency, and demonstrate spin-and-gradient-echo (SAGE [5]) msEPI.

Acquisition: Four volunteers were scanned using SAGE msEPI with 3-shots (FOV=220x220x149mm³, mtx=142x142x48, TEs=27/74/122/169/216ms, TR=12.6sec).

Training: Data from three volunteers were used for training a multi-contrast 25-layer network. Sliding-window combination of shots was used as corrupted input, and GRAPPA [6] reconstruction was used as the clean target. While GRAPPA can produce clean targets at 3-fold acceleration, in future we are targeting >10x undersampling per shot, which is beyond the capability of standard pRx.

Reconstruction: Sliding-window reconstruction of test subject [Fig3a, 13.2%RMSE] was processed with CNN to mitigate the artifacts [Fig3b, 6.4%RMSE]. To further clean up the artifacts, we propose a physics-based Joint Reconstruction. We fix the CNN magnitude $$$m_{cnn}$$$, and solve for the phase of each shot $$$\phi_t$$$ using phase-regularized reconstruction [7]:

$$min_{\phi_t}{||F_t C e^{i\phi_t} m_{cnn} - k_t||_2}^2 $$

Once we have the phase of each shot, we jointly solve for the magnitude $$$m_{joint}$$$ using data from all shots:

$$min_{m_{joint}}\sum_t{||F_t C e^{i\phi_t} m_{joint} - k_t||_2}^2$$

This further refines the reconstruction [Fig3c, 5.1%RMSE].

iii) Denoising ultra high-resolution gSlider-SMS diffusion acquisition

gSlider-SMS allows high-resolution diffusion imaging through simultaneous multi-slab acquisition with RF slab-encoding [8]. Despite using Connectome scanner and 64-channel coil [9], achieving submillimeter resolution with high-SNR is encoding-intensive, requiring multiple averages and long scans. We use ML to mitigate thermal noise, thereby improving SNR and reducing scan times.

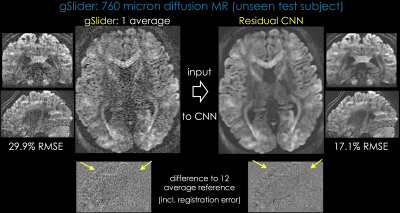
Acquisition: Two volunteers were scanned at 760μm isotropic resolution (mtx=290x210x176, TE/TR=82/5000ms) to collect 12-averages of b=2500s/mm² data.

Reconstruction: averages were registered using FLIRT [10], and 12-average data were used as the clean target. A 20-layer network was trained on one subject, and applied to another. Compared to single-average data which had 29.9%RMSE [Fig4], CNN had 17.1% error, similar to 3-averages of gSlider (15.9%RMSE).

Discussion and Conclusion

We combined ML with MR-physics to provide >2x RMSE reduction over conventional reconstruction, and substantial computation efficiency when modeling is impossible/impractical. This synergistic combination removed the black-box application of ML, and allowed MR-physics to keep ML in check. In return, ML facilitated the solution of non-convex, difficult physics-driven reconstruction problems.

This way, CNN+TAMER performs rapid motion correction without navigators, and CNN+msEPI will allow artifact-free, ultra-fast acquisition with low distortion. CNN+gSlider enjoys ~3-fold increase in SNR, enabling faster submillimeter diffusion scans.

Acknowledgements

We gratefully acknowledge support from NIH NINDS U01EB02516201, R24MH10609603 and NIBIB R01EB02061302, R01EB01733704.

References

1. Zhang K, Zuo W, Chen Y, Meng D, Zhang L. Beyond a Gaussian Denoiser: Residual Learning of Deep CNN for Image Denoising. IEEE Trans. Image Process. 2017;26:3142–3155. doi: 10.1109/TIP.2017.2662206.

2. Ioffe S, Szegedy C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. Int. Conf. Mach. Learn. 2015:448–456.

3. Kingma D, Ba J. Adam: A method for stochastic optimization. arXiv Prepr. 2014:arXiv:1412.6980.

4. Haskell M, Cauley SF, Wald LL. TArgeted Motion Estimation and Reduction (TAMER): Data Consistency Based Motion Mitigation Using a Reduced Model Joint Optimization. In: Proceedings of the 24th Annual Meeting ISMRM. ; 2016. p. 1849.

5. Schmiedeskamp H, Straka M, Newbould RD, Zaharchuk G, Andre JB, Olivot J-M, Moseley ME, Albers GW, Bammer R. Combined spin- and gradient-echo perfusion-weighted imaging. Magn. Reson. Med. 2012;68:30–40. doi: 10.1002/mrm.23195.

6. Griswold MA, Jakob PM, Heidemann RM, Nittka M, Jellus V, Wang J, Kiefer B, Haase A. Generalized autocalibrating partially parallel acquisitions (GRAPPA). Magn. Reson. Med. 2002;47:1202–1210. doi: 10.1002/mrm.10171.

7. Ong F, Cheng J, Lustig M. General Phase Regularized Reconstruction using Phase Cycling. arXiv Prepr. 2017:arXiv:1709.05374.

8. Setsompop K, Fan Q, Stockmann J, et al. High-resolution in vivo diffusion imaging of the human brain with generalized slice dithered enhanced resolution: Simultaneous multislice (gSlider-SMS). Magn. Reson. Med. 2017. doi: 10.1002/mrm.26653.

9. Keil B, Blau JN, Biber S, Hoecht P, Tountcheva V, Setsompop K, Triantafyllou C, Wald LL. A 64-channel 3T array coil for accelerated brain MRI. Magn. Reson. Med. 2013;70:248–258. doi: 10.1002/mrm.24427.

10. Jenkinson M, Bannister PR, Brady M, Smith SM. Improved Optimization for the Robust and Accurate Linear Registration and Motion Correction of Brain Images. Neuroimage 2002;17:825–841. doi: 10.1006/NIMG.2002.1132.

Figures

Rather than learning the original mapping between clean and corrupted data, we learn the residual relation between the corrupted and artifact-only images. The Residual CNN architecture is simple, consisting of convolutional layers, batchNormalization (BN, for faster training and improved performance) and RELU nonlinearities. Middle layers employ 3x3 kernels with 64 filters. We follow a patch-based approach where we slide 51x51 windows across the image and average the network outputs in each voxel.

Residual CNN trained on Alzheimer's patient data allows substantial motion artifact reduction when applied to an unseen test motion. There are however minor remaining artifacts (yellow arrows). We use this interim CNN reconstruction to jumpstart MR-physics based TAMER algorithm, which uses the extra degrees of freedom in coil sensitivities to simultaneously estimate motion parameters and the clean image. This non-convex problem is difficult to solve and normally takes hours. With the CNN initialization, the optimization can be performed 30-fold faster, and the remaining artifacts are eliminated.

Sliding window reconstruction across 3-shots of multi-contrast, multi-shot EPI leads to substantial artifacts (13.2%RMSE) due to shot-to-shot physiological phase differences. These are largely mitigated using multi-contrast Residual CNN (6.4%RMSE) for this unseen test dataset. We use the CNN result to initialize our MR-physics based Joint Reconstruction: given the CNN magnitude, we estimate the phase of each shot. With these phase estimates, we then jointly solve for the magnitude image with data from all 3-shots. This leads to further improvement (5.1%RMSE) over the CNN reconstruction.

Residual CNN provides substantial SNR improvement for gSlider-SMS diffusion acquisition at 760um isotropic resolution. Despite exploiting cutting-edge hardware (Connectome scanner and 64-channel custom head-coil) and volumetric noise averaging benefit of gSlider, achieving such high-resolution with high-SNR is very encoding intensive. Residual CNN reconstruction has similar error as 3-averages of gSlider acquisition (17.1% vs 15.9%), indicating a near 3-fold improvement in SNR-efficiency. We note that the structured artifacts (yellow arrows) in both 1-average gSlider and CNN reconstructions are in part due to imperfect registration between individual averages in the 12-average ground truth data.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)

3374