3369

Highly-Scalable Image Reconstruction using Deep Neural Networks with Bandpass Filtering
Joseph Yitan Cheng1, Feiyu Chen2, Marcus T. Alley1, John M. Pauly2, and Shreyas S. Vasanawala1

1Radiology, Stanford University, Stanford, CA, United States, 2Electrical Engineering, Stanford University, Stanford, CA, United States

Synopsis

To increase the flexibility and scalability of deep convolution neural networks in the context of MRI reconstruction, a framework is proposed using bandpass filtering. The introduction of bandpass filtering enables us to leverage imaging physics while ensuring that the final reconstruction is consistent with known measurements to maintain diagnostic accuracy. We demonstrate this architecture for reconstructing subsampled datasets of contrast-enhanced T1-weighted volumetric scans of the abdomen. Additionally, we demonstrate the generality of the framework through the reconstruction of wave-encoded 2D single-shot fast-spin-echo scans of the abdomen. The proposed technique performs comparably with state-of-the-art techniques while offering the ability for simple parallelization and increase computational speed.

Introduction

Deep convolutional neural network (ConvNet) is a powerfully flexible tool. A major advantage is that conventional ConvNets can be applied on a patch by patch basis in the image domain. This feature allows these networks to be extremely flexible and highly scalable for images of arbitrary dimensions. However, for MRI reconstruction, the scalability and flexibility of these ConvNets are lost if we aim to exploit known k-space properties. Thus, we developed an infrastructure to enable highly-scalable MRI reconstruction using ConvNets. We demonstrate this architecture for accelerated imaging.

Methods

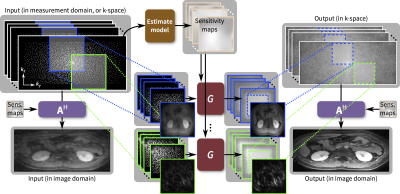
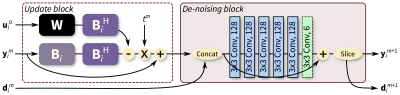
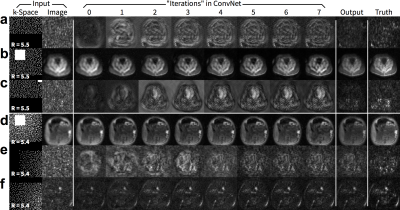
We propose to train and apply ConvNets on patches of k-space data (Figure 1). More specifically, a bandpass filter is used to isolate the reconstruction to small localized patches in k-space. With contiguous k-space patches, the ability to exploit and enforce the data acquisition model1,2 is maintained. For each patch, the inverse problem of estimating missing data samples is solved using an unrolled ConvNet architecture3–6. Here, we developed a ConvNet based on the iterative soft-shrinkage algorithm (ISTA) as illustrated in Figure 2. The final network consists of 8 “iterations” of ISTA with trainable step sizes and convolutional weights. Example input and output for select bands of k-space are shown in Figure 3. The phase induced by the off-center bandpass filtering is modeled to simplify the de-noising operation. A low-resolution image and the location of the k-space patch are included as additional inputs. The bandpass filtering was designed for 64x64 patches, and the final image is reconstructed by averaging the results from overlapping patches.

With IRB approval, gadolinium-contrast-enhanced T1-weighted volumetric abdominal scans were acquired on GE MR750 3T scanners using intrinsic navigation7 and modest subsampling $$$(R=1.2–2)$$$. Raw data were coil-compressed8 to 6 coils, and images were first reconstructed using soft-gated9,10 compressed-sensing-based parallel imaging with L1-ESPIRiT2. The Cartesian scans were separated into individual $$$x$$$-slices, and subsampling was performed in the $$$(k_y,k_z)$$$-plane. This dataset consisted of 229, 14, and 58 pediatric subjects (44006, 2688, and 11136 slices) for training, validation, and testing, respectively. Uniform and variable-density poisson-disc subsampling were used $$$(R=2–9)$$$.

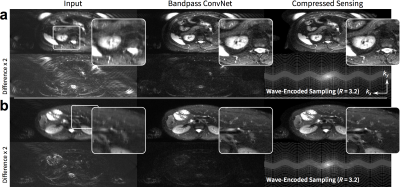
To demonstrate the generality of the approach, we adapted the imaging model to consider non-Cartesian trajectories: the imaging model included sampling along the non-Cartesian trajectories. T2-weighted 2D wave-encoded11–13 single-shot fast-spin-echo 3T scans were acquired with variable-density subsampling $$$(R=3.2)$$$. Raw data were coil compressed8 to 18 coils. Due to T2 decay and patient motion, fully sampled datasets cannot be obtained; thus, L1-ESPIRiT reconstruction was considered as ground truth. This dataset consisted of 104, 8, and 25 subjects (5005, 383, and 1231 slices) for training, validation, and testing, respectively.

The ISTA-based ConvNet was implemented with and without the proposed bandpass filtering in TensorFlow14. Comparison L1-ESPIRiT reconstructions and the generation of subsampling masks were performed using BART15. Images were evaluated with peak-signal-to-noise-ratio (PSNR), root-mean-square-error normalized by the norm of the reference (NRMSE), and structural-similarity metric16 (SSIM).

Results

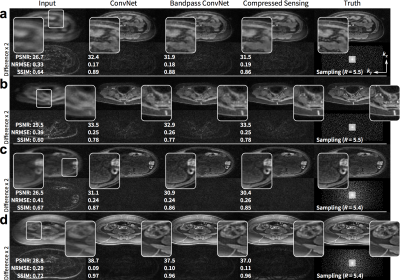
The proposed approach performed comparably with the full ConvNet and with L1-ESPIRiT with metric values within a standard deviation. For the T1-weighted dataset, the uniformly subsampled ($$$R=5.5$$$) input had an average (±standard deviation) of PSNR=29.4±2.4, NRMSE=0.33±0.08, and SSIM=0.68±0.07. ConvNet with no bandpass filtering had PSNR=34.9±3.6, NRMSE=0.18±0.06, and SSIM=0.87±0.06. The proposed approach had PSNR=34.7±3.2, NRMSE=0.19±0.06, and SSIM=0.87±0.06. L1-ESPIRiT had PSNR=35.4±3.7, NRMSE=0.17±0.07, and SSIM=0.87±0.06. Similar trend was observed with variable-density subsampling ($$$R=5.4$$$). The difference images with ground truth had no apparent structure (Figure 4), indicating no loss of anatomical features. Similarly, for the test wave-encoded dataset, the proposed ConvNet had comparable results to L1-ESPIRiT (Figure 5).

Discussion

The parallelization of conventional reconstruction algorithms is limited by the need to reconstruct the entire k-space together. Here, we demonstrated the ability to truly parallelize the entire reconstruction by separating the process into k-space patches. As a result, the reconstruction can be performed in a hybrid bandpass-filtered space that can exploit unique properties of image sparsity and data consistency.

With the proposed approach, the input data dimensions into the ConvNets are reduced which decreases memory footprint and increases computational speed for training and inference. For a 256x256 image reconstructed with 64x64 patches, the proposed approach offers over 28x less operations for each Fourier transform. Our approach enables the processing of high-dimensional (>256) and multi-dimensional (3+) images. Thus, possible resolutions and data dimensions does not need to be limited by the computation hardware or the acceptable computation duration for high-speed imaging applications.

This highly-scalable ConvNet was demonstrated for accelerated imaging reconstructions of Cartesian and wave-encoded acquisitions. This approach can be easily extended to other trajectories and other imaging models to fully leverage the capabilities of deep learning for MRI.

Acknowledgements

NIH R01-EB009690, NIH R01-EB019241, and GE Healthcare.

References

  1. Pruessmann, K. P., Weiger, M., Scheidegger, M. B. & Boesiger, P. SENSE: sensitivity encoding for fast MRI. Magn. Reson. Med. 42, 952–962 (1999).
  2. Uecker, M. et al. ESPIRiT-an eigenvalue approach to autocalibrating parallel MRI: Where SENSE meets GRAPPA. Magn. Reson. Med. 71, 990–1001 (2014).
  3. Hammernik, K. et al. Learning a Variational Network for Reconstruction of Accelerated MRI Data. arXiv: 1704.00447 [cs.CV] (2017).
  4. Yang, Y., Sun, J., Li, H. & Xu, Z. ADMM-Net: A Deep Learning Approach for Compressive Sensing MRI. NIPS 10–18 (2017).
  5. Diamond, S., Sitzmann, V., Heide, F. & Wetzstein, G. Unrolled Optimization with Deep Priors. arXiv: 1705.08041 [cs.CV] (2017).
  6. Jin, K. H., McCann, M. T., Froustey, E. & Unser, M. Deep Convolutional Neural Network for Inverse Problems in Imaging. arXiv: 1611.03679 [cs.CV] (2016).
  7. Zhang, T. et al. Fast pediatric 3D free-breathing abdominal dynamic contrast enhanced MRI with high spatiotemporal resolution. J. Magn. Reson. Imaging 41, 460–473 (2015).
  8. Zhang, T., Pauly, J. M., Vasanawala, S. S. & Lustig, M. Coil compression for accelerated imaging with Cartesian sampling. Magn. Reson. Med. 69, 571–582 (2013).
  9. Johnson, K. M., Block, W. F., Reeder, S. B. & Samsonov, A. Improved least squares MR image reconstruction using estimates of k-space data consistency. Magn. Reson. Med. 67, 1600–1608 (2012).
  10. Cheng, J. Y. et al. Free-breathing pediatric MRI with nonrigid motion correction and acceleration. J. Magn. Reson. Imaging 42, 407–420 (2015).
  11. Moriguchi, H. & Duerk, J. Bunched phase encoding (BPE): a new fast data acquisition method in MRI. Magn. Reson. Med. 55, 633–648 (2006).
  12. Bilgic, B. et al. Wave-CAIPI for highly accelerated 3D imaging. Magn. Reson. Med. 73, 2152–2162 (2015).
  13. Chen, F. et al. Self-Calibrating Wave-Encoded Variable-Density Single-Shot Fast Spin Echo Imaging. J. Magn. Reson. Imaging (2017). doi:10.1002/jmri.25853
  14. Abadi, M. et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Distributed Systems. arXiv:1603.04467 [cs.DC] (2016).
  15. Uecker, M. et al. BART: version 0.3.01. (2016). doi:10.5281/zenodo.50726
  16. Wang, Z., Bovik, A. C., Sheikh, H. R. & Simoncelli, E. P. Image quality assessment: from error visibility to structural similarity. IEEE Trans Image Process. 13, 600–612 (2004).

Figures

Figure 1. Method overview. We start with subsampled multi-channel measurement data in the k-space domain. Sensitivity maps are estimated using ESPIRiT2 and applied with the adjoint of the imaging model AH. Subsampled k-space patch is inserted into a convolution neural network G to produce a fully sampled k-space patch. This patch is then inserted into the final k-space output. Two example patches are shown in blue and green with the corresponding images overlaid. By applying this network for all k-space patches, the full k-space data is reconstructed (upper right). The final image is shown in the lower right.

Figure 2. ISTA-based network architecture with two repeated blocks. For the m-th step with step-size tm, image yim is updated to yim+1 for the i-th k-space patch. Model B and its adjoint BH consist of the imaging model A (Fourier transform, sensitivity-map encoding) along with a window function W to avoid Gibbs ringing, subsampling, and phase from bandpass filtering. In the de-noising block, supplementary data dim, consisting of a low-resolution image and k-space patch location, are included by concatenation. Each convolutional layer is followed by batch normalization and rectified linear unit except for the final block (dotted green box).

Figure 3. Representative output from randomly selected bandpass-filtered input for uniform (a–c) and variable-density (d–f) poisson-disc subsampling. Input k-space data were padded (noted by the black bands in k-space) to the same 64x64 input size, and the data was passed through a ConvNet consisting of 8 “iteration” blocks. With nonlinear functions, the intermediary stages of the ConvNet does not always generate interpretable images. The final output with a final hard data projection stage has comparable results to the ground truth (last two columns).

Figure 4. Representative results. Test data (upper right) were subsampled with uniform (a, b) and variable-density (c, d) sampling masks (lower right) to generate the input data (left column). Images were reconstructed with a ConvNet trained on the entire image (second column) and with the proposed ConvNet with bandpass filtering (third column). Compressed-sensing-based parallel imaging reconstructions using L1-ESPIRiT are also displayed (fourth column). Without the need for hand tuning, the full ConvNet performed the best in terms of PSNR (highest), NRMSE (lowest), and SSIM (highest). The proposed bandpass network generated comparable results with little to no loss in quality.

Figure 5. Representative reconstruction of T2-weighted single-shot fast-spin-echo 2D scans with wave encoding. The proposed technique was adapted to support wave-encoding (subsampling in the bottom right). Compressed-sensing-based parallel imaging reconstruction (PI&CS) results are shown in the upper right and used as the training truth since no fully-sampled datasets were acquired. For testing, images were reconstructed with the proposed technique and PI&CS. Input (left) and bandpass ConvNet output (middle) are displayed along with the difference with the PI&CS. Residual aliasing artifacts remain (a) due to data inconsistencies possibly from motion. Image sharpness was recovered in both the proposed technique and PI&CS.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
3369