3330
Rapid Motion Compensation Reconstruction for Dynamic MRI using Pixel Tracking Temporal Total Variation Constraint1UCAIR, University of Utah, Salt Lake City, UT, United States, 2Physics and Astronomy, University of Utah, Salt Lake City, UT, United States, 3Cardiology, University of Utah, Salt Lake City, UT, United States
Synopsis
We present a novel motion compensation reconstruction method based on spatiotemporal constrained reconstruction (STCR) by tracking the movements of every pixel in each time frame, and constrain the temporal total variation along the pixel tracks. The proposed method can handle both respiratory and cardiac motion, and has comparable reconstruction speed but offers better image quality compared with STCR.
Introduction
In cardiac perfusion MRI, compressive sensing technique is being popularly used to acquire multiple slices within a short acquisition window. Temporal constraints in image domain have been well studied and demonstrated to be useful1,2. However, when motion is present the sparsity/smoothness assumptions could be invalid or temporal correlations could be difficult to exploit. Even though breath holding and ECG gating can assist to compensate motion, these methods can fail when patients cannot hold their breath sufficiently long or when the ECG signal is poor. Several attempts have been made to compensate motion during reconstruction. Reordering pixels in image domain to make the time curves monotonic3 or reordering frames to group similar motion states together4 have been used previously. Other approaches include estimating and applying deformation maps during iterations5-7 and using patch-based regularizations8,9. These approaches are typically computationally intensive, or break the time continuity of data. Here we propose a fast motion-compensation method based on the spatiotemporal constrained reconstruction (STCR), which calculates temporal total variation along the time track of each pixel, that provides rapid compressive sensing reconstruction for dynamic cardiac perfusion MRI when respiratory and cardiac motions are present.Theory and Method
In STCR, undersampled dynamic k-space data is reconstructed by exploiting the sparsity with spatial and temporal total variation constraints. Temporal total variation assumes pixel intensities in the object are temporally varying smoothly or in a piecewise smooth fashion. However, when inter-frame motion is present, this assumption breaks down since motion misaligns pixels representing the same feature along the time direction. To mitigate this problem, we propose to calculate the temporal total variation along the motion track of each pixel and term this pixel tracking temporal total variation (PTTTV). The cost function can be written as
$$ \left\|Am-d\right\|^2_2 + \lambda_t \left\|\sqrt{\nabla_tPm^2 + \epsilon}\right\|_1 + \lambda_s \left\|\sqrt{\nabla_xm^2 + \nabla_ym^2 + \epsilon}\right\|_1,$$
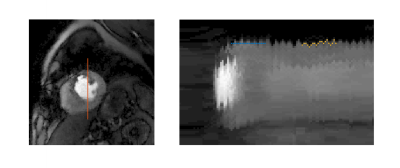
where $$$A$$$ is sampling matrix, $$$m$$$ is image to be reconstructed, $$$d$$$ is acquired data, $$$\lambda_{t,s}$$$ are constraint parameters, $$$\nabla_{t,x,y}$$$ are temporal and spatial gradient operators, $$$\epsilon$$$ is a small term to avoid singularity and $$$P$$$ is a reordering matrix produced from motion information that spatially aligns each pixel along time direction. The 1D case of pixel tracking total variation is shown in Figure 1.
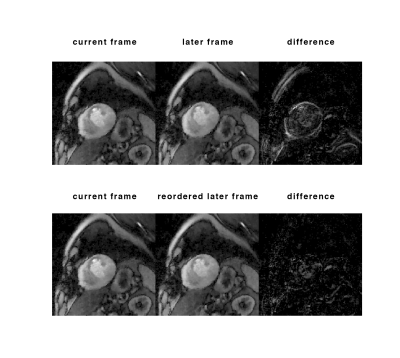
To acquire motion information, an artifact reduced reference image was first reconstructed by using STCR with $$$\lambda_t = 0.1C$$$, $$$\lambda_s = 0.03C$$$ and 20 conjugate iterations, where $$$C$$$ is the average intensity of the initial estimation, then denoised using a Gaussian low pass filter. Motion maps were estimated from this reference using large deformation kinematics with a greedy algorithm10. Similar to the MASTeR approach7, two sets of motion maps were estimated: forward motion maps that map each time frame to its later time frame and backward motion maps. We then detected the tracks of every pixel in the current frame, by finding its nearest moving position in adjacent frames from the motion maps. Pixels along the track were aligned using $$$P$$$. Figure 2 shows the pixel reordering and the improvement in temporal sparsity when aligning pixels along their tracks. Further reconstruction iterations when $$$P$$$ is applied used constraint parameters $$$\lambda_t = 0.3C$$$ and $$$\lambda_s = 0.03C$$$.
One gated and one ungated golden angle radial SMS datasets were used to test the PTTTV. Both datasets were acquired under regadenoson stress without breath holding using a turboFLASH sequence on a 3T Prisma (Siemens) scanner with TR/TE = 2.7/1.6ms, FOV = 260mm, voxel size 1.8mmx1.8mmx8mm. The reconstructions using PTTTV were compared with reconstructions using STCR.
Result and Discussion
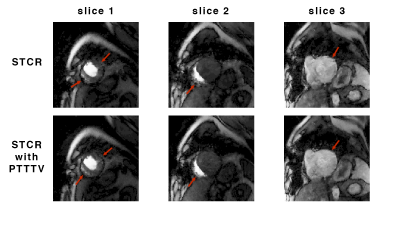
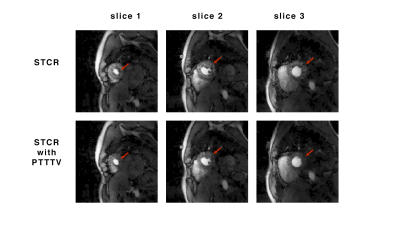
Figure 3 shows improvements in the gated dataset when using PTTTV in all simultaneously acquired slices. Figure 4 compares reconstructions with and without PTTTV for the ungated dataset. The proposed method can resolve both respiration and cardiac motion and improve image quality. The reconstruction is very fast since the greedy algorithm costs ~0.1s to estimate motion for each time frame of size 144x144 on an Intel Xeon E5 2.6GHz processor. The pre-calculated reference image can be used as initial estimation in later reconstruction iterations when incorporating $$$P$$$ to further reduce reconstruction time. While the proposed method could also be applied to other dynamic studies, comparing it with existing methods are warranted.Acknowledgements
References
[1] G. Adluru, C. McGann, P. Speier, E. G. Kholmovski, A. Shaaban, E. V.R. DiBella. Acquisition and reconstruction of undersampled radial data for myocardial perfusion MRI. J Magn Reson Imaging, 2009 Feb; 29(2): 466–473.
[2] L. Feng, MB. Srichai, RP. Lim, A. Harrison, W. King, G. Adluru, EV. DiBella, DK. Sodickson, R. Otazo, D. Kim. Highly Accelerated Real-Time Cardiac Cine MRI Using k–t SPARSE-SENSE. MRM. 2013; 70:64-74.
[3] G. Adluru, EVR. DiBella. Reordering for Improved Constrained Reconstruction from Undersampled k-Space Data. International Journal of Biomedical Imaging. 2008; 341684.
[4] L. Feng, S. Coppo, D. Piccini, J. Yerly, PG. Masci, M. Stuber, DK. Sodickson, R. Otazo. 5D Whole-Heart Sparse MRI. MRM 2017; 75(2):775-88.
[5] G. Adluru, E. DiBella. Reconstruction with Diffeomorphic Motion Compensation for Undersampled Dynamic MRI. SPIE 2013.
[6] S. Lingala, E. DiBella, M. Jacob. Deformation Corrected Compressed Sensing (DC-CS): A Novel Framework for Accelerated Dynamic MRI. 2015; 34 1.
[7] M. S. Asif, L. Hamilton, M. Brummer, J. Romberg. Motion-Adaptive Spatio-Temporal Regularization for Accelerated Dynamic MRI, Magnetic Resonance in Medicine, 2013; 70:800–812.
[8] Y. Q. Mohsin, S. J. Lingala, E. DiBella, M, Jacob, Accelerated Dynamic MRI Using Patch Regularization for Implicit Motion Compensation, MRM, 2017; 77:1238-1248.
[9] H. Jung, S. Kyunghyun, S.N. Krishna, K.Y. Eung, Y.C. Jong. k-t FOCUSS: A General Compressed Sensing Framework for High Resolution Dynamic MRI. MRM 2009; 61:103-116.
[10] G. E. Christensen, R. D. Rabbitt, M. I. Miller. Deformable Templates Using Large Deformation Kinematics. IEEE Transactions On Image Processing. 1996; 5(10).
Figures