3235
Investigating Diffusion-MRI based neurite density estimation model dependency: an in-vivo study on the HCP dataset1University Of Verona, Verona, Italy, 2Université De Sherbrooke, Sherbrooke, QC, Canada
Synopsis
Diffusion MRI can be used to estimate the brain tissue neurite density from Multi-Compartment models. This index corresponds to the “stick” compartment volume fraction estimated in every voxel. In this work, we provide evidence that the distribution of stick volume fraction is characteristic of the brain tissue and is highly reproducible between subjects but strongly depends on the underlying multi-compartment model definition. In particular, in-vivo results on 10 subjects of the Human Connectome Project show that the neurite density distribution depends on both the stick parallel diffusivity and the extra-axonal compartment model.
INTRODUCTION
Neurite density1,2,3,4,5 is one of the most promising microstructural features that can be estimated from Diffusion Magnetic Resonance Imaging (Diffusion-MRI) multi-shell data. This index, also called intra-axonal volume fraction (νia) is calculated from Diffusion-MRI Multi-Compartment models as the “stick” compartment volume fraction6. Recent years have seen a proliferation of Multi-Compartment models developed to estimate the brain tissue microstructure from the diffusion signal7. Each of these models makes different assumptions about the values of the diffusivity coefficient and the number of compartments. Even subtle changes in the models have a deep impact on the resulting neurite density estimation. In this work, we aim at investigating the potential of the stick volume fraction considering: i) its inter-subject reproducibility, and ii) the effect of the other model parameters on its estimation in-vivo.METHODS
In this work, we analyzed ten subjects of the WU-MINN Human Connectome Project8 (HCP) project using three multi-compartment models: Neurite Orientation Dispersion and Density Imaging2 (NODDI), Ball & Stick6 (BS), and Multi-Compartment Microscopic Diffusion Imaging9 (MC-MDI). All these models represent the intra-axonal compartment as a stick and present only two parameters to be fitted. NODDI and BS fix the parallel diffusivity at 1.7x10-3mm2/s, while in MC-MDI it is a free parameter. BS extra-axonal compartment is modeled using an isotropic Gaussian, while NODDI and MC-MDI use an axially symmetric Gaussian which perpendicular diffusivity depends on the extra-axonal volume fraction and the parallel diffusivity following a tortuosity model2,9. NODDI model contains also a third compartment representing the cerebrospinal fluid. In this work, we use the Spherical Mean Technique7,9,10 version of NODDI and BS, respectively NODDI-SH6,10 and BS-SH6, for estimating the model parameters in a unified framework.RESULTS
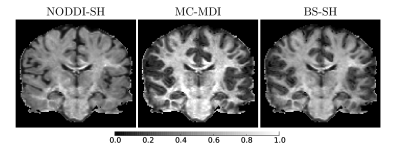
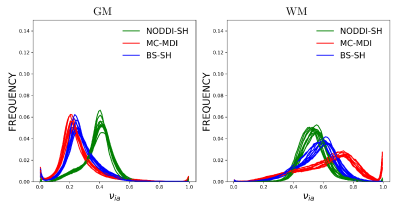
Figure 1 shows νia maps calculated for the considered models for one HCP subject. The neurite density is higher, as expected, in the White Matter (WM) with respect to the Gray Matter (GM), for all the models. The corpus callosum and the corticospinal tract show the highest νia in particular near the brainstem. MC-MDI neurite density index presents the highest values in comparison with NODDI-SH and BS-SH, confirming the previous results obtained on simulated data7. NODDI-SH exhibits the lowest contrast between GM and WM, compared to MC-MDI and BS-SH. Figure 2 shows the histograms of νia for WM and GM for all the models in ten HCP subjects. The estimated neurite density is stable across subjects in both GM and WM for all the models. BS-SH and MC-MDI present similar distribution of values for GM, while NODDI-SH νia values are closer to the ones obtained in WM. In WM, MC-MDI presents the highest values of νia followed by BS-SH and NODDI-SH.DISCUSSION
MC-MDI is the only model among those considered that leaves the stick parallel diffusivity as a free parameter. This approach leads to the highest WM-GM contrast with respect the other models. MC-MDI neurite density reaches values close to one in brain areas presenting a single fiber bundle. Although such areas present a higher packaging of axons it is unlikely for the extra-axonal signal to disappear completely, therefore, this estimation is probably influenced by the noise or the unsuitability of the model itself. As previously reported3,4,5, considering a fixed parallel diffusivity value everywhere in the brain is biologically implausible. However, this fact does not explain the difference between BS-SH and NODDI-SH. Both models consider the same stick diffusivity and provide different νia maps, in particular in GM. NODDI cerebrospinal fluid compartment volume fraction is zero in all the GM, therefore, the only difference between these models is their extracellular space representation. Such change between the two models is enough to modify the neurite density profile in all the GM.CONCLUSION
Neurite density shows some potentials for its possible application in clinical studies: it has a well defined numerical range and it is stable across healthy subjects. However, its values strongly depend on the choice of the model used to calculate it. These results hinder the underlying assumption that the stick volume fraction actually corresponds to the histological neurite density, although a correlation between these two features has been previously shown1. Our results suggest that the stick volume fraction could potentially be used as a feature to discriminate between healthy brains and pathological conditions. However, it is extremely important to keep in mind that its values do not represent the real underlying neural density, especially in pathological conditions, and to compare it only with studies that use exactly the same model for its estimation.Acknowledgements
Data were provided by the Human Connectome Project, WU-Minn Consortium(Principal Investigators: David Van Essen and Kamil Ugurbil; 1U54MH091657)funded by the 16 NIH Institutes and Centers that support the NIH Blueprint forNeuroscience Research; and by the McDonnell Center for Systems Neuroscienceat Washington University.References
1. Jespersen, S.N., Bjarkam, C.R., Nyengaard, J.R., Chakravarty, M.M., Hansen, B.,Vosegaard, T., Stergaard, L., Yablonskiy, D., Nielsen, N.C., Vestergaard-Poulsen,P. (2010) : Neurite density from magnetic resonance diffusion measurements at ultrahighfield: Comparison with light microscopy and electron microscopy. NeuroImage49(1) 205 – 216
2. Zhang, H., Schneider, T., Wheeler-Kingshott, C. A., and Alexander, D. C. (2012). NODDI: practical in vivo neurite orientation dispersion and density imaging of the human brain. Neuroimage, 61(4), 1000-1016.
3. Lampinen, B., Szczepankiewicz, F., Mårtensson, J., van Westen, D., Sundgren, P. C., & Nilsson, M. (2017). Neurite density imaging versus imaging of microscopic anisotropy in diffusion MRI: A model comparison using spherical tensor encoding. NeuroImage, 147, 517-531.
4. Novikov, D. S., Jespersen, S. N., Kiselev, V. G., and Fieremans, E. (2016). Quantifying brain microstructure with diffusion MRI: Theory and parameter estimation. arXiv preprint arXiv:1612.02059.
5. Reisert, M., Kellner, E., Dhital, B., Hennig, J., & Kiselev, V. G. (2017). Disentangling micro from mesostructure by diffusion MRI: A Bayesian approach. NeuroImage, 147, 964-975.
6. Behrens, T. E., Woolrich, M. W., Jenkinson, M., Johansen Berg, H., Nunes, R. G., Clare, S., and Smith, S. M. (2003). Characterization and propagation of uncertainty in diffusion weighted MR imaging. Magnetic resonance in medicine, 50(5), 1077-1088.
7. Zucchelli, M., Descoteaux, M., Menegaz, G. (2017), A generalized SMT-based framework for Diffusion MRI microstructural model estimation. Proceedings of "Medical Image Computing and Computer Assisted Intervention (MICCAI), Workshop on Computational Diffusion MRI (CDMRI)" , Quebec City, Canada.
8. Sotiropoulos, S.N., Jbabdi, S., Xu, J., Andersson, J.L., Moeller, S., Auerbach,E.J., Glasser, M.F., Hernandez, M., Sapiro, G., Jenkinson, M., et al. (2013): Advancesin diffusion MRI acquisition and processing in the human connectome project.NeuroImage 80 125–143
9. Kaden, E., Kelm, N. D., Carson, R. P., Does, M. D., and Alexander, D. C. (2016). Multi-compartment microscopic diffusion imaging. NeuroImage, 139, 346-359.
10. Zucchelli, M., Descoteaux, M., & Menegaz, G. (2017). NODDI-SH: a computational efficient NODDI extension for fODF estimation in diffusion MRI. arXiv preprint arXiv:1708.08999.
Figures