3194
Correcting a slice distortion artifact in the multiband diffusion images by postprocessing with the known diffusion gradients1University of Southern California, Los Angeles, CA, United States
Synopsis
The diffusion weighted images acquired with the multiband sequence or the Lifespan protocols shows a type of slice distortion artifact. This artifact is caused by the eddy currents, which can be induced by the diffusion gradient associated with either the current DW image or the previous DW images. The artifact can be corrected by a correction algorithm which includes the diffusion gradients from both the current and previous DW images.
Introduction
Diffusion weighted imaging (DWI) has become a popular tool to provide information about the intrinsic architecture of white matter in the human brain. The recently developed multiband (MB) slice-accelerated technique can provide high angular resolution for measuring the diffusion signals in shorter time length than conventional EPI sequence [1], especially in Human Connectome Lifespan projects. However the diffusion weighted images acquired with the multiband sequence or the Lifespan protocols shows a type of slice distortion artifact. We found that this artifact is caused by the eddy currents, induced by the diffusion gradient associated with either the current or the previous DW images. How to correct this artifact post hoc should be investigated and will be addressed here.Materials and Methods
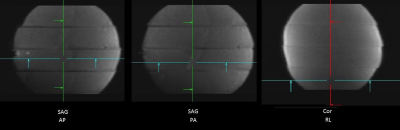
DWI data were acquired using multiband sequence with the following parameters as in the Lifespan projects: TR = 3222 msec, TE = 89.2 msec, 197 diffusion gradient directions, 92 axial slices for whole brain coverage, MB factor as 4, and maximum b value as 2000 s/mm^2. One fBIRN phantom and two adults were scanned on a Siemens 3T Trio Prisma MRI system. To study the nature of this artifact, we changed the slice order from interleaved into ascending, and switch the phase encoding direction into AP, PA and RL in the DWI scans on the fBIRN phantom.
To correct the diffusion weighted images which already have this artifact, we apply an algorithm for correcting the eddy current distortions using the known diffusion gradients [2]. With the current diffusion gradient Gi and the previous one Gi-1 considered, the resulting distortion in translation Dti from the alignment between the images of the i-th diffusion gradient and the 1st gradient can be calculated for i > 1 as Equation 1
$$D_{ti}=G_{i}\cdot T+\alpha G_{i-1}\cdot T-G_{1}\cdot T$$
where the vector T are the translations along the phase encoding direction induced by the corresponding unit changes in the x, y, and z gradients, and α is the decay factor of eddy current from Gi-1 at the time point of i-th DW image.
Therefore, the three unknown elements of vector T can be calculated as Equation 2
$$T=(G'^{T}\cdot G')^{-1}\cdot G'^{T}\cdot D_{t}$$
where the rows of matrix G' are formed by $$$(G_{ix}+\alpha G_{i-1x}-G_{1x}, G_{iy}+\alpha G_{i-1y}-G_{1y}, G_{iz}+\alpha G_{i-1z}-G_{1z})$$$ for the i-th diffusion gradient.
Similarly, vectors S for the shear distortion and M for the the scaling (or magnification) distortion induced by a unit change of the x, y, and z components of the gradient can be calculated using Equations 3 and 4
$$S=(G'^{T}\cdot G')^{-1}\cdot G'^{T}\cdot D_{s} $$
$$M=(G''^{T}\cdot G'')^{-1}\cdot G''^{T}\cdot D'_{m}$$
where the G'' is formed as $$$(G_{ix}+\alpha G_{i-1x}-D_{mi}G_{1x}, G_{iy}+\alpha G_{i-1y}-D_{mi}G_{1y}, G_{iz}+\alpha G_{i-1z}-D_{mi}G_{1z}) $$$and $$$D'_{mi} = D_{mi} –1$$$ for i>1.
Given the model parameters for the distortions T, S, and M, the image distortions can be corrected by reverse application of these parameters to the distorted DW images.
Results
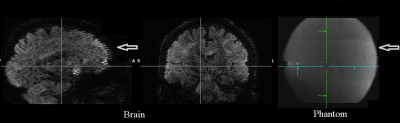
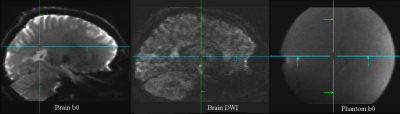
In the original image (Figure 1), an artifact shows up as misalignment between slices in both the diffusion weighted images and b0 images in both human and phantom data. The results from ascending and descending order and the PA and AP phase encodings show that they reverse the slice stretch and shrink at the sagittal view, and RL phase encoding makes the slice shift at the coronal view (Figure 2). It is a typical eddy current effect but presented on the multiband images. This artifact also seen on the b0 images, indicates that the super short TR and super high diffusion gradient strength in the MB protocols make it possible that the eddy current affects different images across TR. Thus the proper eddy current correction algorithm should include not only the current diffusion gradient but also the previous diffusion gradient. After corrected by this way, i.e. the Equations 2-4, the artifact is reduced to the minimal level (Figure 3).Conclusion
The slice distortions shown in the diffusion weighted images acquired with the multiband sequence or the Lifespan protocols is caused by the eddy currents, which can be induced by the diffusion gradient associated with either the current DW image or the previous DW images. It can be corrected by a correction algorithm which includes the known diffusion gradients from both the current and the previous DW images.Acknowledgements
No acknowledgement found.References
[1] Feinberg, et al., PloS ONE: e15710, 2010.
[2] Zhuang, et al., JMRI: 1460, 2013.