Purpose

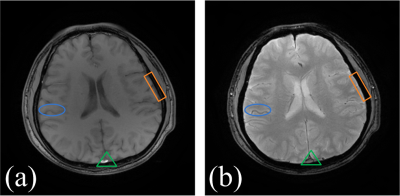
In magnetic resonance imaging (MRI), low-resolution images may be acquired and their resolutions can be improved by applying super-resolution methods. MRI usually offer images of an object with different contrasts, e.g. T1-weighted or T2-weighted imaging (Fig. 1). Thus the shared information between inter-contrast images can be used to benefit super-resolution [1]. In this paper, we first establish a gradient relation model among different contrast images and then reconstruct the super-resolved edges by incorporating the gradient information from another contrast high-resolution image. Brain image edges are further improved with similar patches estimation and iterative back-projection filter. The reconstructed edges are more consistent to the original high-resolution image, indicated with higher peak signal-to-noise ratio (PSNR) and structure similarity index (SSIM) [2] than the compared methods.

Methods

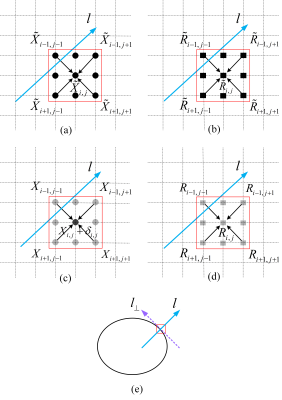
Multi-contrast images $$${\bf{\tilde X}}$$$ and $$${\bf{\tilde R}}$$$ are assumed to possess the same gradient direction in a local pattern. We proposed to establish a relation model of gradient value between different contrast images (Fig. 2), to restore a high-resolution image from its input low-resolution version. Assuming that an adjustment parameter $$${\delta _{i,j}}$$$ is added to the (i, j) pixel $$${X_{i,j}}$$$ of a pre-interpolated image $$${\bf{X}}$$$ , our model can be expressed as $$\begin{array}{l} \mathop {\min }\limits_{{\delta _{i,j}}} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\{ {\kern 1pt} [g({X_{i,j}} + {\delta _{i,j}}) - g({X_{i,j}})] - \lambda {\kern 1pt} {\kern 1pt} [g({{\tilde R}_{i,j}}) - g({R_{i,j}})]\} ^2}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} + {\{ [{g_ \bot }({X_{i,j}} + {\delta _{i,j}}) - {g_ \bot }({X_{i,j}})] - {\lambda _ \bot }{\kern 1pt} {\kern 1pt} [{g_ \bot }({{\tilde R}_{i,j}}) - {g_ \bot }({R_{i,j}})]\} ^2} \end{array} (1)$$ where $$$g\left( \cdot \right)$$$ is a second order gradient function, $$${\tilde X_{i,j}}$$$ is the pixel of $$${\bf{\tilde X}}$$$, and $$${\tilde R_{i,j}}$$$ is the pixel of $$${\bf{\tilde R}}$$$. $$${R_{i,j}}$$$ is the pixel of $$${\bf{R}}$$$, which is the pre-interpolated image of LR version of $$${\bf{\tilde R}}$$$. The $$$\lambda $$$ and $$${\lambda _ \bot }$$$ are parameters that adjusting intensity in gradient direction and the edge direction. In here, their values are estimated as SRGR model [3] as $$\begin{array}{l} \lambda = ({X_{i + 1,j - 1}} - {X_{i - 1,j + 1}})/{\kern 1pt} {\kern 1pt} {\kern 1pt} ({{\tilde R}_{i + 1,j - 1}} - {{\tilde R}_{i - 1,j + 1}}){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \\ {\lambda _ \bot } = ({X_{i - 1,j - 1}} - {X_{i + 1,j + 1}})/{\kern 1pt} {\kern 1pt} {\kern 1pt} ({{\tilde R}_{i - 1,j - 1}} - {{\tilde R}_{i + 1,j + 1}}){\kern 1pt} .{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \end{array} (2)$$ The proposed model finds refinements on pixels to minimize the gradient difference between the HR images and HR reference images. The similarity of image patches [1, 4-5] is employed to estimate intensity parameters, leading a more accurate reconstructed image. Then, iterative back-projection (IBP) filter [6] is applied to the reconstructed image to further increase image quality.

Results

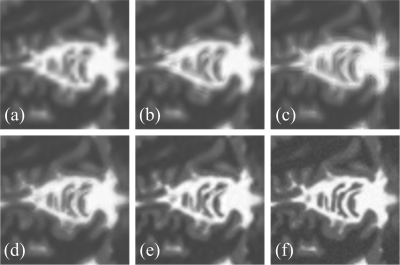
Experimental results on synthetic MRI images are presented in Fig. 3. The new approach, whether without IBP or with IBP, achieves higher visual quality and higher objective quality criteria (PSNR and SSIM [2]) than the compared state-of-the-art super-resolution approaches.

Conclusions

The gradient information of the multi-contrast MRI images is very useful. With a proper relation model, the proposed method enhances image edges in MRI image super-resolution.

Acknowledgements

This work was supported by the National Key R&D Program of China (2017YFC0108700), National Natural Science Foundation of China (61571380, U1632274 and 61302174), Natural Science Foundation of Fujian Province of China (2016J05205). The correspondence should be sent to Dr. Xiaobo Qu (Email: quxiaobo@xmu.edu.cn).