Introduction

Alzheimer’s disease (AD) is the most common dementia and its prevalence is expected to increase as the population continues to age.1 Biomarkers are important tools to better understand disease mechanisms, aid in early diagnosis, and provide objective measures of therapeutic efficacy. Previous studies have shown that global brain stiffness is reduced due to AD,2 and that stiffness changes follow the expected regional pattern on a coarse, lobar scale.3 In these previously employed methodologies, stiffness estimates were heavily weighted by white matter. Given that pathology is particularly prevalent in cortical gray matter, the purpose of this work was to investigate if stiffness estimates more heavily weighted by cortical gray matter would be more sensitive to AD pathophysiology. We employed a recently developed neural network-based inversion (NNI) with improved performance in smaller, cortical-centric regions of interest (ROIs) for this study.4

Methods

First, the NNI was trained on 1 million simulated training examples with an additional 200,000 examples used for validation. These 3D displacement fields were each assigned a randomly chosen stiffness between 0.1 and 5 kPa with waves propagating radially from up to 10 point sources (placed randomly outside the simulated patch), and with SNR chosen randomly between 1 and 20. The features provided to the artificial neural network included the real and imaginary parts of the first temporal harmonic of the displacement data in a 3x3x3 neighborhood. The network was trained with scaled conjugate gradient backpropagation,5 stopping when error was not reduced for 6 consecutive iterations in the validation set. Data for this study were taken from previously completed studies on repeatability6 and AD,3 where details on data acquisition can be found. For each subject, a brain mask was computed using SPM-computed segmentations, where the mask included voxels in which the proportion of gray plus white matter was greater than cerebrospinal fluid. Thirty-one regions of interest were defined using a modified Automated Anatomical Labeling (AAL) atlas,7 and were put into subject-space by applying the inverse deformation computed during normalization. To compute gray matter stiffness in each ROI, the displacement data were first masked by the intersection of the brain mask and atlas region. The curl of the displacement field was then computed and smoothed using previously described edge-aware methods.6 To avoid evaluating the NNI with missing data, the smoothed curl images were then “dilated” by creating a composite image equal to a smoothed curl image outside the ROI and equal to the originally computed curl inside the ROI. Stiffness maps were computed by evaluating the trained NNI at each voxel in the ROI, and mean stiffness was calculated from voxels where the proportion of gray matter was greater than that of white matter plus cerebrospinal fluid. Test-retest reliability was assessed in 10 volunteers who were each scanned 3 times. The coefficient of variation (CV) was calculated for each ROI. Stiffness was then computed in 32 cognitively normal (CN) subjects (16 amyloid-negative and 16 amyloid-positive) as well as 8 amyloid-positive subjects with probable AD. The area under the receiver operating characteristic curve (AUROC) was computed for each ROI, and compared to previously published methods.

Results

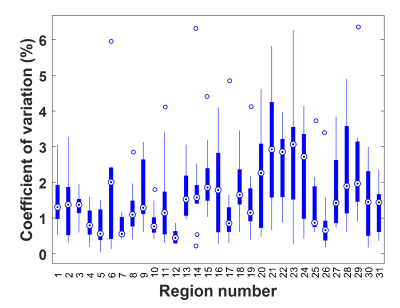
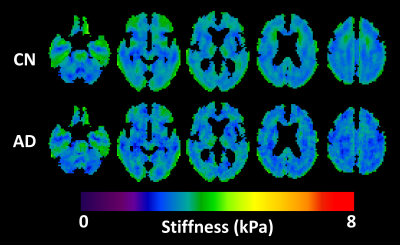
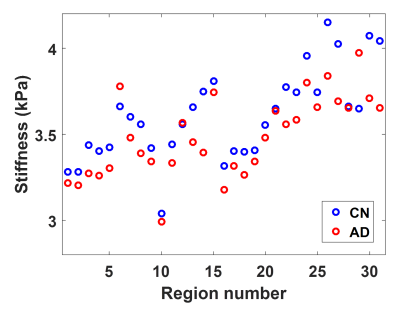
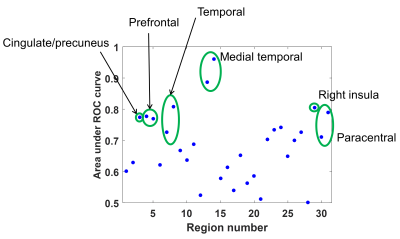
The summary of test-retest repeatability is shown in Figure 1. The median CV across all ROIs was 1.36%, comparable to previously described methods.6,8 Mean stiffness maps in the CN and AD groups are shown in Figure 2, along with a summary of the mean stiffness in each ROI in Figure 3. Stiffness estimates are in the expected range and not substantially underestimated as typically observed due to partial volume effects.6 Finally the AUROC for differentiating CN and AD subjects for each ROI is summarized in Figure 4. Of note, the medial temporal lobe has the greatest discriminatory power (AUROC=0.96 when left and right are averaged). This AUROC is higher than the composite frontal/parietal/temporal lobe ROI previously reported (AUROC=0.87),3 despite the substantially reduced ROI size.

Discussion

While white matter still contributes to these results, these stiffness estimates are more heavily weighted toward cortical gray matter based on ROI selection. The NNI provided reliable stiffness measurements even in these small ROIs. Interestingly the medial temporal lobe, which is known to be strongly impacted by AD, was the most sensitive region to AD pathophysiology. This decrease in stiffness was detectable despite the apparent overestimate of the stiffness at the brain’s edge with NNI, based both on simulation experiments (not shown) and visual inspection of the stiffness maps (Fig. 2). With improved treatment of the brain’s edge, stiffness may be even more sensitive to AD pathology than these results indicate.

Acknowledgements

This work was supported by the National Institutes of Health grant R37-EB001981.