3119
Prostate Cancer Classification Using Stretched Exponential Model Parameters of Diffusion Signal Decay1Richard and Loan Hill Department of Bioengineering, University of Illinois at Chicago, Chicago, IL, United States, 2Urology, University of Illinois at Chicago, Chicago, IL, United States, 3Center for Magnetic Resonance Research, College of Medicine, University of Illinois at Chicago, Chicago, IL, United States, 4Radiology, University of Illinois at Chicago, Chicago, IL, United States, 5Pathology, University of Illinois at Chicago, Cahicago, IL, United States, 6Neurosurgery, University of Illinois at Chicago, Chicago, IL, United States, 7Richard and Loan Hill Department of Bioengineering, University of Illinois, Chicago, IL, United States
Synopsis
Prostate cancer is a common malignancy among men. Using MRI to discriminating high-grade disease from benign and indolent cancer in the prostate is highly desirable for treatment planning. Single and multi- exponential models of diffusion signal decay in the prostate has proven useful for determining prostate cancer tissue structure. However, classification of cancer grade remains illusive. In this study, we investigate the stretched exponential signal decay model using histology and ROC analysis to determine if it will more accurately characterize aggressive prostate cancer.
Introduction
Prostate cancer is one of
the most common malignancy among men in the US [9]. Diffusion-weighted MRI
(DWI) plays an important role in providing important biological information on
regional changes in prostate tissue. The
most commonly used method for DWI is a single exponential signal decay to
generate a spatial map of the apparent diffusion coefficient (ADC, mm2/s).
DWI studies of the prostate showed the usefulness of single exponential signal
decay on noninvasively determining human tissue structure [4],[8],[10]. However,
diffusion weighted signal decay in the prostate does not follow a single
exponential pattern and therefore, it is inadequate to differentiate between
benign prostate inflammation and hyperplasia [3]. To overcome this problem,
Bennett et al. [1] introduced the stretched exponential model. It has been
shown that the stretched exponential signal decay model parameters provide more
information about tumor than ADC [5-7]. In this study, we show the ability of
using a stretched exponential model to establish the correspondence between the
DDC and α -maps with histological sections of
the entire prostate gland to characterize aggressiveness
of prostate cancer.
Methods
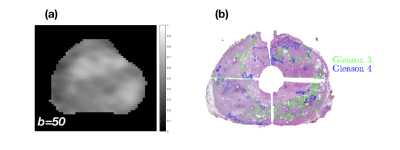
Patients. This study enrolled a total of 10 patients with high-grade proven prostate cancer. Imaging. (a) MR Protocol. Patients were scanned on a 3T multi-parametric MRI (GE Healthcare, Discovery 750 MRI), Figure 1a, prior to radical prostatectomy (RP). DWI images (TR 2500 ms, TE 68 ms, FOV 28x28 cm2, matrix 256x256, resolution 1.09 mm) were acquired at multiple b-values (50, 500, 1000, 1500, and 2000 s/mm2) with the corresponding averages (2, 4, 8, 12, and 16). The slice thickness was 3 mm for all sequences. (b) Histology Protocol. Whole embedded RP sections were digitized at 20X magnification using a digital scanner (Scanscope CS, Aperio Technologies), and all tumor foci were annotated (Aperio ImageScope 11.2.0.780, Leica Biosystems) by Gleason pattern (Figure 1b) by a board certified genitourinary pathologist. A zonal scheme was devised for matching the MRI to the RP sections based on the orientation to the urethra (anterior/posterior, left/right, level from base to apex). Model fitting. The multi-b-value diffusion data were fitted to the mono-exponential model. using the following equation: $$S = S_0 e^{(-b\times ADC)}.$$ To quantify the degree of tissue heterogeneity, the multi-b-value diffusion data were fitted to the stretched exponential model, [1] using the following equation: $$S = S_0 e^{[-(b \times DDC)^\alpha ]},$$ where DDC (mm2/s) is the distributed diffusion coefficient , and α (0 < α < 1) is a heterogeneity index that characterizes the multi-exponential nature of diffusion-related signal decay [2]. The data was fit pixel by pixel for selected slices to the mono-exponential and to the stretched-exponential models using a nonlinear least squares fitting algorithm in Matlab (MathWorks). Statistical Analysis. Fifty-two (52) target quadrant regions were identified as healthy or unhealthy from one patient. The performance of the stretched exponential model for differentiating between benign prostate inflammation and hyperplasia was evaluated and compared with the mono-exponential model using a receiver operating characteristic (ROC) analysis. ROIs were drawn by using the means of each quadrants of ADC, DDC, and α. Multivariate logistic regression was used to combine the stretched exponential model parameters (DDC, and α). All statistical analyses were carried out using Matlab (MathWorks).Results
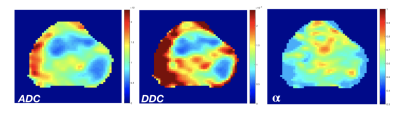
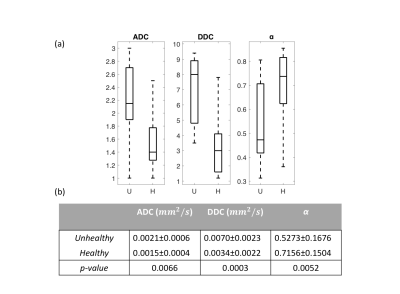
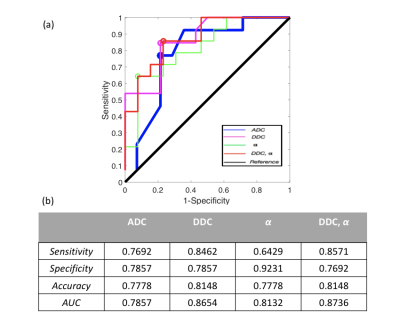
Figure 2 shows a whole prostate ADC, DDC, and α maps from a representative patient. Figure 3a shows the group analysis as presented in the boxplots of the mean ADC, DDC, and α. Figure 3b shows the corresponding descriptive statistics, exhibiting sample mean and standard deviation, (±σ), of ADC, DDC, and α for healthy and unhealthy. All parameters show significant differences (p-values<0.05) between healthy and unhealthy. Figure 4 shows the ROC results for the ADC, DDC, α, and combined (DDC,α) parameters. The ROC of combined (DDC,α) parameters yielded the highest sensitivity (0.857), and area under the curve (AUC = 0.874).Discussion and Conclusion
ADC maps are sensitive to regional changes in prostate tissue, however, their diagnostic specificity is not enough for distinguishing between benign prostate inflammation and hyperplasia [3]. The results showed that the stretched-exponential model with multi-b values diffusion data has potential in establishing the correspondence between the DDC and α -maps with histological sections of the entire prostate gland. The ROC analysis showed that the combination of the stretched exponential model parameters is more accurate of differentiating high grade prostate cancer from benign and indolent prostate cancer.Acknowledgements
This research was supported by Department of Defense PRTA W81XWH-15-1-0346 (Abern).References
[1] Kevin M Bennett et al. Characterization of continuously distributed cortical water diffusion rates with a stretched-exponential model. Magnetic resonance in medicine, 50(4):727–734, 2003.
[2] MN Berberan-Santos et al. Mathematical functions for the analysis of luminescence decays with underlying distributions 1. kohlrausch decay function (stretched exponential). Chemical Physics, 315(1):171–182, 2005.
[3] Jonathan I Epstein et al. Upgrading and downgrading of prostate cancer from biopsy to radical prostatectomy: incidence and predictive factors using the modified gleason grading system and factoring in tertiary grades. European urology, 61(5):1019–1024, 2012.
[4] Kazuhiro Kitajima, Yasushi Kaj et al. Prostate cancer detection with 3 t mri: Comparison of diffusion-weighted imaging and dynamic contrast-enhanced mri in combination with t2-weighted imaging. Journal of Magnetic Resonance Imaging, 31(3):625–631, 2010.
[5] Thomas C Kwee et al. Intravoxel water diffusion heterogeneity imaging of human high-grade gliomas. NMR in biomedicine, 23(2):179–187, 2010.
[6] Xiaohang Liu et al. Comparison of stretched-exponential and mo- noexponential model diffusion-weighted imaging in prostate cancer and normal tissues. Journal of Magnetic Resonance Imaging, 42(4):1078–1085, 2015.
[7] Yousef Mazaheri et al. Diffusion-weighted magnetic resonance imaging of the prostate: improved robustness with stretched exponential modeling. Journal of computer assisted tomography, 36(6):695–703, 2012.
[8] Rajakumar Nagarajan et al. Correlation of gleason scores with diffusion-weighted imaging findings of prostate cancer. Advances in urology, 2012, 2011.
[9] Lindsey A Torre et al. Jemal. Global cancer statistics, 2012. CA: a cancer journal for clinicians, 65(2):87–108, 2015.
[10] Bashar Zelhof et al. Correlation of diffusion-weighted magnetic resonance data with cellularity in prostate cancer. BJU international, 103(7):883–888, 2009.
Figures