3099

Biomimetic numerical phantoms for white matter tissues characterization using a reduced number of design parameters
Kevin GINSBURGER1, Fabrice POUPON2, Felix MATUSCHKE3, Jean-François MANGIN2, Markus AXER3, and Cyril POUPON1

1UNIRS, CEA/ISVFJ/Neurospin, Gif-sur-Yvette, France, 2UNATI, CEA/ISVFJ/Neurospin, Gif-sur-Yvette, France, 3INM-1 Forschungszentrum Jülich, Jülich, Germany

Synopsis

We propose to extend the functionalities of the Diffusion Microscopist Simulator to design more realistic white matter phantoms without any input mesh and with few parameters. The biomimetic phantoms can represent crossing configurations with an arbitrary number of fiber populations, include a myelin sheath and Ranvier nodes and account for beading, tortuosity and angular dispersion of fibers.

Introduction

Characterizing brain white matter (WM) ultrastructure at cellular scales is a major challenge of diffusion MRI (dMRI). Most current approaches use WM multicompartmental models either relying on analytical or simulation-based methods using oversimplistic geometries which might not catch the complexity of real biological tissues1,2,3. Monte-Carlo simulations of spins Brownian motion might overcome this issue by enabling dMRI signal synthesis from any diffusing medium geometries and allowing to model any further biophysical process occurring in tissues. State-of-the-art Monte-Carlo simulators only generate a limited number of geometries. For instance, Camino4 is limited to substrates with straight cylinders (including crossing fibers and global angular dispersion) or constructed from histological images which have to be segmented and lead to very computationally demanding simulations. We thus propose to extend the Diffusion Microscopist Simulator5 functionalities to design more realistic WM phantoms relying on a reduced set of design parameters. The biomimetic phantoms can represent crossing configurations with an arbitrary number of fiber populations, with more realistic fiber representations including a myelin sheath and Ranvier nodes and account for beading, tortuosity and angular dispersion.

Methods

The phantom generation algorithm takes a maximal number of $$$14N+2$$$ parameters to generate complex axonal geometries, where $$$N$$$ is the number of fiber populations. At each step, the absence of intersection between fibers is ensured.

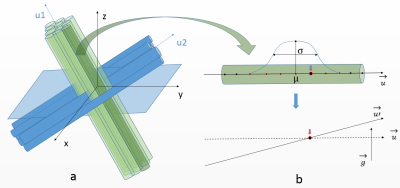
First, a set of oversimplistic fiber populations is constructed. Each population is defined by an orientation, a Gamma distribution of fiber envelopes radii and an intracellular fraction, amounting to 4 parameters (fig. 1). A population corresponds to rectilinear and parallel fibers outer envelopes, represented by control points with corresponding outer radii values. In the case of multiple populations, the degree of interweaving of fibers from different populations is ruled by 2 scale parameters controlling the distance between axons within the same population, thus enabling to create aggregated structures or sheet organizations6 where fibers find their way amongst other populations.

The second and third steps consist in inducing global orientation dispersion (fig. 1) and local tortuosity7 in the geometry (fig. 2.a), amounting to 2 parameters.

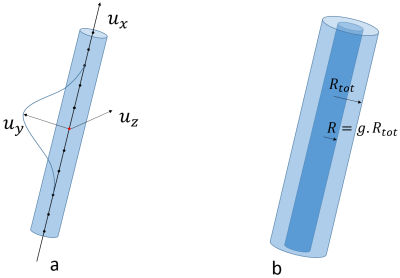
The axonal membrane is then created within the fiber envelope with a radius computed from a predefined $$$g$$$-ratio (ratio between the axonal membrane and the outer fiber diameters). For each population, the $$$g$$$-ratio follows a Gamma distribution (2 parameters). The myelin sheath corresponds to the space between the axonal membrane and the fiber outer envelope (fig. 2.b).

The algorithm also accounts for the presence of Ranvier nodes in the myelin sheath (fig. 3.a). The internode distance $$$d$$$ is set by the maximal conduction relationship8 $$$ d / D = k g \sqrt{( \log( 1/g ) )}$$$ where $$$k$$$ is some constant and $$$D$$$ is the external diameter of myelin. The size of each Ranvier node is computed as a ratio of the internodal length9, following a Gamma distribution (2 parameters).

Our algorithm also represents beading caused by cytoskeletal damage of the axon membrane: the contour of both axonal and myelin cylinders is swollen using adequate functions like sinusoidal lobes (fig. 3.b). The amplitude and spacing of those lobes both follow a Gamma distribution (4 parameters).


Results

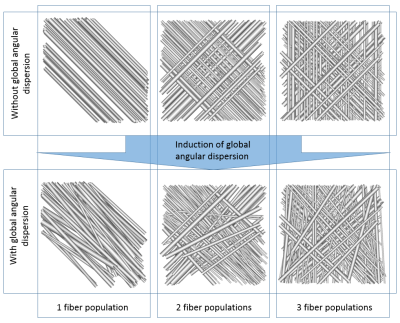
Figure 4 represents configurations with one, two and three populations with or without global angular dispersion (AD). The target $$$10°$$$ AD value is reached only in the single population case, showing that the use of tortuosity is essential to reach high values of AD in multiple population configurations since the maximum attainable global AD strongly depends on the number of fiber populations. Indeed, in figure 5.2, global AD enables to reach $$$5.6°$$$ of AD (for a target of $$$10°$$$). The tortuosity induction (5.3) brings this AD up to the $$$10°$$$ target . Figure 5.4-5 illustrate the creation of myelin sheath and Ranvier nodes, accounting for the actual structure of myelinated fibers8,9. Beadings -appearing in ischemia10- are also handled in figure 5.6, which presents a biomimicking geometry combining all the putative deformations of membranes observed in real tissues.

Discussion & Conclusion

A novel tool to design more realistic WM phantoms was presented, showing the possibility to generate WM biomimetic meshes (including crossing regions) using few parameters. The purpose of those biomimetic phantoms is to perform dMRI data synthesis in order to obtain ground truth data and eventually construct dictionaries of simulated geometries to decode WM microstructure. It is unclear whether the synthesized diffusion signal will be sensible to all the modeled features (Ranvier nodes for instance). Further work will consist in characterizing this sensitivity, as well as the effect of other geometries which are not taken into account in analytical models, such as the presence of mitochondria and oligodendrocytes, which could slow down the diffusion in the intra- and extra-axonal spaces, respectively.

Acknowledgements

This project has received funding from the European Union's Horizon 2020 Framework Programme for Research and Innovation under Grant Agreement No 720270 (Human Brain Project SGA1).

References

1. Assaf, Y., Blumenfeld-Katzir, T., Yovel, Y., and Basser, P. J. (2008). Axcaliber: a method for measuring axon diameter distribution from diffusion MRI. Magnetic resonance in medicine 59, 1347–1354.

2. Zhang, H., Schneider, T., Wheeler-Kingshott, C. A., and Alexander, D. C. (2012). Noddi: practical in vivo neurite orientation dispersion and density imaging of the human brain. Neuroimage 61,1000–1016.

3. Neher, P. F., Laun, F. B., Stieltjes, B., & Maier‐Hein, K. H. (2014). Fiberfox: facilitating the creation of realistic white matter software phantoms. Magnetic resonance in medicine, 72(5), 1460-1470.

4. Hall, M.G. and Alexander, D.C. (2009). Convergence and parameter choice for Monte-Carlo simulations of diffusion MRI., IEEE Transactions on Medical Imaging, Vol. 28, 1354-1364.

5. Yeh, C.-H., Schmitt, B., Le Bihan, D., Li-Schlittgen, J.-R., Lin, C.-P., and Poupon, C. (2013). Diffusion Microscopist Simulator: a general Monte-Carlo simulation system for diffusion magnetic resonance imaging. PloS one 8, e76626.

6. Wedeen, V. J., Rosene, D. L., Wang, R., Dai, G., Mortazavi, F., Hagmann, P., ... & Tseng, W. Y. I. (2012). The geometric structure of the brain fiber pathways. Science, 335(6076), 1628-1634.

7. Axer, H., Axer, M., Krings, T., & Keyserlingk, D. G. V. (2001). Quantitative estimation of 3-D fiber course in gross histological sections of the human brain using polarized light. Journal of neuroscience methods, 105(2), 121-131.

8. Rushton, W. A. H. (1951). A theory of the effects of fibre size in medullated nerve. The Journal of physiology, 115(1), 101-122.

9. Salzer, J. L. (1997). Clustering sodium channels at the node of Ranvier: close encounters of the axon–glia kind. Neuron, 18(6), 843-846.

10. Budde, M. D. and Frank, J. A. (2010). Neurite beading is sufficient to decrease the apparent diffusioncoefficient after ischemic stroke. Proceedings of the National Academy of Sciences 107, 14472–14477.

Figures

Figure 1 : a. Phantom generation for two populations (blue and green) with orientations $$$u_i$$$ b. Global angular dispersion is created by selecting randomly an axon among a given fiber and a point on this axon which will be the center of rotation of the fiber. The selection of the rotation center follows a Gaussian distribution with mean $$$\mu$$$ and variance $$$\sigma$$$. A perturbation vector $$$g$$$ whose components follow a Gaussian distribution with a variance proportional to the target angular dispersion is added to the orientation vector $$$u$$$, resulting in a rotation around the selected fixed point and in a new orientation vector $$$u'$$$.

Figure 2 : a. Local angular dispersion is induced by deforming each axon separately. A point on the axon (in red) and a direct trieder ($$$u_x, u_y, u_z$$$) are chosen randomly. $$$u_y$$$ defines the direction of the tortuosity deformation whose amplitude follows a Gaussian distribution with a variance depending on the number of points which are affected by the deformation around the central red point. b. Creation of the myelin sheath. Inside each cylinder of radius $$$R_{tot}$$$, an inner cylinder of radius $$$R=g.R_{tot}$$$ ($$$g$$$ is the g-ratio) is created which represents the axonal membrane, and the external cylinder represents the outer layer of myelin sheath.

Figure 3: a. Creation of Ranvier nodes. The resolution of the fiber mesh around each Ranvier node is refined to better account for the exponential decay of the myelin thickness around the node. b. Beading generation. Both the axonal contour (inner mesh) and the myelin sheath (external mesh) are swollen with a sine function. The myelin sheath thickness is preserved since beading comes from the swelling of the axonal membrane due to injury.

Figure 4 : Up. Surface renderings of outer fiber envelopes corresponding to one (left), two (middle) and three (right) fiber populations with intracellular fraction of 0.06 for one population, 0.03 each for the two populations, 0.02 each for the three populations and mean diameters 2.5 µm (one population), 1.5 and 2.5 µm (two populations), 1.5, 2.0 and 2.5 µm (three populations). Down. Same as Up. with global angular dispersion (AD) of 10° for the single population, 5.5° and 8.5° for the two populations, 5.5°, 6.7° and 8.5° for the three populations (for a target AD of 10° each).

Figure 5 : 1. Surface renderings corresponding to three fiber populations with mean diameters 1.5, 2.0 and 3.0 µm respectively with intracellular volume fraction of 0.05 each. N is the number of populations in general (here N=3). 2. Global angular dispersion is induced (4.7°, 2.5° and 2.8° per population). 3. Tortuosity is induced, enabling to reach 10° of angular dispersion for each population. 4. Creation of the myelin sheath. 5. Creation of Ranvier nodes with mean ratio 1000 between internodal length and node width. 6. Creation of beadings with 20.0 µm mean inter-beading length and beading magnitude ratios of 1.7, 1.5 and 1.2 respectively.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
3099