3065
Super-resolution Hyperpolarized C13 Imaging with 2D-Linear Prediction and Trigonometric Curves1Oxford Centre for Clinical Magnetic Resonance Research, University of Oxford, Oxford, United Kingdom, 2Department of Physics, University of Oxford, Oxford, United Kingdom, 3Department of Physiology, Anatomy and Genetics, University of Oxford, Oxford, United Kingdom
Synopsis
Hyperpolarized $$$^{13}\text{C}$$$-imaging techniques a powerful and clinically translatable method to image metabolism. However, owing to the finite and non-renewable magnetisation available to the technique, all proposed imaging sequences necessarily have a comparatively small matrix size compared to conventional anatomical imaging. Typically hyperpolarized images are therefore reconstructed with a large degree of zero-filling. We show here that a modified form of 2D least-squares linear prediction that uses the known analytic properties of trigonometric curves can extrapolate unmeasured Fourier coefficients and hence improve the apparent reconstructed resolution of hyperpolarized images.
Purpose
Hyperpolarized $$$^{13}\text{C}$$$-imaging methods hold enormous promise as a new metabolic imaging technique and are, with [1-$$$^{13}$$$C]pyruvate, translating to the clinic.[1,2] However, the combination of a limited $$$T_2$$$ and the finite and non-renewable magnetisation inherent to all hyperpolarized experiments necessarily limits the achievable matrix size of any imaging acquisition that could be performed, typically to $$$16\times16,\,32\times32$$$ or similar. As comparable anatomical imaging matrices are substantially larger, and such images are subject to severe partial volume effects, it is therefore common to zero-fill the acquired data by a factor of $$$2^{1\rightarrow4}$$$. This corresponds directly to a sinc-shaped interpolation in the image domain.
Several methods have been proposed to recover higher spatial frequency information than that acquired in MR, most famously 1D linear prediction for FIDs,[3,4] and compressed sensing. However, modern compressed sensing methods require sparsity that may be difficult to guarantee with small matrix sizes and often require nonuniform sampling at acquisition time in $$$k$$$-space for acceleration.[5,6] Although compressed sensing approaches have been previously proposed with hyperpolarized MRI, the undersampling regime has typically been one dimensional and limited to a small number of points on the extremities in $$$k$$$-space, in part owing to gradient fidelity limitations and the breakdown of the sparsity assumptions with small matrix sizes.[7]
As an alternative, we propose here the use of a method for analytically extending acquired samples into the Fourier domain that is traditionally viewed as too computationally intensive for use with larger matrix sizes, as commonly found on proton imaging.
Methods
Following the novel approach proposed by Ongie and Jacob,[8] we assume that hyperpolarized images are piecewise-constant apart from a finite number of edges. It has been shown that these edges obey an annihilation relation with a finite subset of trigonometric curves that can be uniquely determined under certain conditions. We use the analytic properties of this fact to perform a least-squares linear prediction of the acquired Fourier samples to new parts of the complex domain. That is, if $$$I(\mathbf{x})$$$ is a (fully-sampled) MR image, and $$$f(\mathbf{x})=\mathcal{FT}(\mathbf{x})$$$ its $$$k$$$-space, then $$$\exists c[\mathbf{k}]$$$ defining a trigonometric curve $$$\mu$$$ such that
\begin{align}\mu(\mathbf{x})\nabla{}f(\mathbf{x}) &=0,\quad\,\text{where for a finite image}\\ \mu(\mathbf{x}) &= \sum_{\mathbf{k}\in\Lambda}c[\mathbf{k}]e^{2\pi i\mathbf{k}\cdot\mathbf{x} },\quad\text{given}\,\,c[\mathbf{k}]\in\mathbb{C},\,\text{and}\,\,\Lambda\subset\mathbb{Z}^2,\,\,|\Lambda|\in\mathbb{N}.\end{align}
It can be shown that if, instead of acquiring a fully-sampled image $$$I$$$, we obtain only a few (low) spatial frequencies of $$$f$$$ given as
\begin{align} \widehat{f[\mathbf{k}]}=\int I(\mathbf{r}) e^{-2\pi i\mathbf{k}\cdot\mathbf{r}} \,\text{d}\mathbf{r},\quad\mathbf{k}\in\Gamma\subset\mathbb{Z}^2\end{align}
then this annihilation condition corresponds to a finite system of linear equations
\begin{align} \sum_{\mathbf{k}\in\Lambda}c[\mathbf{k}]\widehat{\nabla f}[\boldsymbol{\ell}-\mathbf{k}] =0, \quad\forall\boldsymbol{\ell}\in2\Lambda.\end{align}
Furthermore, under a set of assumptions discussed in detail elsewhere,[8] $$$c[\mathbf{k}]$$$ can be recovered from the acquired data through convolution with a filter derived from the data itself, leading to a Toeplitz operator $$$\mathcal{T}\subset \mathbb{C}^2$$$ such that $$$\mathcal{T}c[\mathbf{k}]=0$$$ that is obtained after the data are subject to a Cadzow denoising step that requires the SVD of a large matrix. This gives rise to a Tikunhov-regularised minimisation problem for the unknown Fourier samples beyond the grid of those acquired, namely
\begin{align}\text{argmin}_{\hat{f}[\mathbf{k}]}\left|\left|\mu\nabla\hat{f}[\mathbf{k}] \right|\right|_{2}^{2} + \lambda\left|\left| P_\Gamma\left( \frac{\hat{f}[\mathbf{k}]+\mathcal{T}^*\mathcal{T}}{1+\lambda\text{diag}(\mathcal{T}^*\mathcal{T})} -c[\mathbf{k}] \right) \right|\right|^{2}_{2} \end{align}
where $$$\lambda$$$ is a regularisation parameter and $$$P_\Gamma$$$ a projection operator onto the new resampling space. This process takes several minutes on a modern CPU with $$$32\times32\times16$$$ matrix sizes, owing to the dimensions of $$$\mathcal{T}$$$, and does not scale well with matrix size.
Results
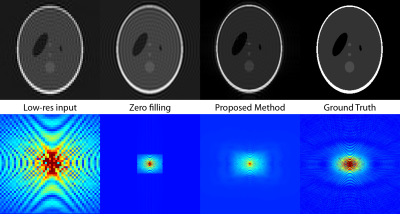
Fig. 1 shows the Fourier and image domain for a $$$256\times256$$$ Shepp-Logan phantom downsampled to $$$49\times65$$$ and reconstructed either via zero-filling or the proposed 2D Least Squares Linear Prediction method. Gibbs ringing is substantially ameliorated. Fig. 2 show the results of the method applied to real data obtained from the in vivo healthy rat heart through a 3D-Spectral Spatial EPI sequence[9,10] with a $$$32\times32\times12$$$ matrix size. The method was applied in-plane. Rows represent the metabolites pyruvate, bicarbonate and lactate, and the $$$z$$$-axis is shown concatenated.Discussion
We have shown that the necessarily small matrix size inherent to X-nuclei imaging lends itself well to reconstruction methods beyond zero filling. In particular, 2D least-squares linear prediction is known to be preferable compared to other methods for extrapolating regularly spaced Fourier samples beyond their original grid, albeit at a computational cost that may be prohibitive for higher matrix size applications as it necessitates the SVD of a large (i.e. $$$\mathcal{O}\left(10^{4\rightarrow5}\right)$$$) matrix. We have demonstrated that the method works in vivo, and can reconstruct images with a higher apparent SNR and spatial resolution than the conventional approach.Conclusions and Future Work
Future work will implement generalised forms of the method to enable 3D reconstructions, explore its numerical stability to noise, and investigate its utility in other forms of X-nuclei imaging.Acknowledgements
JJM would like to acknowledge the financial support of the Novo Nordisk Foundation, the British Heart Foundation and EPSRC.References
[1] C. H. Cunningham, J. Y. Lau, A. P. Chen, B. J. Geraghty, W. J. Perks, I. Roifman, G. A. Wright, K. A. Connelly, Circ. Res. 2016, CIRCRESAHA.116.309769.
[2] S. J. Nelson, J. Kurhanewicz, D. B. Vigneron, P. E. Z. Larson, A. L. Harzstark, M. Ferrone, M. van Criekinge, J. W. Chang, R. Bok, I. Park, G. Reed, L. Carvajal, E. J. Small, P. Munster, V. K. Weinberg, J. H. Ardenkjaer-Larsen, A. P. Chen, R. E. Hurd, L.-I. Odegardstuen, F. J. Robb, J. Tropp, J. A. Murray, Sci. Transl. Med. 2013, 5, 108.
[3] G. Zhu, A. Bax, J. Magn. Reson. 1990, 90, 405–410.
[4] H. Gesmar, J. J. Led, J. Magn. Reson. 1988, 76, 183–192.
[5] M. Lustig, D. Donoho, J. M. Pauly, Magn. Reson. Med. 2007, 58, 1182–1195.
[6] M. Lustig, D. L. Donoho, J. M. Santos, J. M. Pauly, Compressed sensing MRI: A look at how CS can improve on current imaging techniques, 2008.
[7] B. J. Geraghty, J. Y. Lau, A. P. Chen, C. H. Cunningham, Magn. Reson. Med. 2017, 77, 538–546.
[8] G. Ongie, M. Jacob, SIAM J. Imaging Sci. 2016, 9, 1004–1041.
[9] J. J. Miller, A. Z. Lau, D. J. Tyler, Magn. Reson. Med. 2017, DOI 10.1002/MRM.26839.
[10] J. J. Miller, A. Z. Lau, I. Teh, J. E. Schneider, P. Kinchesh, S. Smart, V. Ball, N. R. Sibson, D. J. Tyler, Magn. Reson. Med. 2015, 75, 1515–1524.
Figures