2993

Improved Non-Contrast Renal Angiography Using Respiratory and Cardiac Gating with Dynamically Determined Inversion Times: A Simulation Study
Xiaoxuan He1, Naoharu Kobayashi1, Xiufeng Li1, and Gregory J. Metzger1

1Center for Magnetic Resonance Research, University of Minnesota, Minneapolis, MN, United States

Synopsis

In this simulation study, we aim to demonstrate the feasibility of improving non-contrast enhanced renal MRA by adding a cardiac gate with dynamically determined inversion times. The benefits of the proposal include higher contrast due to better background suppression and improved inflow enhancement, which may be clinically significant for delineating occluded vessels.

Introduction

Non-contrast enhanced (non-CE) renal MRA has been shown to benefit from higher field due to improved SNR and better inflow enhancement1. However, the inversion recovery (IR) prepared turbo-FLASH acquisition triggered by a respiratory gate with a static inversion time (TI) may suffer from degraded background tissue suppression, due to respiratory rate variability. The timing of inversion pulse may also limit the inflow enhancement which is dependent on the heart rate2. In this study, we demonstrate by simulation the feasibility and advantages of a novel acquisition strategy with a cardiac gate and a dynamic TI to address these problems.

Methods

- Renal Phantom Design

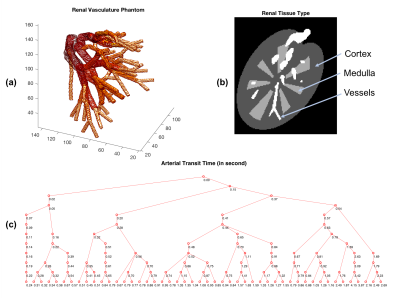
A numerical renal phantom was designed to simulate the arterial vasculature, flow and magnetization states. The renal vasculature was represented by a tree structure, where each node, denoted by a 3D coordinate estimated from a renal MR angiography dataset acquired at 7.0 Tesla1, represented a curvature, bifurcation or trifurcation site in the arteries. For each node and its parental node, a vessel branch along with its radius, flow and magnetization information was defined. A total of 121 nodes were defined in the phantom, with the estimated arterial transit times shown in Figure 1a,c. The cortex and medulla were modeled to mimic actual geometry and were given assigned previously determined T1 values3 (Figure 1b). In the methods below, the TI was optimized to suppress the cortex as practically the medulla has much lower signal due to its relatively short T2* which was not currently modeled4.

- Gating Logics

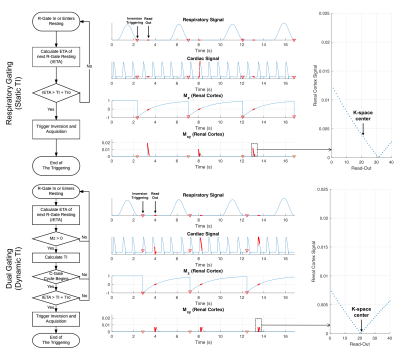
The respiratory signal was synthesized by a series of normalized cosine waves. The cardiac signal was synthesized by a series of simulated renal blood flow waveforms5 instead of ECG. The conventional sequence triggers inversion pulse with a static TI when the respiratory signal descends below a certain threshold1. For the proposed method, the inversion pulse is dynamically triggered right before a cardiac cycle with a dynamic TI. Detailed gating logics are shown in Figure 2.

- Fluid Dynamics Computation

A zero-dimensional lumped model was used to describe the blood flow dynamics along with the assumption that all vessels are cylindrical rigid pipes filled by incompressible blood with laminar resistance. Given the renal blood inflow waveform, the flow rate in each vessel was calculated by solving its electrical current in an equivalent electrical circuit with known resistance and current source6. The vasculature was tuned to have a wide range of flow rate to represent both unobstructed flow and occlusion.

- MR Image Formation

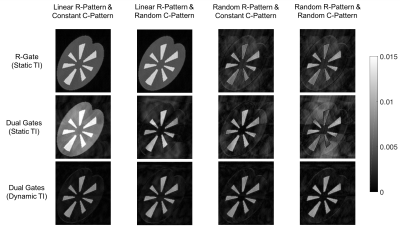
Based on the timing of pulses from the gates, the time variant phantom signals were calculated by Bloch equations and used to simulate image acquisition. A 3D GRE readout simulation with flow compensation and spoiling gradient was used to acquire the K-space with flip angle 8°, acquisition matrix 80 x 70 x 90, Turbo Factor 40. Three different gating strategies were used for simulation: 1) Respiratory gating only with a static TI. 2) Respiratory and cardiac gating with a static TI. 3) Respiratory and cardiac gating with a dynamic TI. To compare the performance under various respiratory and cardiac patterns, we evaluated the following combinations: 1) constant cardiac cycle (0.8s) and linearly increasing respiratory cycle (3s to 5s). 2) uniformly distributed cardiac cycle (0.8s to 1.0s) and linearly increasing respiratory cycle (3s to 5s). 3) constant cardiac cycle (0.8s) and uniformly distributed respiratory cycle (3s to 5s). 4) uniformly distributed cardiac cycle (0.8s to 1.0s) and uniformly distributed respiratory cycle (3s to 5s).

- Contrast Comparison

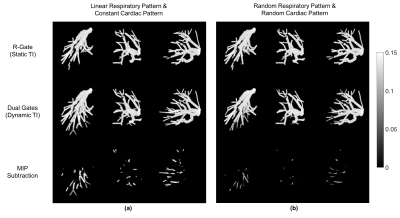
A contrast ratio (CR), defined as the ratio between estimated vessel signal and measured mean tissue signal, was calculated and normalized to evaluate the suppression of cortex and medulla quantitatively. For the inflow enhancement comparison, a subtraction of maximum intensity projection (MIP) image between dynamic TI and static TI was calculated to show the vessel signal difference.

Results

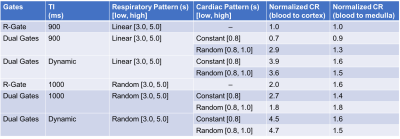
The proposed dual gate triggering with a dynamic TI improved the relative contrast ratio to cortex by approximately two to four-fold (See Table 1, Figure 3). It also improved visibility in some vessels as observed in the subtracted MIP images (See Figure 4).

Discussion

Our simulations demonstrate that cardiac gating the inversion pulse can improve contrast by maximizing inflow enhancement, which may be clinically important for identifying occluded vessels with an arterial transit time sensitive to TI. While the timing variability might degrade background tissue suppression and cause potential artifact, they can be significantly lessened by introducing a dynamic TI which can also address variations in respiratory rate.

Conclusion

The dual gate triggering with dynamic TI can improve contrast and occluded vessel visibility by optimally suppressing tissue signal and maximizing inflow enhancement.

Acknowledgements

In addition to grant support, NIBIB P41 EB015894, the authors would like to thank Mostafa Toloui for helping with fluid dynamics computation, and Seng-Wei Chieh for the discussion about MR image formation simulation.

References

1. Metzger, G. J. et al. Dynamically applied B1+ shimming solutions for non-contrast enhanced renal angiography at 7.0 Tesla. Magn Reson Med 69, 114–126 (2013).

2. Liu, X. et al. Renal Transplant: Nonenhanced Renal MR Angiography with Magnetization-prepared Steady-State Free Precession. Radiology 251, 535–542 (2009).

3. Li, X., Bolan, P. J., Ugurbil, K. & Metzger, G. J. Measuring renal tissue relaxation times at 7 T. NMR Biomed. 28, 63–69 (2015).

4. Li, X., Auerbach, E. J., Moortele, P. Van De, Ugurbil, K. & Metzger, G. J. Multi-Parametric Renal MRI at 7T. in Proceedings of the 23rd Annual Meeting of ISMRM, Toronto, Ontario, Abstract 6584 (2015).

5. Liang, F. & Liu, H. A Closed-Loop Lumped Parameter Computational Model for Human Cardiovascular System. JSME Int. J. Ser. C 48, 484–493 (2005).

6. Kokalari, I., Karaja, T. & Guerrisi, M. Review on lumped parameter method for modeling the blood flow in systemic arteries. J. Biomed. Sci. Eng. 6, 92–99 (2013).

Figures

Figure 1. The numerical renal phantom designed in the study with an isotropic 0.5 mm voxel size. (a) a 3D view of the vasculature. (b) one axial slice with cortex, medulla and arteries. (c) the mean arterial transit time of each vessel shown in a tree structure that defines the vasculature hierarchy. The renal blood flow is assumed to be 800 mL/min. The vasculature is tuned to have a wide range of arterial transit times to represent both unobstructed flow and occlusion.

Figure 2. Flow charts and timing graphs of gating logics for dual gate triggering with dynamic TI and respiratory gate only triggering with static TI. R-Gate: respiratory gate; C-Gate: cardiac gate; rETA: estimated time of arrival of next respiration; Tro: total time of read-out. Two advantages of a dynamic TI can be appreciated from this figure: 1) the cortex signal is better suppressed (see right insets where cortical signal is appropriately nulled at the K-space center) and 2) with optimal timing it is more likely that a second cardiac cycle can occur between inversion and readout thus increasing inflow enhancement.

Table 1. The normalized contrast ratio (CR) of the blood signal to the cortex and medulla for each combination of respiratory and cardiac patterns. All CR values are normalized by the first row of the table. The physiologic cycles in the random patterns referred to in the table are all uniformly distributed within the given ranges (low, high). The linear patterns vary linearly (low, high). In the random case the static TI is calculated based on the average steady-state magnetization with respect to the given respiratory pattern.

Figure 3. Comparison of renal tissue suppression between the three different gating strategies (i.e. R-gate, Dual Gate static TI and Dual Gate dynamic TI) with 4 different patterns of respiratory (R) and cardiac (C) variations. A good result in this simulation is a fully suppressed cortex with minimal background artifact for all variations of the cardiac and respiratory patterns. The persistent signal from the medulla is acceptable as it has a longer R2* and typically is not observed as a confounding factor in vessel delineation.

Figure 4. Comparison of reconstructed vasculature using maximum intensity projection (MIP) with respiratory gating and static TI versus dual triggering with dynamic TI. Results of two combinations of respiratory and cardiac cycles are shown: (a) linearly increasing respiratory cycle and constant cardiac cycle. (b) random respiratory and cardiac cycles both uniformly distributed.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
2993