Synopsis

Vessel-selective ASL angiography provides information about cerebral blood supply not achievable by other non-invasive techniques. It is, however, limited by long acquisition times. Here we demonstrate the benefit of using compressed sensing to reconstruct undersampled vessel-selective angiograms and furthermore, consider how the vessel-encoding process affects the choice of sampling strategy compared to non-selective imaging. We show that vessel-selective angiograms arising from three brain-feeding arteries can be reconstructed with excellent fidelity in the same scan time normally required for non-selective ASL angiography.

Introduction

Vessel-selective angiograms provide crucial information about brain blood supply (e.g. evaluating collateral blood flow or blood supply to lesions). Such images can be obtained non-invasively using Vessel-Encoded Arterial Spin Labelling (VE-ASL)^1,2. However, vessel-encoding increases scan times compared to standard ASL angiography, reducing its utility in clinical environments.

One method to accelerate imaging is to undersample the data, and use non-linear reconstruction methods to recover the vessel-encoded images. Compressed sensing (CS) approaches enable undersampled image recovery by exploiting image sparsity^3-5, and while conventional angiograms are inherently sparse, vessel-selective angiograms are even sparser, so are ideal for reconstruction with CS.

Here we present a novel framework for the reconstruction of VE-ASL angiograms using CS, consider different sampling strategies across encoding cycles, and show the feasibility of obtaining vessel-selective images in the same time normally required for a non-selective acquisition.

Methods

Five fully sampled 3D vessel-selective angiograms⁶ were used as ground truth for evaluation of the reconstruction method. The images were re-encoded using a 4x4 Hadamard matrix, and under-sampled by randomly selecting 50% of the lines of the Cartesian k-space.

With 50% sampling, three arteries encoded by four VE-ASL cycles can be acquired in the same scan time as non-selective ASL⁷. The encoding process can be described via the linear relationship:$$\begin{gathered}\mathbf{y=}\mathbf{A}\mathbf{x}\\\mathbf{y=}\left[\begin{array}{c}y_1\\y_2\\y_3\\y_4\end{array}\right],\mathbf{A=}\left[\begin{array}{rrrr}-1&1&-1&1\\1&-1&-1&1\\-1&-1&1&1\\1&1&1&1\end{array}\right],\mathbf{x=}\left[\begin{array}{c}R\\L\\B\\S\end{array}\right]\end{gathered}$$Where $$$\mathbf{y} $$$ contains the vessel-encoded signal, $$$\mathbf{A}$$$ is the encoding matrix (-1 representing tagging, and 1 control) and $$$\mathbf{x}$$$ contains the signal from each component (right internal carotid (R), left internal carotid (L), basilar artery (B), and static tissue (S)).

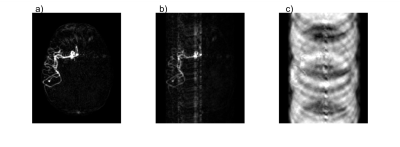
When undersampling and reconstructing by zero-padding the k-space of $$$\mathbf{y}$$$, decoding using $$$\mathbf{A}^{-1}$$$ results in aliasing in $$$\mathbf{x}$$$, where the aliasing characteristics depend on the sampling strategy used (Figure 1). For simplicity, one sampling pattern was used across all encodings in this work.

CS regularises the least-squares problem with the L₁-norm of the data in its sparse domain, using the following cost function: $$f(\mathbf{x})=\frac{1}{2}||\mathbf{Ex}-\mathbf{d}||_2^2+\lambda||\mathbf{x}||_1$$ where $$$\mathbf{x}$$$ is the sparse vessel-encoded angiogram ($$$\mathbf{x}=\mathbf{A}^{-1}\mathbf{y}$$$) and $$$\mathbf{E}$$$ is the acquisition matrix that brings the sparse images ($$$\mathbf{x}$$$) to the same domain as the acquired data ($$$\mathbf{d}$$$). For vessel-encoded angiograms $$$\mathbf{E}=\mathbf{FA}$$$, where $$$\mathbf{A}$$$ is the encoding matrix defined above and $$$\mathbf{F}$$$ is an undersampled Fourier transform. $$$\lambda$$$ is a scale-dependent regularisation factor, and was set to 0.01 in these reconstructions.

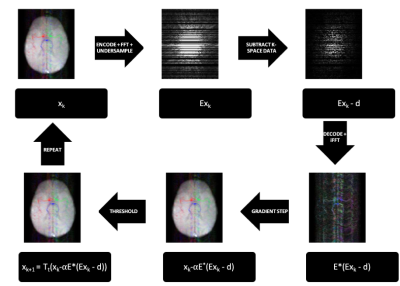
The cost function was minimised using an iterative soft thresholding algorithm (ISTA) implemented in MATLAB (Figure 2). ISTA eliminates true noise present in the data as well as noise-like aliased signal. Therefore, in order to better assess residual aliasing artefacts, the reconstructed images were compared to both the original and denoised versions of the ground truth. Denoising was performed by running the images through the same ISTA algorithm used for reconstruction, but without undersampling.

A structural similarity index (SSIM)⁸ that ranges from 0 (least similar) to 1 (most similar) was used as a performance metric, calculated over local neighbourhoods with a Gaussian weighting kernel with a standard deviation of 1.5 voxels.

Results

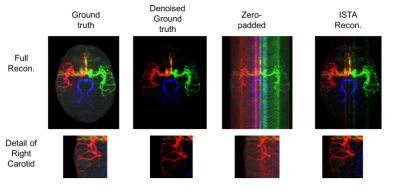
The proposed algorithm reconstructs the angiograms to a qualitatively good result (Figure 3).

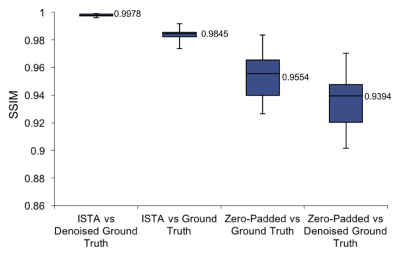
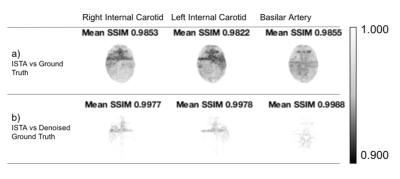
Figure 4 summarises average SSIM across images for ISTA against the noisy and denoised ground truth, and shows a clear improvement over the zero-padded reconstruction.

The accumulation of low SSIM values for ISTA compared to the original ground truth was mainly outside the vessels (Figure 5a). Therefore, ISTA compared to the denoised ground truth had the highest SSIM values due to the reduction of background noise (Figure 5b), highlighting the denoising effect of ISTA.

Discussion

The proposed reconstruction approach leverages the considerable sparsity of VE-ASL angiograms to yield vessel-selective images arising from three brain-feeding arteries in the same time required for a conventional non-selective ASL angiogram. The visual quality of the results and high SSIM values are promising.

The considerable similarity between the ISTA reconstruction (based on inherently noisy real data) and the denoised ground truth suggests that the method is robust to noise. However, further simulations and prospectively undersampled acquisitions are needed to evaluate robustness to noise further.

In this work, the same k-space sampling pattern was applied across all vessel-encoded cycles. However, the complimentary information available across different encodings could potentially be better utilised if different sampling patterns were used. Alternatively, the framework could be extended to time-resolved data: varying sampling patterns across the time-resolved images and constraining the temporal signal evolution would leverage the mutual information without the mixing of aliased components.

Overall, the initial results look promising and by extending the framework, undersampled VE-ASL moves towards being a clinically useful tool for assessment of cerebrovascular disease.

Acknowledgements

References

1. Wong, E. C. Vessel-encoded arterial spin-labeling using pseudocontinuous tagging. Magn. Reson. Med. 58, 1086–1091 (2007).

2. Okell, T. W. et al. Vessel-encoded dynamic magnetic resonance angiography using arterial spin labeling. Magn. Reson. Med. 64, 430–438 (2010).

3. Donoho, D. L. Compressed sensing. IEEE Trans. Inf. Theory 52, 1289–1306 (2006).

4. Lustig, M., Donoho, D. L., Santos, J. M. & Pauly, J. M. Compressed Sensing MRI. IEEE Signal Process. Mag. 25, 72–82 (2008).

5. Lustig, M., Donoho, D. & Pauly, J. M. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn. Reson. Med. 58, 1182–1195 (2007).

6. Okell, T. W. et al. Optimization of 4D vessel-selective arterial spin labeling angiography using balanced steady-state free precession and vessel-encoding. NMR Biomed. 29, 776–786 (2016).

7. Günther, M. Efficient visualization of vascular territories in the human brain by cycled arterial spin labeling MRI. Magn. Reson. Med. 56, 671–675 (2006).

8. Wang, Z., Simoncelli, E. P. & Bovik, A. C. Multiscale structural similarity for image quality assessment. in The Thrity-Seventh Asilomar Conference on Signals, Systems Computers, 2003 2, 1398–1402 Vol.2 (2003).