2977

High-resolution Imaging with a priori Knowledge Incorporating the Navier-Stokes equations and the discontinuous Galerkin method (4D flow HIKING): towards flow reconstruction constrained by computational fluid dynamics
Johannes Töger1, Matthew J Zahr2, Karin Markenroth Bloch3, Marcus Carlsson4, and Per-Olof Persson2

1Diagnostic Radiology, Department of Clinical Sciences, Skane University Hospital, Lund University, Lund, Sweden, 2Department of Mathematics, Lawrence Berkeley Laboratory and University of California, Berkeley, CA, United States, 3Lund University Bioimaging Center, Lund University, Lund, Sweden, 4Clinical Physiology, Department of Clinical Sciences, Skane University Hospital, Lund University, Lund, Sweden

Synopsis

Magnetic resonance 4D flow imaging is a promising technique for diagnosis and follow-up of disease. However, 4D flow is limited by long scan times and low resolution. This work presents phantom validation of a new method for 4D flow scan acceleration, called 4D flow high-resolution imaging with a priori knowledge incorporating the Navier-Stokes equations and the discontinuous Galerkin method (4D flow HIKING). Excellent agreement with laser particle image velocimetry (PIV) was found, demonstrating the potential of the framework for scan time reduction and enhanced data quality in 4D flow.

Background

Recent accelerated MRI methods exploit a priori information, e.g. spatiotemporal correlations (1) or sparsity (2). The Navier-Stokes equations describe blood flow physics accurately and can therefore give valuable a priori information for 4D flow, promising increased data quality and/or reduced scan times. However, previous Navier-Stokes 4D flow reconstruction methods are limited by simplified treatment of the Navier-Stokes equations (3) and insufficient modelling of spatiotemporal smoothing in MRI (4).

We have recently developed a 4D flow reconstruction framework, called 4D flow high-resolution imaging with a priori knowledge incorporating the Navier-Stokes equations and the discontinuous Galerkin method (4D flow HIKING), including a high-order computational fluid dynamics (CFD) solver and a spatiotemporal smoothing model. Therefore, this study aims to 1) validate 4D flow HIKING in a phantom setup with laser particle image velocimetry (PIV) as the reference standard and 2) investigate the performance of 4D flow HIKING in the presence of noise and low resolution in synthetic 2D data.

Methods

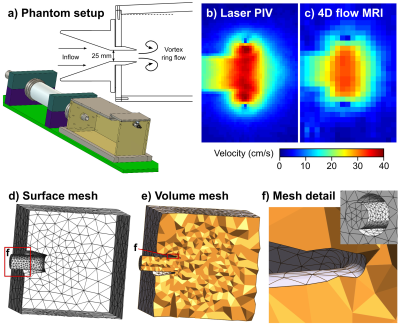
For the phantom validation, a previously presented setup based on vortex ring formation was used (5) (Figure 1). A pulsatile pump drives flow through a 25 mm nozzle to generate vortex rings, a highly repeatable flow condition modelling diastolic flow in the human heart (6).

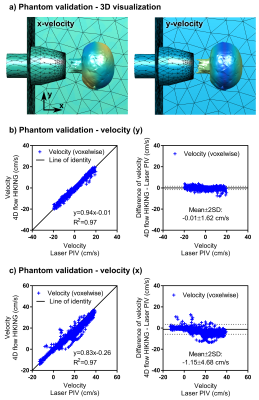
A computational mesh with approximately 50,000 tetrahedral elements (p=2) was used for the 4D flow HIKING reconstruction (Figure 1d-f, Figure 2a). The input data to the 4D flow HIKING reconstruction consisted of the computational mesh and low-resolution 4D flow data obtained using conventional SENSE reconstruction (Philips Achieva 1.5T, Best, The Netherlands) (5). The inflow in the tank nozzle was assumed to be constant over the nozzle, and parameterized by a Gaussian profile in time yielding 3 parameters to be optimized for: the Gaussian’s center (pulse timing), standard deviation (pulse width) and the peak flow rate. The accuracy of the 4D flow HIKING reconstruction was evaluated by comparing velocity values voxel-by-voxel to laser particle image velocimetry (PIV) data obtained in the same phantom setup.

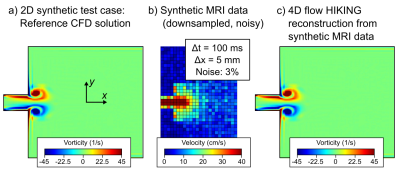
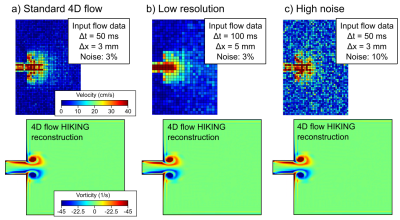
For the synthetic tests, a reference CFD solution in a two-dimensional (2D) geometry was computed (Figure 3). The reference solution was then downsampled (Figure 1b) with added noise to provide simulated MRI data corresponding to a) a consensus 4D flow sequence (7), b) low-resolution conditions, and c) high-noise conditions (Figure 4).

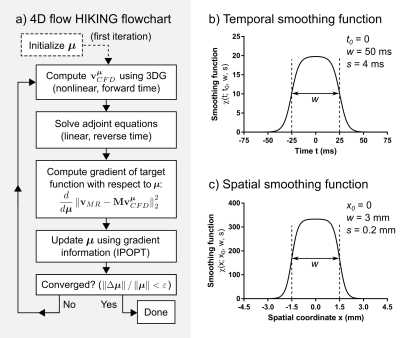
Low-resolution data and a mesh describing the flow domain were used as input to the HIKING framework, which is based on three main components (Figure 5): 1) a target functional measuring the similarity between the MR flow data and CFD solution, linked by the forward model M, 2) the 3DG CFD solver (8), which computes the CFD solution from boundary conditions encoded in the parameter vector µ, and 3) the adjoint equations (8), used to compute the gradient of the target functional. The target functional is then minimized iteratively using the IPOPT library (9) to reconstruct the high-resolution flow that provides a best-fit to the MRI data.

Results

Phantom validation showed very strong agreement between the 4D flow HIKING reconstruction and the laser PIV reference data (Figure 2). Convergence was attained after 40 hours (14 iterations) on a 16-core computer (~640 CPU-hours).

Synthetic test cases showed excellent performance of the 4D flow HIKING framework (Figure 4). Convergence was attained for each synthetic test case after 220 minutes (55 iterations) on a 16-core computer (~60 CPU-hours per case).

Discussion

The phantom validation demonstrates the ability of 4D flow HIKING of reconstructing fully three-dimensional and time-resolved complex flows. The simple model for the inflow consisted of only three parameters, but yielded excellent agreement with laser PIV data. For a more complex flow scenario, e.g. intracranial flow in the Circle of Willis, a more detailed parameterization may be used (at the cost of increased reconstruction time).

The low-resolution two-dimensional synthetic test corresponds to a spatiotemporal undersampling factor of (5 mm/3 mm)2 × (100 ms/50 ms) ≈ 5.6, while still achieving near-perfect flow reconstruction. This highlights the potential of 4D flow HIKING to reduce 4D flow acquisition times and/or increase data quality.

Conclusion

The 4D flow HIKING framework shows excellent flow reconstruction accuracy compared to laser PIV in a phantom setup. Furthermore, synthetic tests show high potential for acceleration and data quality improvements for 4D flow magnetic resonance imaging.

Acknowledgements

No acknowledgement found.

References

1. Giese D, Wong J, Greil GF, Buehrer M, Schaeffter T, Kozerke S: Towards highly accelerated Cartesian time-resolved 3D flow cardiovascular magnetic resonance in the clinical setting. J Cardiovasc Magn Reson 2014; 16:42.

2. Hsiao A, Lustig M, Alley MT, et al.: Rapid pediatric cardiac assessment of flow and ventricular volume with compressed sensing parallel imaging volumetric cine phase-contrast MRI. Am J Roentgenol 2012; 198:250–259.

3. Rispoli VC, Nielsen JF, Nayak KS, Carvalho JLA: Computational fluid dynamics simulations of blood flow regularized by 3D phase contrast MRI. Biomed Eng Online 2015; 14:110.

4. Funke SW, Nordaas M, Evju Ø, Alnæs MS, Mardal K-A: Variational data assimilation for transient blood flow simulations. arXiv 2016:1607.03013v1.

5. Töger J, Bidhult S, Revstedt J, Carlsson M, Arheden H, Heiberg E: Independent validation of four-dimensional flow MR velocities and vortex ring volume using particle imaging velocimetry and planar laser-Induced fluorescence. Magn Reson Med 2016; 75:1064–1075.

6. Töger J, Kanski M, Arvidsson PM, et al.: Vortex-ring mixing as a measure of diastolic function of the human heart: Phantom validation and initial observations in healthy volunteers and patients with heart failure. J Magn Reson Imaging 2016; 43:1386–1397.

7. Dyverfeldt P, Bissell M, Barker AJ, et al.: 4D flow cardiovascular magnetic resonance consensus statement. J Cardiovasc Magn Reson 2015; 17:72.

8. Zahr MJ, Persson P-O: An adjoint method for a high-order discretization of deforming domain conservation laws for optimization of flow problems. J Comput Phys 2016; 326:516–543.

9. Wächter A, Biegler LT: On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math Program 2006; 106:25–57.

Figures

Figure 1: Phantom validation setup. Panel (a) shows the geometry of the setup. A pulsatile pump drives flow through a 25 mm nozzle, leading to a repeatable vortex ring formation. Panels (b) and (c) show flow data from laser PIV and 4D flow MRI, respectively. Panels (d) and (e) show the computational high-order mesh used for 4D flow HIKING. Panel (f) shows details of the mesh, demonstrating the use of high-fidelity curved tetrahedral finite elements for additional accuracy.

Figure 2: Phantom validation results. Panel (a) shows a 3D visualization of the final 4D flow HIKING reconstruction. Panels (b) and (c) show the agreement between 4D flow HIKING and laser PIV. Excellent agreement was found.

Figure 3: Setup of 2D synthetic numerical tests. Panel a) shows the reference CFD solution. Panel b) shows how synthetic MRI data was constructed by downsampling the CFD data in space and time and adding noise. Panel c) shows the 4D flow HIKING reconstruction of the CFD data from the downsampled, noisy synthetic MRI data.

Figure 4: Results of 2D synthetic tests. Panels a, b and c show 4D flow HIKING reconstruction from downsampled, noisy data. In all three test cases, the reconstruction is very close to the reference CFD solution (Figure 1a).

Figure 5: Technical details. Panel a) shows the 4D flow HIKING method. CFD simulation is performed using the 3DG solver. The spatial discretization is a high-order (p=2 or p=3) Discontinuous Galerkin (DG) method, and the temporal discretization is a 3rd-order implicit Runge-Kutta method. Gradients of the target function with respect to the parameter vector µ are computed using the adjoint equations, enabling efficient updates of µ using the IPOPT framework (9). Panels b) and c) show the temporal and spatial smoothing functions χ used to approximate the 4D flow MRI velocity measurement process in the forward model M.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
2977