Synopsis

The purpose of this study is to develop and extend GRAPPA operator gridding (GROG) for fast iterative reconstruction of radial SMS data, and to compare extended GROG (EGROG) with GROG, Toeplitz and NUFFT methods. Simulation and in-vivo tests were done to compare these methods. Our results show that EGROG improves reconstruction by providing better Cartesian k-space estimation, it outperforms Toeplitz and GROG at oversampling factor 2, and a speed up factor of ~2 was achieved compared to NUFFT.

Introduction

Method

Extending GROG

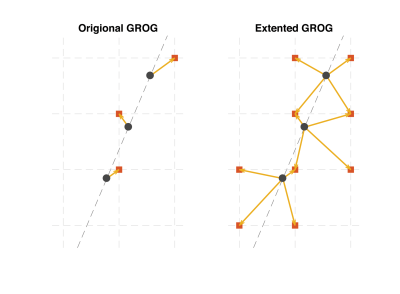
GROG uses estimated operators $$$G_x$$$, $$$G_y$$$ to shift each measured non-Cartesian point to its nearest Cartesian neighbor^3,5. However, as illustrated in Figure 1 this shifting can be extended to a one to more mapping, which can benefit reconstruction by providing an improved estimation of Cartesian k-space.

SMS GROG

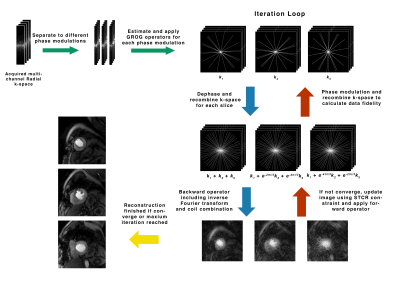
Radial CAIPIRINHA excites and acquires multiple slices simultaneously by adding different phases on radial k-space spokes⁶. This phase modulation changes the correlation within k-space spokes, therefor different GROG operators are required for different phase modulation spokes. After gridding, the Cartesian data were dephased and recombined to generate k-space for each image slice. These steps are incorporated into the sampling matrix $$$A$$$ for iterative reconstruction, such that $$$A = \Phi \mathcal{F} S $$$, where $$$S$$$ represents coil sensitivity maps, $$$\mathcal{F}$$$ is Fourier transform and $$$\Phi$$$ is phase modulation and recombination of k-space. All SMS slices were reconstructed jointly by minimizing:

$$ \left\|Am-d\right\|^2_2 + \lambda_t \left\|\sqrt{\nabla_tm^2 + \epsilon}\right\|_1 + \lambda_s \left\|\sqrt{\nabla_xm^2 + \nabla_ym^2 + \epsilon}\right\|_1,$$

where $$$m$$$ represents multi-slice images to be reconstructed, $$$d$$$ is gridded Cartesian k-space, $$$\lambda_{t,s}$$$are constraint parameters, $$$\nabla_{t,x,y}$$$ are temporal and spatial gradient operators and $$$\epsilon$$$ is a small value used to avoid singularity. A 3-slice SMS GROG reconstruction pipeline is shown in Figure 2.

Toeplitz method

Another approach to avoiding going from Cartesian to non-Cartesian samples at every iteration has attracted increasing interest recently^4,7. This Toeplitz method uses a Kaiser-Bessel kernel to grid the non-Cartesian data only once before starting the reconstruction iterations, and convolves the image with a 2-times oversampled point spread function to maintain reconstruction accuracy within the image size during iterations. The Toeplitz implementation for SMS data shares the same dephasing and data recombination steps stated above.

Simulation

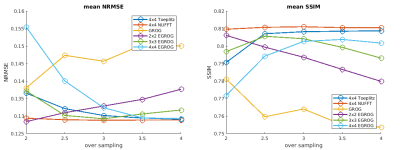
SMS radial k-space with 36 spokes per frame and 288 readouts per spoke was simulated from 3 slices single band cardiac perfusion images with 30 frames and matrix size 144x144, then reconstructed using GROG, EGROG, Toeplitz and NUFFT at oversampling 2, 2.5, 3, 3.5 and 4. The work here considers the oversampling factor as size used in Fourier transforms divided by the matrix size prescribed (so the lowest oversampling factor used here is 2, to match the 2x oversampling of the k-space acquisition). Comparisons were done using NRMSE and SSIM.

In-vivo tests

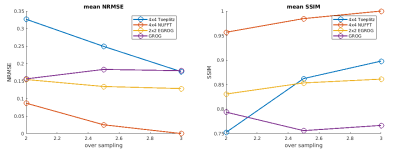
We reconstructed 12 DCE cardiac perfusion datasets of different acquisition strategies using the GROG, EGROG, Toeplitz and NUFFT at oversampling of 2, 2.5 and 3, with 6 hybrid acquisitions² and 6 multi-set SMS acquisitions¹. Then all reconstructed images were compared with NUFFT reconstruction at an oversampling of 3. NRMSE and SSIM were calculated to compare the methods.

Result and Discussion

Simulation and in-vivo test results are shown in Figure 3 and Figure 4 respectively. The NUFFT method shows consistently the best reconstruction accuracy at all oversampling factors. At oversampling of 2, the EGROG with kernel size 2x2 outperforms Toeplitz and GROG methods. All pre-interpolation methods share similar reconstruction speed, which is ~2 times faster than NUFFT.

From simulation we found that as oversampling factor increases, different kernel sizes should be used for EGROG to maintain reconstruction accuracy. This is because the shift distances decrease as grid gets finer if keeping kernel size the same, thus using small kernel at high oversample leaves acquired data less exploited. The work here only considered EGROG having a square kernel and only 2x2 kernel was used in in-vivo tests, since the focus here was on demonstrating EGROG can provide improved Cartesian k-space estimation and implementing EGROG and Toeplitz for SMS data. Further studies could explore optimizing kernels for EGROG. Applying and comparing EGROG or Toeplitz on other type of datasets other than radial SMS was not discussed here, but could also be of practical interests.

Acknowledgements

References

[1] G. Adluru, J. Mendes, Y. Tian, B. Wilson, E. DiBella. Ungated myocardial perfusion imaging with complete left ventricular coverage using radial simultaneous multi-slice imaging. ISMRM 2017.

[2] E. DiBella, D. Likhite, G. Adluru, C. Welsh, B. Wilson. A new hybrid approach for quantitative multi-slice myocardial DCE perfusion. ISMRM 2016.

[3] Tian Y, Erb KC, Adluru G, Likhite D, Pedgaonkar A, Blatt M, Kamesh Iyer S, Roberts J, DiBella E. Technical Note: Evaluation of pre-reconstruction interpolation methods for iterative reconstruction of radial k-space data. 2017;44(8):4025-4034.

[4] Corey A. Baron, Nicholas Dwork, John M. Pauly, Dwight G. Nishimura. Rapid compressed sensing reconstruction of 3D non-Cartesian MRI. MRM, 2017.

[5] Seiberlich N, Breuer F, Blaimer M, Jakob P, Griswold M. Self-calibrating GRAPPA operator gridding for radial and spiral trajectories. MRM. 2008;59(4):930-5.

[6] H. Wang, G. Adluru, L. Chen, E. G. Kholmovski, N. K. Bangerter, E. V. DiBella. Radial simultaneous multi-slice CAIPI for ungated myocardial perfusion. Magn Reson Imaging. 2016;34:1329-1336

[7] Wajer F, Pruessmann KP. Major speedup of reconstruction for sensitivity encoding with arbitrary trajectories. In Proceedings of the 9th Annual Meeting of ISMRM, Glasgow, Scotland, UK.