2904
High-Resolution T1 Mapping using Parameter-Free Low Rank Denoising1Electrical and Computer Engineering, University of Minnesota, Minneapolis, MN, United States, 2Center for Magnetic Resonance Research, University of Minnesota, Minneapolis, MN, United States, 3Computer Assisted Clincial Medicine, Heidelberg University, Mannheim, MA, Germany, 4Department of Cardiology, University of Minnesota, Minneapolis, MN, United States
Synopsis
Myocardial T1 mapping has become increasingly established for tissue characterization in numerous cardiomyopathies. However, the commonly used end-diastolic single-shot imaging imposes restrictions on the spatio-temporal resolution. In this work, we explored increased parallel imaging accelerations and higher resolutions, in conjunction with an image denoising technique that exploits inter-dependencies between the multiple images using random matrix theory. Following parallel imaging reconstruction, common noise characteristics across the images are extracted from the singular value decomposition of a Gaussian random matrix and denoised using locally low-rank regularization. Application of this technique to SAPPHIRE T1 mapping shows no corruption of the T1 time and enables parallel imaging acceleration up to 4 with an in-plane resolution of 1.1x1.1mm2 at clinical image quality.
Introduction
Myocardial T1 mapping is commonly performed based on a series of diastolic snap-shot images acquired with differential contrast weighting. However, due to the brevity of a diastolic quiescence, the in-plane resolution is limited. This gives rise to partial-volume effects which impair inter- and intra-observer variability1.
There are a number of properties shared across the multiple T1-weighted baseline images. These include common anatomical features across the weights, as well as similarities in the reconstructed noise distribution after parallel imaging. In this study we sought to exploit these similarities in a parameter-free noise reduction scheme in order to enable high resolution T1 mapping in a single breath-hold.
Methods
SAPPHIRE T1 maps were acquired with the following imaging parameters: Field strength=3T, TR/TE/FA=2.6/1.1-1.2ms/35°, FOV=300x300mm2, slice thickness=8mm, acq. window=230ms, #images=11. Spatio-temporal resolution was varied by adopting the parallel imaging factor2: R=3 (1.3x1.3mm2),R=4 (1.1x1.1mm2), R=5 (1.1x1.1mm2, acq. window=200ms, slice thickness=6.5mm).
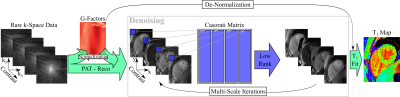
The post-processing for denoising is depicted in Figure 1. Parallel image reconstruction was performed in SNR Units3. The non-uniform noise distribution in these images was compensated for via division by the g-factor maps, leading to a uniform Gaussian noise distribution across all normalized images. Furthermore, since these multiple images share similar features locally, we hypothesized that a Casorati matrix formed by rearranging the local patches across different contrast weightings was low-rank. This property was enforced by singular value thresholding (SVT). Since all images in this series have uniform Gaussian noise, the noise part of the Casorati matrix is a random Gaussian matrix, whose entries are independent identically distributed standard normal Gaussians. Thus, the threshold was analytically derived from the singular values of a random Gaussian matrix, which follow the Marchenko-Pastur distribution4. After thresholding, images were re-normalized by the g-factor maps, resulting in the denoised images with the desired contrast in SNR units. T1 map reconstruction was performed on the denoised baseline images, using a conventional three parameter fit.
Images were acquired in three healthy subjects (33±10 y/o, 3 males), and average T1 times and T1 time variability was assessed in manually drawn septal ROIs.
Results
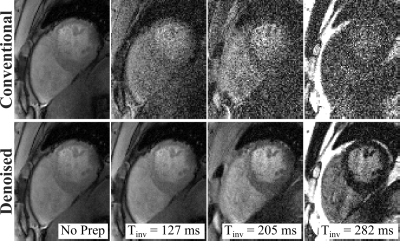
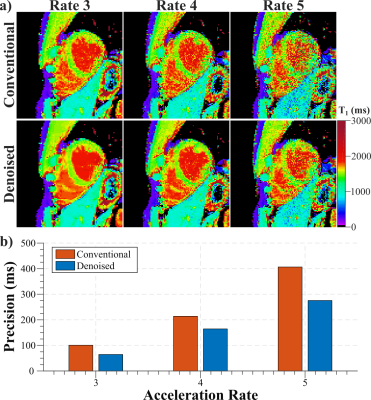
Example baseline images at acceleration rate R=4 depict readily visible noise reduction with no apparent blurring of cardiac structures using the denoising technique (Fig. 2). Visually improved homogeneity of the T1 times in the myocardium is observed while a sharp myocardial-blood interface is maintained. T1 maps at multiple acceleration rates (Fig. 3) show increased noise contamination, leading to corrupted average T1 times and highly elevated variability if no denoising is performed (Across subjects T1 time±precision: R3/R4/R5 = 1539±101/1496±214/1491±407ms). Denoising achieves consistent T1 times across all tested acceleration rates, which are in close agreement with the average T1 time obtained with low-resolution T1 mapping. Furthermore, it successfully improves in-vivo precision, leading to a 23-36% decrease in spatial variability (T1 time±precision: R3/R4/R5 = 1553±64/1526±164/1520±276ms).Discussion
Image denoising is commonly based on features within the image, often requiring a trade-off between noise reduction and retention of image details. Quantitative MRI, however, offers the advantage of acquiring multiple images with varying contrast, providing a certain degree of redundancy. This interdependency has been previously explored to allow highly accelerated image acquisition with a compressed sensing reconstruction from under-sampled data5,6,7. However, these methods commonly necessitate a random or non-Cartesian acquisition and a computationally expensive iteration between data consistency and regularization. The approach explored in this study differs from these, as it is performed in a single-step procedure following conventional parallel image reconstruction. As such, it is easily integrable in existing post-processing pipelines, with no changes in the acquisition pattern.
Analytic description of the standard normally distributed noise in the Casorati matrix enables a judicious choice of the thresholding parameter without heuristics. This was previously explored in magnitude images for diffusion MRI in the brain8, and in dynamic T1 mapping with a large number of baseline images (>50), which has more favorable low-rank properties9. With this characterization, the algorithm parameters need not be tuned for different patients, promising robust performance across a wide scale of acquisitions. This automated analytic nature of the denoising algorithm may facilitate the integration in clinical scan-protocols.
Conclusion
Parameter-free low-rank denoising enables accurate myocardial T1 mapping with visually high image quality at in-plane resolutions up to 1.1x1.1mm2 in a single breath-hold.Acknowledgements
Grant support: NIH R00HL111410, NIH P41EB015894, NIH U01EB025144 and NSF CCF-1651825.References
- Cameron D, Vassiliou VS, Higgins DM, Gatehouse PD. Towards accurate and precise T 1 and extracellular volume mapping in the myocardium: a guide to current pitfalls and their solutions. MAGMA. 2017; doi: 10.1007/s10334-017-0631-2
- Griswold MA, Jakob PM, Heidemann RM, et al. Generalized autocalibrating partially parallel acquisitions (GRAPPA). Magn Reson Med 2002;47(6):1202-10
- Kellman P, McVeigh ER. Image reconstruction in SNR units: a general method for SNR measurement. Magn Reson Med. 2005;54(6):1439-47
- Marčenko VA, Pastur LA. Distribution of eigenvalues for some sets of random matrices. Mat. Sb. N.S. 1967; 72 (114:4):507–36
- Doneva M, Börnert P, Eggers H, et al. Compressed sensing reconstruction for magnetic resonance parameter mapping. Magn Reson Med. 2010;64(4):1114-20
- Tran-Gia J, Wech T, Bley T, Köstler H. Model-based acceleration of look-locker T1 mapping. PLoS One. 2015; 10(4):e0122611
- Zhang T, Pauly JM, Levesque IR. Accelerating Parameter Mapping with a Locally Low Rank Constraint. Magn Reson Med. 2015;73(2): 655-661
- Veraart J, Fieremans E, Novikov DS. Diffusion MRI noise mapping using random matrix theory. Magn Reson Med. 2016 Nov;76(5):1582-1593
- Moeller S, Weingartner S, Akcakaya M. Multi-scale locally low-rank noise reduction for high-resolution dynamic quantitative cardiac MRI. Conf Proc IEEE Eng Med Biol Soc. 2017 Jul;2017:1473-1476
Figures