2893
Fast Dictionary-free Reconstruction in MR Fingerprinting1Department for Physics of Molecular Imaging Systems, RWTH Aachen University, Aachen, Germany, 2Multiphysics and Optics, Philips Research Europe, Eindhoven, Netherlands, 3Oncology Solutions, Philips Research Europe, Eindhoven, Netherlands
Synopsis
MR fingerprinting offers a rapid way to accurately map multiple tissue parameters. The dictionary based reconstruction under the influence of Gaussian noise is identified as a convex optimization problem and solved by a Nelder-Mead simplex algorithm. Instead of a lengthy and uniform sampling proposed by dictionay matching, the new approach using a heuristic and incoherent sampling in the $$$T_1$$$-$$$T_2$$$ space. More robust $$$T_1$$$ estimations are obtained even under severe noise environments. Thus, a robust and fast MR fingerprinting reconstruction can be made without any dictionary.
Purpose
MR fingerprinting (MRF) offers a rapid way to simultaneously map multiple tissue parameters. By varying acquisition parameters, e.g., FA and TR, along the time axis, distinguishable tissue specific signals, i.e., fingerprints, are obtained. Experimental acquired fingerprints are further compared with a Bloch simulated dictionary to identify the underlying tissue parameters, e.g., $$$T_1$$$, $$$T_2$$$, and proton density $$$\rho$$$ [1]. However, the dictionary calculation is a heavy computational burden for accurate tissue parameter mapping. In this work, a fast dictionary-free reconstruction using a Nelder-Mead simplex algorithm [3] is implemented. The noise influence on the dictionary-based matching is also investigated and a comparison between dictionary matching and the dictionary-free reconstruction is made for different signal to noise ratio (SNR) scenarios.Method
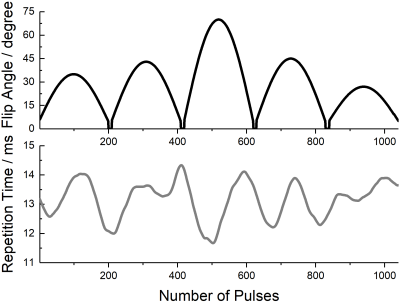
A voxel uniformly filled with a single kind of tissue was examined throughout this study. The tissue was modeled by two relaxation times ($$$T_1$$$ = 167.87 ms and $$$T_2$$$ = 104.49 ms). The noise-free fingerprint for flip angles and repetition times as depicted in figure 1 was obtained by an extended phase graph (EPG) algorithm [4]. Moreover, different SNR circumstances were simulated by adding Gaussian distributed noise onto both real and imaginary parts of the noise-free signal [2]. For each SNR value, the dot product of the signal with all dictionary entries was calculated and represented by a correlation map. The dictionary-free reconstruction algorithm aims to locate the global maximum of the dot-product array without computing the entire array, i.e., dictionary. In the initial step, a trial solution based on a priori knowledge is used to deduce two other solutions and further forming the initial simplex. The worst solution detected by calculating dot-products between trial solution signals and the target signal is replaced by a set of simplex transformation in each step. This process is repeated until the size of the simplex becomes adequately small. The optimal solution is thus the vertex holding the largest dot-product in the finial simplex. For comparison, an MRF dictionary ($$$T_1$$$ range: [10 ms, 500 ms], $$$\Delta T_1$$$ = 2 ms; $$$T_2$$$ range: [10 ms, 200 ms], $$$\Delta T_2$$$ = 2 ms) is constructed. Furthermore, the deviation of a matched $$$T_{1/2}$$$ from the nominal value was quantified by the average estimation error $$$\delta_{T_{1/2}}$$$ defined by:
$$\delta_{T_{1/2}} = \frac{1}{M}\left(\sum_{i}^{M}\frac{\left | \delta_{T_{1/2}}^{i} \right |}{T_{1/2}}\right); \delta_{T_{1/2}}^{i} = T_{1/2}^{Defined} - T_{1/2}^{Estimated}$$
Adding noise and subsequent matching was repeated M=8 times to obtain an average error. Besides, a total estimation error $$$\delta = \delta_{T_1} + \delta_{T_2}$$$ was defined to characterize the robustness of different reconstruction routines under different SNR. A gelatin phantom was measured on a 3T MRI scanner (Achieva 3T, Philips, The Netherlands). 20 constant density spiral interleaves were combined to sample the K-space. Sparse ($$$\Delta T_1$$$ = 50 ms, $$$\Delta T_2$$$ = 50 ms) and dense ($$$\Delta T_1$$$ = 5 ms, $$$\Delta T_2$$$ = 3 ms) dictionaries ($$$T_1$$$ range: [10 ms, 2500 ms], $$$T_2$$$ range: [10 ms, 600 ms]) were used for measurement image reconstruction and compared to the simplex method.
Results and discussion
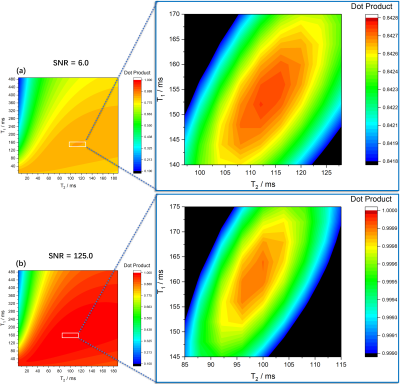
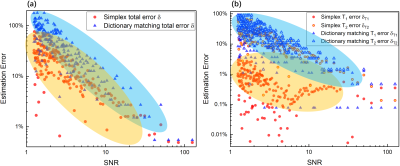
The correlation map corresponding to a dictionary-based matching process is shown in figure 2. A distinct maximum peak is found both for high and low SNR (SNR = 125.0 and 6.0) cases. Gaussian distributed noise flattens and lowers the single maximum peak without distorting the correlation surface to further induce local maximum peaks (figure 2 (a)). In contrast to a uniform sampling in the $$$T_1$$$-$$$T_2$$$ plane during conventional dictionary matching, the simplex algorithm performs an incoherent sampling. As can be seen in table 1, the iteration number for convergence of the algorithm is relatively low and strongly related to the starting values. Under high SNR (figure 3 (a)), the algorithm shows lower errors whereas the error in dictionary matching is always a trade-off between the dictionary size and the dictionary generating time (table 2). Furthermore, an increasing significant error increase dominated by the $$$T_2$$$ error (blue area in figure 3 (b)) is both observed in the simplex algorithm and dictionary matching. Nonetheless, a superior performance, comparably lower errors (orange area in figure 3 (a)) are obtained for the simplex method, allowing for robust estimation of $$$T_1$$$ even under severe noise (orange area in figure 3 (b)). In addition, a considerable computational time reduction without a sacrifice of accuracy is observed in the phantom measurement (table 2).Conclusion and Outlook
A fast dictionary-free reconstruction of MRF based on a simplex algorithm is proposed and tested via simulations and measurements. In order to boost the performance of the algorithm, parallel implementations and sliding window denoising will be added in the future.Acknowledgements
This project has received funding from the European Union's Horizon 2020 research and innovation programme under grant agreement No 667211.References
[1] Ma D, Gulani V, Seiberlich N, et al. Magnetic resonance fingerprinting. Nature. 2013; 495(7440): 187-192.
[2] Sommer K, Amthor T, Doneva M, Towards predicting the encoding capability of MR fingerprinting sequences. Magnetic Resonance Imaging. 2017; 41: 7-14.
[3] Nelder J.A, Mead R, A simplex method for function minimization. The computer journal. 1965; 7(4): 308-313.
[4] Weigel M, Extended phase graphs: dephasing, RF pulses, and echoes‐pure and simple. Journal of Magnetic Resonance Imaging. 2015; 41(2): 266-295.
[5] Jiang Y, Ma D, Seiberlich N, et al. MR fingerprinting using fast imaging with steady state precession (FISP) with spiral readout. Magnetic resonance in medicine. 2015; 74(6): 1621-1631.
Figures