2892
In vivo parametric mapping using piecewise constant flip angle and multi shot EPI MR Fingerprinting1Centre for Clinical Brain Sciences, University of Edinburgh, Edinburgh, United Kingdom, 2School of Engineering, Institute for Digital Communications, University of Edinburgh, Edinburgh, United Kingdom
Synopsis
Previous MR fingerprinting studies have used smooth variations in TR and flip angles. In this study we introduce a piecewise constant flip angle train into a standard gradient echo multi shot EPI sequence. The resulting T1, T2 and proton density maps were obtained from a phantom and healthy volunteers using only 3 distinct flip angle values (obtained by optimization over 8 different flip angles) and using iterative reconstruction. The method generates steady states covering full k-space, producing alias-free maps.
Introduction
Usually Magnetic Resonance Fingerprinting (MRF) sequences are based on pseudo-randomness in the TR and flip angles (FA) with smoothly varying changes1,2, hence driven primarily by the steady state3 responses. This motivated us to consider a piecewise constant (PC) FA structure that could similarly capture the necessary diversity in steady state responses in order to sense the parametric maps. We introduced a GRE multi-shot EPI sequence with a set of optimized PC FAs, using short and fixed TR, TE and fully sampled k-space. The parametric maps are subsequently generated using the BLIP technique4. The PC FAs allow us to simplify the optimization of the FAs by ignoring the transient dependencies and focusing on the steady state responses. This also avoiding aliasing issues and allowing us to explore links with traditional Q-MRI methods5,6. In this work the optimization across 8 PC FAs resulted in only 3 distinct FA values to produce the corresponding T1, T2 and proton density (PD) maps, indicating a similarity to DESPOT5,6.Methods
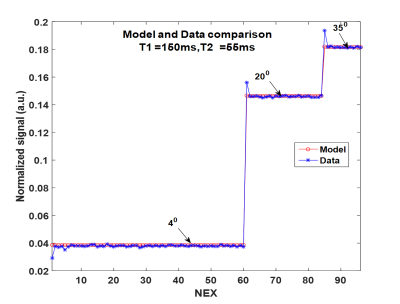
All experiments were conducted on a 1.5T HDT GE Signa MRI scanner using an 8-channel head coil. GRE EPI with a multi-shot readout sequence was modified to acquire each individual shot at a specific FA. Data were acquired from two healthy volunteers and a phantom with multiple tubes. The scanning parameters were: axial orientation, 128×128 matrix, FOV 256 mm, slice thickness 4 mm, 16-shots, BW 125 kHz, TR/TE = 33/12ms and 96 repetitions(NEX). The signal behaviour was modelled using the extended phase graph (EPG) formalism7. Each of the FAs was maintained for 12 repetitions to make it PC. Previously FA optimization using a spoiled gradient echo sequence has been performed for T1 estimation6 alone. In this work, similar to that of Cohen8, we optimize the FAs to minimize the mutual coherence between the atoms of the EPG dictionary:$$$\alpha^\star=\begin{array}{c}argmin\\ \alpha\end{array}\begin{array}{c}max\\ i\neq j\end{array}W_{i,j}\mid\langle D(T^{i},\alpha), D(T^{j},\alpha)\rangle\mid$$$ where $$$D(T^{i},\alpha)$$$ denotes the normalized dictionary atom corresponding to the parameter $$$T^{i}=\left\{T_1^i,T_2^i \right\}$$$ and the set of FAs $$$\alpha$$$. Since PC FAs cover the full k-space and hence incur no aliasing, the correlation between atoms directly measures the parameter sensitivity: a smaller mutual coherence implies better separation between the EPG responses of different parameters and thus, brings more sensitivity. Since we only consider steady state responses, an additional advantage of PC FAs is that the mutual coherence measure decouples across the FAs making FA optimization easier. In our current experiment we set $$$W_{i,j}=1$$$, and optimized over 8 PC FAs, each limited to 0-350. The optimal FAs were [40,40,40,40,40,40,200,350] resulting in only 3 distinct values, similar to Lewis6. Here the repetition of the angle 40 can be explained as boosting the discriminative power of the smallest FA where low signal levels are observed.
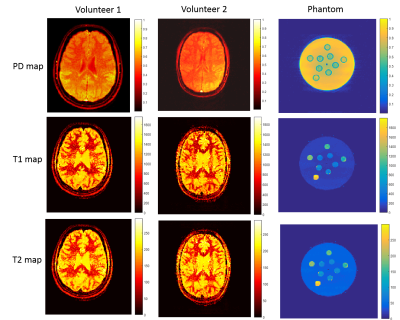
Based on observation (Figure 1b), the first 4 repetitions for each FA excitation were considered as the transient state and hence discarded and the remaining sequential shots were used as steady state to create the corresponding maps. A Dictionary was created based on the EPG model of the sequence for a wide range of $$$ T1 = 60:3:8000ms$$$ and $$$T2 = 30:0.5:2000ms$$$. The parametric maps were created by the BLIP4 algorithm, matching to the dictionary.
Conventional T1 images were acquired using SE and FSE IR and T2 images were acquired using GRE for volunteers and phantom respectively.
Results
Figure 1a shows the T1, T2 and PD maps of the volunteers and phantom generated from the proposed method. The comparisons of T1 and T2 values of the phantom with the reference maps are shown in the Figure 2.Discussion
In vivo and phantom artefact free parametric maps were produced using MRF with PC FAs and multi-shot EPI, and represents a link between traditional Q-MR5,6 and MRF. In this work the GRE multi-shot EPI scanning parameters are similar to the standard scanner set-up, e.g. using spectrally selective RF pulses and without applying an IR pulse at the beginning as used by other MRF work9,2. The feature of PC FA simplifies the FA selection since we are essentially collecting fully sampled steady state data and hence removes the need for any randomness argument (that is usually motivated from the undersampling in compressed sensing). Interestingly, the optimization resulted in only three distinct FA values to produce the parametric maps of T1, T2 and PD6. Since this method considers only the steady state behaviour, ordering of the FAs is irrelevant. Work in progress aims to consider the B1 inhomogeneity effects which would further improve sensitivity.Conclusion
A method for MRF applications has been introduced with a GRE multi-shot EPI sequence with optimized FAs. This can be implemented using only 3 distinct FA values to create parametric maps.Acknowledgements
EPSRC Compressed Quantitative MRI grant: EP/M019802/1. Scanning was carried out on a GE 1.5T scanner operating within the Edinburgh Imaging (Western General Hospital) facility, University of Edinburgh.References
1. Ma D, Gulani V, Seiberlich N, Liu K, Sunshine JL, Duerk JL, Griswold MA. Magnetic resonance fingerprinting. Nature 2013;495(7440):187-192. 2. Jiang Y, Ma D, Seiberlich N, Gulani V, Griswold MA. MR fingerprinting using fast imaging with steady state precession (FISP) with spiral readout. Magn Reson Med 2015;74(6):1621-1631. 3. Assländer J, Glaser SJ, Hennig J. Pseudo Steady‐State Free Precession for MR‐Fingerprinting. Magn Reson Med 2017;77(3):1151-1161. 4. Davies M, Puy G, Vandergheynst P, Wiaux Y. A Compressed Sensing Framework for Magnetic Resonance Fingerprinting. SIAM Journal on Imaging Sciences 2014;7(4):2623-2656. 5. Deoni SC, Rutt BK, Peters TM. Rapid combined T1 and T2 mapping using gradient recalled acquisition in the steady state. Magn Reson Med 2003;49(3):515-526. 6. Lewis CM, Hurley SA, Meyerand ME, Koay CG. Data‐driven optimized flip angle selection for T1 estimation from spoiled gradient echo acquisitions. Magn Reson Med 2015;76(3):792–802. 7. Weigel M. Extended phase graphs: Dephasing, RF pulses, and echoes - pure and simple. JMRI 2015;41(2):266-295. 8. Cohen O. In vivo optimized fast MR Fingerprinting in the Human Brain. 2016; Proc. Intl. Soc. Mag. Reson. Med, Singapore. 9. Rieger B, Zimmer F, Zapp J, Weingärtner S, Schad LR. Magnetic resonance fingerprinting using echo‐planar imaging: Joint quantification of T1 and T2∗ relaxation times. Magn Reson Med 2016;78(5):1724–1733.Figures