Introduction

Magnetic Resonance Fingerprinting¹ (MRF) can provide fast and quantitative measurements of several clinically-relevant tissue properties using a pulse sequence with pseudo-random acquisition parameters. However, T₁, T₂ values estimated from MRF rely on an accurate model of the signal dynamics, in order to derive tissue properties by matching the acquired signal with a “dictionary” of pre-calculated signal evolutions. The reported T₁, T₂ values derived from MRF are not yet perfectly robust in some situations. A likely cause for deviation of the estimated relaxation values from their true values is that MRF dictionaries have in general not included apparent diffusion coefficients (ADC), primarily due to the difficulties associated with simulating the MRF signal evolutions. Hence, the purpose of this work was to analyze the errors induced by omitting diffusion in estimates of relaxation parameters derived from the MRF- Fast Imaging with Steady Precession (FISP) sequence², by including a diffusion propagator in Bloch equation simulations.

Methods

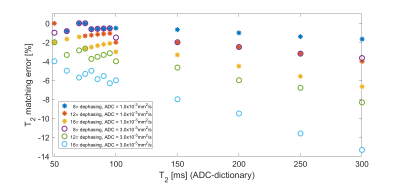
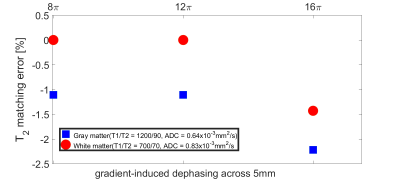
Bloch simulations with a diffusion propagator were applied to the MRF-FISP sequence (Fig.1). In this study, three sizes of the gradient-induced dephasing (8, 12, 16$$$\pi$$$) across the slice thickness (5mm) were employed during a 1ms magnetic field gradient in each repetition time (TR). TR and flip angles (FA) were varied throughout the acquisition as shown in Fig.1. Firstly, “no-ADC-dictionary” MRF signal evolutions were generated over a range of T₁ (100-3000ms, in 1ms increments), T₂ (20-300ms, in 1ms increments) using the conventional Bloch simulations. For the purpose of analyzing the matching errors between signal evolutions with and without diffusion, MRF signal evolutions corresponding to three “ADC-dictionaries”, including two ADC values (1.0$$$\times$$$10^-3 and 3.0$$$\times$$$10^-3mm²/s) were generated for the three dephasing sizes. For each of the ADC-dictionaries, the following T₁ and T₂ values were employed: fixed T₁=800ms with a range of T₂=50-300ms, and T₁=500-3000ms with fixed T₂=80ms. In addition, to evaluate the matching errors in tissue properties, signal evolutions for grey matter (GM) and white matter (WM) were also generated: T₁/T₂=1200/90ms, ADC=0.64$$$\times$$$10^-3mm²/s, and T₁/T₂=700/70ms, ADC=0.83$$$\times$$$10^-3mm²/s for GM and WM, respectively³. Off-resonance frequencies were set to be equal to zero in all cases. Each ADC-dictionary entry was matched with an entry of the no-ADC-dictionary by employing a template-matching algorithm¹. T₁ and T₂ matching percentage errors³ between the no-ADC-dictionary and the ADC-dictionary entries were calculated for each of the three different dephasing sizes: $$$Error=\frac{T_{1,2}(no-ADC-dictionary)-T_{1,2}(ADC-dictionary)}{T_{1,2}(ADC-dictionary)}\times100$$$[%].

Results

Figs.2 and 3 show matching errors when T₂ was varied (T₁ fixed) and T₁ was varied (T₂ fixed), respectively. These results imply that for all conditions, both of the relaxation parameters were underestimated in the matching process for the MRF-FISP sequence if diffusion was not accounted for. Fig.2 shows that the size of the matching error (degree of underestimation) of T₂ increased with larger T₂ values and dephasing sizes. Conversely, Fig. 3 shows that the matching error of T₁ values was relatively smaller than T₂ matching errors, with some evidence of a trend to higher matching error for lower T₁. Over all simulations, the T₁ matching errors were always lower in magnitude than -1%, even in the case of 16$$$\pi$$$ dephasing with ADC=3.0$$$\times$$$10^-3mm²/s, whilst T₂ matching errors reached ~-10% for 16$$$\pi$$$ and long T₂. Fig. 4 shows the T₂ matching errors for GM and WM. As the dephasing size increased, the degree of T₂ underestimation increased in magnitude, reaching an error of -2.2% for GM in the case of 16$$$\pi$$$ dephasing.

Discussion

Here we presented an error analysis of T₁ and T₂ estimation of MRF-FISP sequence with different dephasing gradient moment in each repetition time. While Extended Phase Graphs (EPG)⁴ can also be employed to generate MRF dictionaries, diffusion propagator, while taking longer time in calculation, could be more flexible to take account other parameters, such as off-resonance for extending the current work. This study indicates that the previously reported MRF T₁, T₂ values are likely underestimated and should be corrected. However, the error introduced by the diffusion sensitivity is only 2.2% in normal gray matter with 16$$$\pi$$$.

Conclusion

Potential T₁, T₂ matching errors due to the omission of diffusion in the signal evolution during the MRF-FISP sequence have been evaluated by implementing a diffusion propagator in Bloch simulations. In the near future, inclusion of ADC values in MRF dictionaries should permit the use of MRF pulse sequences with magnetic field gradients of large magnitude.

Acknowledgements

This work was supported by Siemens Healthcare and NIH grants 1R01EB016728, 1R01DK098503 and 1R01BB017219.