2890
CoverBLIP: scalable iterative matched-filtering for MR Fingerprint recovery1School of Engineering, University of Edinburgh, Edinburgh, United Kingdom, 2School of Engineering and Physical Sciences, Heriot-Watt University, Edinburgh, United Kingdom
Synopsis
Current popular methods for Magnetic Resonance Fingerprint (MRF) recovery are bottlenecked by the heavy computations of a matched-filtering step due to the size and complexity of the fingerprints dictionary. In this abstract we investigate and evaluate the advantages of incorporating an accelerated and scalable Approximate Nearest Neighbour Search (ANNS) scheme based on the Cover trees structure to shortcut the computations of this step within an iterative recovery algorithm and to obtain a good compromise between the computational cost and reconstruction accuracy of the MRF problem.
Purpose
Current proposed solutions for the high dimensionality of the MRF reconstruction problem1 rely on a linear compression step to reduce the matching computations2,3 and boost the efficiency of fast but non-scalable searching schemes such as the KD-trees4. However such methodologies often introduce an unfavourable compromise in the estimation accuracy when applied to nonlinear data structures such as the manifold of Bloch responses with possible increased dynamic complexity and growth in data population5.
To address this shortcoming we propose an inexact iterative reconstruction method, dubbed as the Cover BLoch response Iterative Projection (CoverBLIP). Iterative methods improve the accuracy of their non-iterative counterparts6 and are additionally robust against certain accelerated approximate updates, without compromising their final accuracy7,8. Leveraging on these results, we accelerate matched-filtering using an ANNS algorithm based on Cover trees9 with a robustness feature against the curse of dimensionality.
Algorithm
The CoverBLIP iterations consist of $$X^{t+1}=\widetilde{\mathcal{P}}_D\left( X^t - \mu A^H\left(A(X^t)-Y\right)\right),$$ where, $$$Y\in\mathbb{C}^{m\times L}$$$ is the undersampled k-space measurements across $$$L$$$ temporal frames, $$$\mu$$$ is the step-size (with line-search6), $$$X\in\mathbb{C}^{n \times L}$$$ is the spatio-temporal images reconstructed at iteration $$$t$$$, and $$$D\in\mathbb{C}^{d \times L}$$$ denotes the dictionary of $$$d\gg L$$$ fingerprints. The forward-adjoint operators $$$A,A^H$$$ correspond to the gradient updates and model the multi-coil sensitivities and the per-frame subsampled 2D Fourier Transforms. $$$\widetilde{\mathcal{P}}_D(.)$$$ is the approximate matched-filtering similar to4,6 consisting of i) a search over the normalized dictionary to replace temporal pixels of $$$X^{t+1}$$$ with their (approximate) nearest fingerprints, and ii) a proton density rescaling. For the search step we however use Cover trees’ fast $$$(1+\epsilon)$$$-ANNS algorithm with controlled approximation levels $$$\epsilon\geq0$$$8,9. For smooth $$$O(1)$$$-dimensional manifold data, Cover tree’s complexities namely the storage, (offline) construction and ANNS times scale as $$$O(d), O(d\log(d))$$$ and $$$O(\epsilon^{-1}\log(d))$$$, respectively9,10. Remarkably the search complexity grows logarithmically with dataset population as compared to the linear complexity of a brute-force search used in6.
When applicable and with a compromise in the accuracy, a temporal compression similar to4 can be optionally used to further shrink dimensions of $$$X^t, D$$$ across the $$$k$$$ dominant Eigen-components of $$$DD^H$$$. This also includes a compromise between cheaper distance evaluations during the search steps and the additional cost of iterative compression-basis applications (particularly when $$$k$$$ has to be large and the gradient updates are using cheap FFT operations e.g. in Cartesian sampling).
Methods
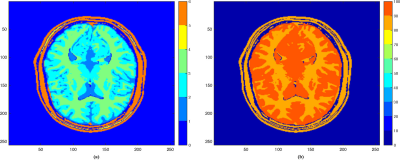
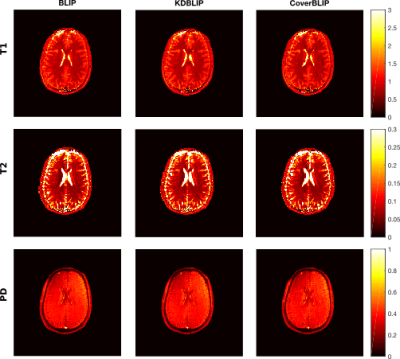
Methods are tested on a numerical brain phantom11, a physical tube phantom and a healthy human brain (scanner data collected with a 12-channel head coil 3T GE MR750w scanner, GE Medical Systems, Milwaukee, WI). Sampling follows the multi-shot EPI-MRF protocol6 (in contrast with the existing single-shot EPI-MRF approaches12,13) with k-space compression factors x32 and x16 for the numerical and scanner data, respectively. The Numerical phantom is synthesized (256x256 sized T1, T2 maps in Figure 1 and off-resonance B0=0) using an Inversion Recovery (IR) Balanced SSFP sequence with L=1000 Flip Angles (FA), TR and TE similar to3. The constructed dictionary consists of 321’640 fingerprints for combinations of T1=[100:40:2000,2200:200:6000], T2 = [20:2:100,104:4:200,220:20:600], B0=[-250:40:-190,-50:2:50,190:40:250]. The scanner data uses IR Quantitative Transient-state Imaging (QTI) sequence (TR=16 ms, Tinv = 18 ms, 22:5x22:5 cm FOV, 128x128 matrix size, 1.3 mm in-plane resolution and 5 mm slice thickness) with a linear ramp FA variation 1°-70° across L=500 frames14. Dictionary construction here uses the EPG model15 with 23’866 fingerprints for combined T1=[10:20:1900,2100:100:6000], T2=[20:1:120,122:2:200,210:10:600], where T1>T2.Results and discussion
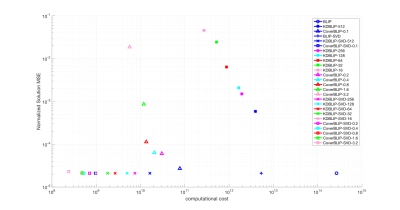
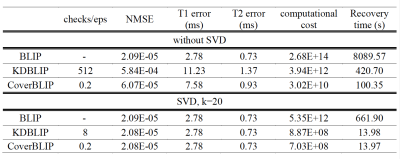
We compare the reconstruction times and accuracies of three iterative methods: BLIP6 with exact NNS using MATLAB’s matrix product, KDBLIP with randomize KD-trees ANNS (approximations controlled by the number of Checks) using the FLANN package16, and CoverBLIP using Cover trees’ $$$(1+\epsilon)$$$-ANNS with a parallel MATLAB interface to17. Experiments are conducted on a desktop with 8 CPU-Cores and 64GB RAM.
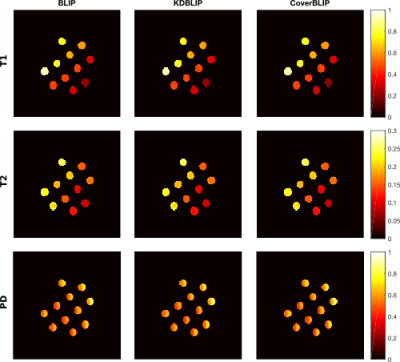
Cover tree construction takes around 10 and 0.8 seconds for the IR-BSSFP and EPG full-size dictionaries. Results tested on the numerical phantom (Figures 2 and 3) show that in the full-size ambient dimension CoverBLIP significantly outperforms the two other methods: better time-accuracy than KDBLIP, and a similar accuracy to BLIP however with $$$O(10^4)$$$ cheaper operations for matched-filtering. Since the numerical phantom is low-rank, we also apply temporal compression ($$$k$$$=20) i.e. a beneficial setup for the KD-trees search: CoverBLIP and KDBLIP report comparable time-accuracies with acceleration factors x50 compared to BLIP. Results tested on the scanner data (Figures 4 and 5) show comparable recovered maps for all methods. Here the computational gain of approximate methods is less visible due to using a smaller size EPG dictionary. Nonetheless, CoverBLIP still outperforms other methods in the total runtime with matched-filtering accelerations x2 and x5-7 compared to KDBLIP and BLIP, respectively.
Acknowledgements
We thank Arnold Benjamin (Centre for Clinical Brain Sciences, University of Edinburgh) and Dr. Pedro Gomez (GE Global Research, Munich) for providing the multi-shot EPI-MRF scanner data. This work is partly funded by the EPSRC grant EP/M019802/1 and the ERC C-SENSE project (ERCADG-2015-694888).References
[1] D. Ma, V. Gulani, N. Seiberlich, K. Liu, J. Sunshine, J. Durek, and M. Griswold, “Magnetic resonance fingerprinting,” Nature, vol. 495, no. 7440, pp. 187–192, 2013.
[2] McGivney, D. F., Pierre, E., Ma, D., Jiang, Y., Saybasili, H., Gulani, V., and Griswold, M. A., “SVD compression for magnetic resonance fingerprinting in the time domain. IEEE transactions on medical imaging, 33(12), 2311-2322, 2014.
[3] Cauley, S.F., Setsompop, K., Ma, D., Jiang, Y., Ye, H., Adalsteinsson, E., Griswold, M.A. and Wald, L.L., “Fast group matching for MR fingerprinting reconstruction,” Magnetic resonance in medicine, 74(2), pp.523-528, 2015.
[4] Cline, C.C., Chen, X., Mailhe, B., Wang, Q., Pfeuffer, J., Nittka, M., Griswold, M.A., Speier, P. and Nadar, M.S., “AIR-MRF: accelerated iterative reconstruction for magnetic resonance fingerprinting,” Magnetic Resonance Imaging, 41, pp.29-40, 2017.
[5] Wang, C.Y., Coppo, S., Mehta, B.B., Seiberlich, N., Yu, X., and Griswold, M.A., “Magnetic Resonance Fingerprinting with Quadratic RF Phase for Simultaneous Measurement of δf, T1, T2, and T2*,” in Proc. Intl. Soc. Mag. Reson. Med., 2017.
[6] M. Davies, G. Puy, P. Vandergheynst, and Y. Wiaux, "A compressed sensing framework for magnetic resonance fingerprinting," SIAM Journal on Imaging Sciences, vol. 7, pp. 2623-2656, 2014.
[7] Golbabaee, M. and Davies, M.E., “Inexact Gradient Projection and Fast Data Driven Compressed Sensing,” arXiv preprint arXiv:1706.00092., 2017.
[8] Golbabaee, M., Chen, Z., Wiaux Y., and Davies M. E.,"Cover tree for fast MR fingerprint Recovery", Proceedings of the IEEE workshop on Machine Learning for Signal Processing (MLSP), 2017, arXiv:1706.07834.
[9] Beygelzimer, A., Kakade, S. and Langford, J., “Cover trees for nearest neighbor,” In Proceedings of the 23rd international conference on Machine learning, pp. 97-104, ACM, 2006.
[10] Krauthgamer, R. and Lee, J.R., “Navigating nets: simple algorithms for proximity search,” In Proceedings of the fifteenth annual ACM-SIAM symposium on Discrete algorithms, pp. 798-807. Society for Industrial and Applied Mathematics, 2004.
[11] Brainweb data repository, available at: http://brainweb.bic.mni.mcgill.ca/brainweb/
[12] Rieger, B., Zimmer, F., Zapp, J., Weingärtner, S. and Schad L.R., "Magnetic resonance fingerprinting using echo‐planar imaging: Joint quantification of T1 and T2∗ relaxation times," Magnetic resonance in medicine, vol. 78, pp. 1724–1733, 2017.
[13] Cohen, O., Sarracanie, M., Rosen, M.S. and Ackerman, J.L.,"In Vivo Optimized Fast MR Fingerprinting in the Human Brain," in Proc. Intl. Soc. Mag. Reson. Med., 2016.
[14] Gomez, P.A., Buonincontri, G., Molina-Romero, M., Sperl, J.I., Menzel, M.I., and Menze, B.H., "Accelerated parameter mapping with compressed sensing: an alternative to MR Fingerprinting," in Proc Intl. Soc. Mag. Reson. Med., 2017.
[15] Weigel, M., "Extended phase graphs: dephasing, RF pulses, and echoes‐pure and simple," Journal of Magnetic Resonance Imaging, vol. 41, pp. 266-295, 2015.
[16] Available at: http://www.cs.ubc.ca/research/flann/
[17] Available at: http://hunch.net/~jl/projects/cover_tree/cover_tree.html
Figures