Introduction:

The conventional dictionary matching approach for MR Fingerprinting (MRF) [1] has two main challenges: long computation time and huge round-off error because of the use of discrete MR-parameter space. Convolutional Neural Network (CNN) [2] has been widely used in the MR fields [3-5] thanks to its learning and generalization capability. In this work, we demonstrate that MRF reconstruction using CNN (MRF-CNN) can significantly improve the fidelity of MRF reconstruction.

Methods:

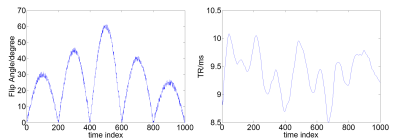
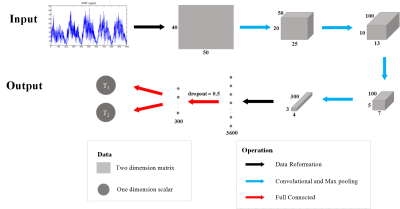
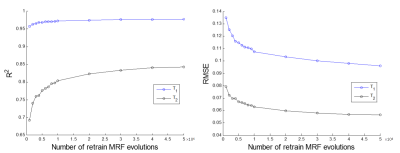
This study was based on the simulation of MRF acquired using the IR-bSSFP sequence [1] with the TR and FA train as shown in Fig. 1 and no. of dynamics = 1000 using variable density spiral and the spiral trajectory rotated 7.5° from one time point to the next. MRF dictionary was simulated with 475600 combinations of T₁ values in the range 200~2500 ms (in an increment of 20 ms), T₂ values in the range 1~500 ms (in an increment of 5 ms), and off-resonance (ΔB) values in the range -120~120 Hz (in an increment of 4 Hz within -40~40 Hz or 8 Hz beyond the range). MRF dictionary was used to train our newly proposed MRF-CNN (herein denoted as dictionary-trained MRF-CNN), and the architecture of which was illustrated in Fig. 2. The loss function is defined as: $$$\frac{1}{N}{\sum_{}\parallel y-\hat{y}\parallel_{2}}+\lambda \parallel W \parallel_{2}$$$, where $$$y$$$ represents the true T₁/T₂ and $$$\hat{y}$$$ the corresponding reconstruction values, $$$W$$$ the weighting of MRF-CNN, $$$\parallel\cdot\parallel_{2}$$$ the L₂ norm, and $$$\lambda$$$ the regularization parameter. The first term of the loss function is to quantify the accuracy of reconstruction result and the second term is the L₂-regularization to prevent overfitting. The MR signal evolutions in the continuous parameter space, generated by randomly selected T1, T2 and ΔB from the continuous-parameter space, were used to verify the reconstruction fidelity of MRF-CNN. We further explored the performance of our proposed MRF-CNN in the presence of Gaussian noise contamination. To utilize the intrinsic transfer learning capability of MRF-CNN, MR signal evolutions in the continuous parameter space with various levels of Gaussian noise were used to retrain the dictionary-trained MRF-CNN (herein denoted as retrained MRF-CNN). An additional set of MR signal evolutions in the continuous parameter space with the same level of Gaussian noise was subsequently used to test the performance of the retrained MRF-CNN. The SNR of MR signal evolutions ranged from 0 dB to 14 dB with an increment of 2 dB, and the number of MR signal evolutions for retraining was fixed at 50000 for all noise levels. The effect of the number of MR signal evolutions for retraining on MRF reconstruction fidelity of the retained MRF-CNN was also explored. The numbers of MR signal evolutions to test was given as 1000-50000 (in an increment of 1000 below 10000 and an increment of 10000 above 10000), and the SNR was fixed at 0 dB. The reconstruction fidelity of the conventional dictionary matching approach, the dictionary-trained MRF-CNN model and the-retrained MRF-CNN model were compared with the true values.

Results and Discussion:

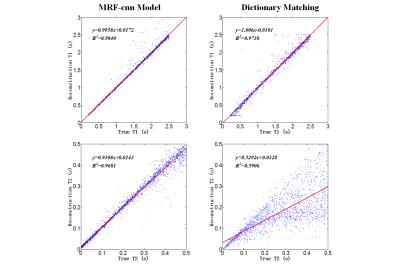
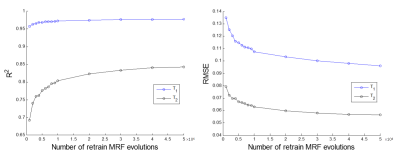
For MRF data without noise contamination, the reconstruction fidelity of dictionary-trained MRF-CNN is significantly better than that of the conventional MRF dictionary matching approach (Fig. 3) - T₁ (R² : 0.98 vs 0.97) and T₂ (R² : 0.97 vs 0.59) which means the MRF-CNN has better generalization capability than dictionary matching. In the presence of noise (SNR: 14 - 0 dB), the reconstruction fidelity of dictionary-trained MRF-CNN depends heavily on noise level - T₁ (R²: 0.98 - 0.89, RMSE: 0.09 – 0.37), T₂ (R²: 0.93 - 0.57, RMSE: 0.04 – 0.11) (Fig. 4). On the other hand, that of the retrained MRF-CNN is largely unaffected and higher than that of dictionary-trained MRF-CNN even when the power of noise and MR signal evolution is equal (Fig. 4, T₁/T₂: 0.98/0.84 (R²), 0.10/0.06 (RMSE)). As shown in Fig. 5, the number of MR signal evolutions for retraining MRF-CNN has larger impact on T₂ than T₁, and that 50000 MR signal evolutions are necessary to retrain the dictionary-trained MRF-CNN to achieve high MRF reconstruction fidelity when SNR is 0 dB.

Conclusion:

We have successfully demonstrated that the fidelity of MRF reconstruction can be significantly improved by using convolution neural network. Our study also shows that retraining of the neural network is necessary in order to achieve high MRF reconstruction fidelity in the presence of Gaussian noise.

Acknowledgements

No acknowledgement found.