Introduction

Iterative k-t SENSE (1) reconstruction relies on the fast Fourier transform (FFT) for speed. A simple strategy to reduce reconstruction time is to make the cuboid reconstruction field of view (FOV) fit tight around the imaged object, thereby reducing the size of the data array that must be transformed with the FFT. Further tailoring can be achieved using a hexagonal FOV (2). For the general case, the multidimensional fast Fourier transform (MFFT) (3,4) can be used to Fourier transform any n-dimensional periodic grid and thereby enables fast reconstruction of images with arbitrary non-cuboid voxels and FOVs (Fig. 1). We demonstrate that the reconstruction time for iterative k-t SENSE can be reduced without loss of image quality by tailoring a tight subject-specific non-cuboid FOV to the subject.

Method

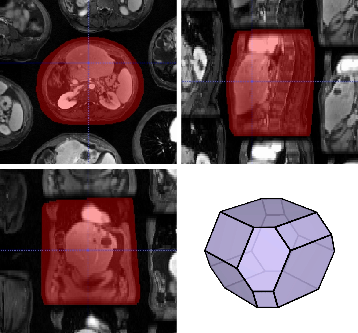
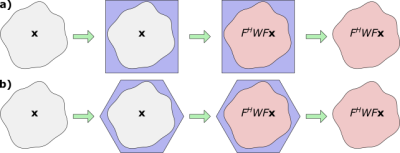
Following administration of a Gd-based contrast agent, a subject was scanned with a 3-D golden-angle stack-of-starts gradient-echo sequence (5) for 6 min as part of a pilot study of individualized adaptive radiation therapy for hepatocellular carcinoma. A 4-D image was reconstructed by solving the regularized normal equation $$$(E^HE + R)\mathbf{x} = E^H\mathbf{y}$$$ using the conjugate gradient (CG) method, where $$$\mathbf{x}$$$ are the pixel values of the 4-D image to reconstruct inside a reconstruction domain (Fig. 2), $$$\mathbf{y}$$$ are the samples collected in k-space, $$$E$$$ is the encoding matrix and $$$R$$$ is a regularizer determined from prior knowledge of the SNR in x-f space (1). The reconstruction domain was chosen as the convex hull of the subject’s external contour plus a 1-cm margin (Fig. 2). $$$E^H\mathbf{y}$$$ was calculated using NUFFTs (6–8) and estimated coil sensitivity profiles whereas $$$E^HE$$$ was rewritten as $$$\sum_iS_i^HZ^H\mathcal{F}^HW\mathcal{F}ZS_i$$$ where $$$S_i$$$ are the coil sensitivity profiles, $$$Z$$$ is a zero-filling operator that pads the reconstruction domain to the size of the MFFT FOV (Fig. 3), $$$W$$$ is the Fourier transform of the point-spread function (PSF) produced by the radial k-space sampling pattern and $$$\mathcal{F}$$$ is the Fourier transform. The non-cuboid MFFT FOV was selected in a two-step procedure. First, a tight FOV was chosen as that which most densely packed the reconstruction domain without overlap (Fig. 3). Second, this FOV was doubled to avoid PSF wrap around (9). The MFFT was implemented by diagonalizing the periodicity matrix, $$$P$$$, of the FOV into a modified Smith normal form (SNF), $$$P=UDV^T$$$, and then using conventional FFT software on the image array permuted according to the unimodal matrices $$$U$$$ and $$$V$$$ of the modified SNF. This permutation operation was merged into the zero-filling operator, $$$Z$$$, for speed. The modification of the SNF distributed the prime factors of $$$\det(P)$$$ across the diagonal elements of $$$D$$$ to produce a transform array size suitable for multithreaded FFT. CG reconstruction was stopped after 20 iterations. The 4-D pixels in the non-cuboid FOV were compared to corresponding pixels in an image reconstructed using the most densely packing cuboid FOV.

Results

Images reconstructed using cuboid and non-cuboid FOVs were identical except for round-off differences after the cuboid and non-cuboid FFTs. Non-cuboid images reconstructed in 82% of the time required for cuboid images and required 89% of the memory for each FFT.

Discussion

We have demonstrated the feasibility of using non-cuboid FOVs combined with the MFFT to speed up iterative k-t SENSE reconstruction for arbitrary k-space trajectories. While our current reconstruction uses fast convolution with a pre-calculated PSF, non-cuboid FOVs could be used for NUFFT-based reconstruction with pre-calculated convolution gridding weights (7) for additional speed. However, for NUFFT-based reconstruction, finding the optimal shape of the convolution kernel is still an unsolved problem. In this study, we used cuboid voxels to allow direct comparison to corresponding voxels in images with conventional cuboid FOVs. Additional speedup could be achieved by tailoring the voxel shape and in extension the k-space FOV to the k-space sampling domain. In this case, voxels shaped as hexagonal prisms would be optimal for a stack-of-stars sequence with its cylindrical sampling domain and could reduce reconstruction time further by about 13% (2).

Acknowledgements

This work was supported by NIH/NCI PO1 CA059827.