2869
Multi-Contrast 3D MR Image Reconstruction from Incomplete Measurements with Spatially Adaptive Priors1Department of Biomedical Engineering, Sungkyunkwan University, Suwon, Republic of Korea, 2Department of Brain and Cognitive Engineering, Korea University, Seoul, Republic of Korea
Synopsis
Magnetic resonance imaging (MRI) is well established as a clinical routine in which multiple sets of data are typically acquired to produce various image contrasts such as T1, T2, FLAIR, etc. Despite the versatile nature of MRI, multi-contrast data acquisition is highly time consuming particularly when 3D encoding is needed. To address this issue, in this work we propose a novel, multi-contrast 3D MR image reconstruction with spatially adaptive priors by exploiting sharable information across the contrast dimension: edge and coil sensitivity maps. The proposed method consists of the following three steps: 1) estimation of edge maps common over all contrasts, 2) estimation of contrast-specific edge maps, and 3) multi-contrast image reconstruction with spatially adaptive, contrast-specific edge priors. In vivo experimental studies show that the proposed method enables T1, T2, and FLAIR 3D isotropic (1mm3) imaging roughly in 5-6 minutes.
Introduction
Magnetic resonance imaging (MRI) is well established as a clinical routine in which multiple sets of data are typically acquired to produce various image contrasts such as T1, T2, FLAIR, etc. Despite the versatile nature of MRI, multi-contrast data acquisition is highly time consuming particularly when 3D encoding is needed[1]. To address this issue, in this work we propose a novel, multi-contrast 3D MR image reconstruction with spatially adaptive priors by exploiting sharable information across the contrast dimension: edge and coil sensitivity maps. The proposed method consists of the following three steps: 1) estimation of edge maps common over all contrasts, 2) estimation of contrast-specific edge maps, and 3) multi-contrast image reconstruction with spatially adaptive, contrast-specific edge priors. In vivo experimental studies show that the proposed method enables T1, T2, and FLAIR 3D isotropic (1mm3) imaging roughly in 5-6 minutes.Materials and Methods
Multi-Contrast 3D Data acquisition: Data (T1, T2, and FLAIR) were acquired in volunteers on a 3T whole-body MR scanner (uMR770, UIH, Shanghai). Imaging parameters common to all contrasts were: FOV = 240x240x176mm3, encoding matrix = 240x240x176, and the number of receiver channels = 17. Imaging parameters with T1-contrast were: TR/TE/TI= 7.2/3.1/750ms, bandwidth=250Hz/pix; those with T2-contrast were: TR/TE=2000/330ms, TEeff=142ms, bandwidth=600Hz/pix, ETL=160, ESP=4.18ms; and those with FLAIR were: TR/TE/TI =5000/461/1557ms, TEeff=154ms, bandwidth= 750Hz/pix, ETL =240, and ESP =3.72.
Multi-Contrast 3D Image Reconstruction:
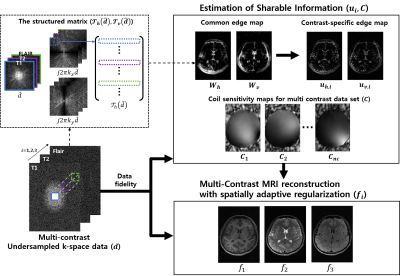
1) Estimation of edge and coil sensitivity maps common to all contrasts: MR signals in each contrast with incomplete measurements are denoted by:
$$d_i=Ef_i$$
where $$$i$$$ is the index of each contrast ($$$i$$$ = 1,2,3 for T1, T2, FLAIR, respectively), $$$d_i$$$ is the measured data in k-space, $$$f_i$$$ is the desired multi-contrast image, $$$E=CF_u$$$ is the encoding operator, $$$C$$$ is the coil sensitivity maps and $$$F_u$$$ is the undersampling Fourier operator. The common edge map ($$$W$$$) is constructed by combining the bases of null space for the structured matrix $$$\Gamma (\hat{d})$$$ in which a sliding patch of low frequency Fourier samples is row-vectorized. This approach comes from the fact that the Fourier coefficients of the partial derivatives of an image satisfy a linear, annihilating filter relation [2] by:
$$\Gamma (\hat{d})W=0$$
where $$$\hat{d}$$$ is the Fourier samples in the central region of k-space across all contrasts, $$$W=[W_v,\, W_h]$$$ and consists of vertical and horizontal edge maps common to all contrasts. Coil sensitivity maps, which are supposedly invariant, are generated from the fully sampled low-frequency k-space averaged over all contrasts.
2) Estimation of contrast-specific edge maps: The contrast-specific edge map ($$$u_i$$$) is estimated by solving the following optimization problem with the common edge priors:
$$\arg \underset{u_{v,i}}{min} \left \| \partial_{x}f_{i}-u_{v,i} \right\|_{2}^{2}+\lambda_v \left \| J(W_v)(u_{v,i}-W_v))) \right \|_{2}^{2} $$
$$\arg \underset{u_{h,i}}{min} \left \| \partial_{y}f_{i}-u_{h,i} \right\|_{2}^{2}+\lambda_h \left \| J(W_h)(u_{h,i}-W_h))) \right \|_{2}^{2} $$
where $$$\partial_{x}f_{i}$$$ and $$$\partial_{y}f_{i}$$$ represent vertical and horizontal image gradients and $$$J(W)$$$ contains the weight coefficients.
3) Image reconstruction using spatially adaptive, contrast-specific edge priors: multi-contrast images are reconstructed from incomplete measurements by solving the following optimization problem with the contrast-specific priors:
$$\arg \underset{f_{i}}{min} \left \| d_{i}-Ef_{i} \right\|_{2}^{2}+\lambda_1 \left \|u_{v,i}^{*}\partial_{x}f_{i} \right \|_{1}+\lambda_2 \left \|u_{h,i}^{*}\partial_{y}f_{i} \right \|_{1}$$
where $$$\lambda$$$ is the regularization parameter, ||∙||2 is the Euclidian norm, and ||∙||1 is the 1-norm. The entire diagram of the proposed reconstruction method is illustrated in Figure 1.
Results
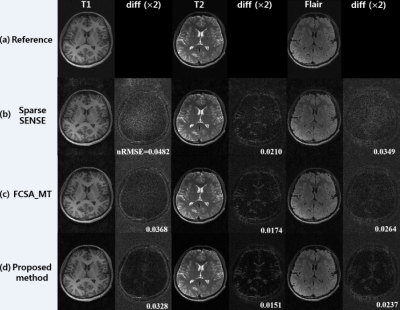
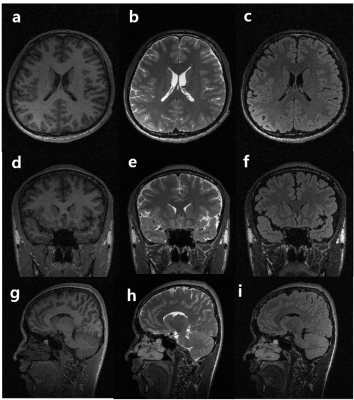
Figure 2 represents T1-, T2- and FLAIR T2-weighted images reconstructed using conventional SPARSE SENSE (b) [3], FCSA_MT (c) [4], and the proposed method (d) for comparison with a reduction factor (R) of 6. The image from the full-sampled data (a) is represented for reference. A difference image between the reference and the estimate in each contrast is presented. Even with R = 6, the proposed method exhibits relatively lower level of artifacts and noise. Fig. 3 represents T1, T2, and FLAIR 3D images (reformatted into the axial, coronal, and sagittal orientations) reconstructed using the proposed method with R = 6. It is noted that the proposed method preserves edges well without apparent artifacts and amplified noise.Discussion and Conclusion
We successfully demonstrated the feasibility of the proposed, multi-contrast 3D MRI reconstruction with spatially adaptive, contrast-specific edge priors from incomplete measurements (R = 6). It is expected that the proposed method enables T1, T2, and FLAIR 3D isotropic (1mm3) imaging roughly in 5-6 minutes and potentially replaces conventional multi-contrast imaging scenarios.Acknowledgements
We appreciate Guobin Li and Chaohong Wang at the United Imaging Healthcare for sharing multi-contrast k-space data. This research was supported by the National Research Foundation of Korea (NRF) funded by the Ministry of Science (2016M3C7A1913844, NRF-2017R1A2B4012581).References
[1] Bilgic, et al Multi-contrast Reconstruction with Bayesian Compressed Sensing. Magnetic Resonance in Medicine. 2011; 66:1601–1615.
[2] Greg, et al. Off-the-grid recovery of piecewise constant images from few Fourier samples. CoRR. 2015; abs/1510.00384
[3] Otazo, et al. Combination of Compressed Sensing and Parallel Imaging for Highly Accelerated First-Pass Cardiac Perfusion MRI. Magnetic Resonance in Medicine. 2010; 64:767–776.
[4] Junzhou Huang, et al. Fast multi-contrast MRI reconstruction. MRI. 2014; 32:1344–1352
Figures