2846

Reconstruction of quantitative proton density maps from routine clinical data
Antonio Ricciardi1,2,3, Francesco Grussu1,3, Rebecca Samson1, Daniel C Alexander3, and Claudia Angela Gandini Wheeler-Kingshott1,4,5

1Queen Square MS Centre, Department of Neuroinflammation, UCL Institute of Neurology, Faculty of Brain Sciences, University College London, London, United Kingdom, 2Department of Medical Physics and Biomedical Engineering, University College London, London, United Kingdom, 3Centre for Medical Image Computing, Department of Computer Science, University College London, London, United Kingdom, 4Department of Brain and Behavioral Sciences, University of Pavia, Pavia, Italy, 5Brain MRI 3T Research Centre, C. Mondino National Neurological Institute, Pavia, Italy

Synopsis

Quantitative proton density (qPD) mapping can be used to measure tissue water content, whose alteration are often linked to pathological conditions. Quantitative MRI methods have been developed in order to make results numerically coherent, but require specific sequences often missing in standard clinical protocols. In this study, an existing approach for the reconstruction of qPD maps from clinical data was corrected to take into account excitation B1 field inhomogeneities, and compared to qPD maps obtained via multi parametric mapping (MPM). The applied correction made clinical-derived qPD maps more similar to the MPM reference than the uncorrected method, without the need of additional specific sequences.

Introduction

Proton density (PD) measures the concentration of water protons in tissues, whose alteration can be symptomatic of disease. Multi-parametric mapping (MPM) is a comprehensive quantitative approach providing maps of quantitative PD (qPD), together with T1, T2 and magnetisation transfer saturation1. However, while qPD data could be very useful for clinical purposes, clinical acquisition protocols usually lack images suitable for accurate qPD measurements. In this study, qPD maps were calculated from routine clinical scans using an existing method2,3, corrected to take into account discrepancies between real and nominal values of the excitation B1 field. Results were then compared with those obtained without correction, and MPM-derived maps.

Theory

qPD, T2 and T1 maps from clinical (turbo spin-echo (TSE)) data were calculated by solving the associated Bloch equation system:

$$S_\text{PD}=\text{qPD}(1-e^{-\text{TR}_1/T_1})e^{-\text{TE}_1/T_2}$$

$$S_\text{T2}=\text{qPD}(1-e^{-\text{TR}_1/T_1})e^{-\text{TE}_2/T_2}$$

$$S_\text{T1}=\text{qPD}(1-e^{-\text{TR}_2/T_1})e^{-\text{TE}_3/T_2}$$

where Si, with i=PD,T2,T1, represents PD,T2,T1-weighted signal. For the TSE readout, the TE corresponding to the echo signal acquired along the central line of the k-space was considered as representative of the whole image2. Bias field correction was then applied to the qPD maps as described in3, where maps are normalised to the mean qPD value in the ventricular cerebrospinal fluid (CSF).

Under the hypothesis that the real B1 might not coincide with the nominal one, the expression for magnetisation recovery at time TR would be:

$$\int ^{M_z} _{\beta M_0} \frac{\text{d}M_z}{M_z-M_0}=-\int_0^\text{TR}\frac{\text{d}t}{T_1}$$

where M0 is the longitudinal magnetisation at equilibrium, and β is the fraction of longitudinal magnetisation surviving after the pulse (nominally β=0 for a perfect 90° pulse). By solving the integral, since the signal is proportional to $$$M_z(\text{TR})$$$, the system can be expressed as

$$S_\text{PD}=\text{qPD}(1-(1-\beta)e^{-\text{TR}_1/T_1})e^{-\text{TE}_1/T_2}$$

$$S_\text{T2}=\text{qPD}(1-(1-\beta)e^{-\text{TR}_1/T_1})e^{-\text{TE}_2/T_2}$$

$$S_\text{T1}=\text{qPD}(1-(1-\beta)e^{-\text{TR}_2/T_1})e^{-\text{TE}_3/T_2}$$

Methods

Acquired data: All scans were acquired on four healthy controls (1 female, mean age 34±4years), using a 3T Philips Achieva MR system, with a 32-channel head coil and multi-transmit technology. The clinical protocol comprised a PD/T2-weighted TSE(scan-time=4’02”, TE=19/85ms, TR=3.5s, 1x1x3mm) and a T1-weighted inversion recovery-TSE(scan-time=5’43”, TE=10ms, TR=625ms, 1x1x3mm).

The MPM protocol consisted of three (product) multi-echo 3D sagittal (1x1x1mm) SPGR sequences with MT-, PD- or T1-weighting (TR=18ms, flip angle ɑ=23°/4° for T1w/PDw; TR=30ms, ɑ=9°, MT-pulse ɑ=220°, duration=8ms, offset frequency=1kHz for MT-weighted, with six equidistant TE=2.4-14.4ms, SENSE=2.5, partial Fourier=5/8, FOV=256x240x170mm). B1 mapping was performed using actual flip angle imaging (AFI)(ɑ=60°, TR1/TR2/TE=30/150/2.3ms)4.

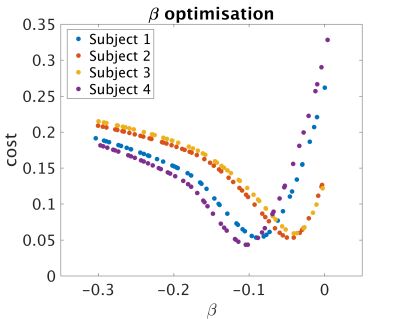
Data analysis: qPD maps were calculated for different β-values(Fig.1). After bias field correction, average qPD in white matter (WM) and grey matter (GM) were calculated for each β. A cost function was defined as the norm of the difference-vector between the obtained mean values and those found in literature (WM:0.69, GM:0.80)5. The best-β for each subject was then used to calculate the final qPD map. A second qPD map was calculated for each subject, using the average best-β across subjects.

Processing was performed using in-house written Matlab code, similarly to1,6, with T1 maps corrected for B1 errors using AFI4. Bias field correction was then applied.All qPD maps were then linearly calibrated so that the average value in WM was 0.69.

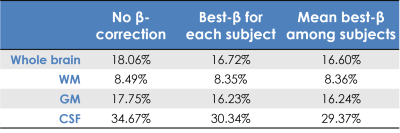
Comparison: The MPM-qPD map for each subject was considered as a reference. The root-mean-square difference (RMSD) between the clinical-qPD maps and the reference was then calculated for each of the two methods. RMSD was computed in the whole brain, WM, GM and ventricular CSF, using probabilistic masks thresholded at 99%.

Results

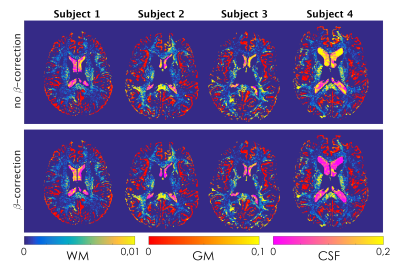
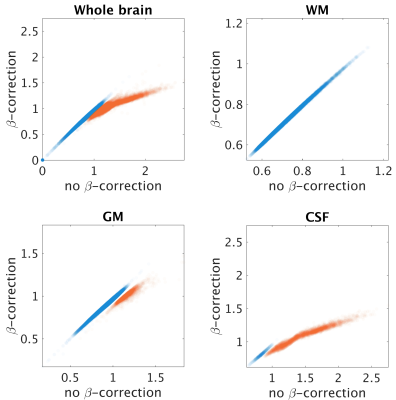
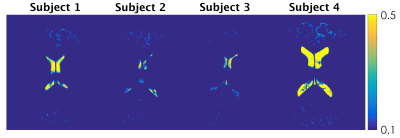
β-optimisation curves for each subjects are reported in Fig.1. Square-difference maps for the two methods, for all subjects are shown in Fig.2. Average RMSD across subjects are reported in Fig.3. Comparison between qPD maps calculated with and without β-correction is shown in Fig.4-5.

Discussion

The β-correction improves qPD maps reconstructed from clinical data, increasing their similarity to those from MPM, especially in CSF, GM and the whole brain. Using the average best-β across subjects returned similar results, which enables the use of this method in real clinical applications, where cohorts also include patients: by calculating the average best-β on the healthy controls, it would also be possible to apply β-correction in patients. Examining the correlation between the two clinical-qPD maps, image voxels seem to be divided in two pools, only one of which is affected by the β-correction (mainly in GM and CSF). Such voxels are the ones most affected by B1 inhomogeneity. The β-correction seems therefore to compensate for such bias, which is applicable to routine clinical data, without the need of additional specific quantitative sequences.

Conclusion

A revisited method for the reconstruction of qPD maps from clinical data was tested, using MPM data as reference. The proposed method seems to partially correct for B1 inhomogeneities, hence providing better results than standard clinical images.

Acknowledgements

This work is supported by the Engineering and Physical Sciences Research Council (EPSRC: EP/M020533/1); the Horizon2020-EU.3.1 (634541) grant; the UK Multiple Sclerosis Society (892/08) and the Department of Health’s National Institute for Health Research Biomedical Research Centres (BRC R&D03/10/RAG0449).

References

[1] Helms, G., Dathe, H. and Dechent, P. (2008), Quantitative FLASH MRI at 3T using a rational approximation of the Ernst equation. Magn. Reson. Med., 59: 667–672. doi:10.1002/mrm.21542

[2] Anderson, S. W., Sakai, O., Soto, J. A. and Jara, H. (2013), Improved T2 mapping accuracy with dual-echo turbo spin echo: Effect of phase encoding profile orders. Magn Reson Med, 69: 137–143. doi:10.1002/mrm.24213

[3] Volz, S., Nöth, U., Jurcoane, A., Ziemann, U., Hattingen, E., and Deichmann, R. (2012). Quantitative proton density mapping: correcting the receiver sensitivity bias via pseudo proton densities. Neuroimage; 63(1), 540-52. doi:10.1016/j.neuroimage.2012.06.076

[4] Yarnykh, V. L. (2007), Actual flip-angle imaging in the pulsed steady state: A method for rapid three-dimensional mapping of the transmitted radiofrequency field. Magn. Reson. Med., 57: 192–200. doi:10.1002/mrm.21120

[5] Tofts P. (2003). Quantitative MRI of the Brain: Measuring Changes Caused by Disease. Chichester, UK: John Wiley and Sons; doi:10.1002/0470869526

[6] Weiskopf, N., Suckling, J., Williams, G., Correia, M. M., Inkster, B., Tait, R., Ooi, C., Bullmore, E. T., Lutti, A. (2013). Quantitative multi-parameter mapping of R1, PD*, MT, and R2* at 3T: a multi-center validation. Frontiers in Neuroscience, 7, 95. doi:10.3389/fnins.2013.00095


Figures

Figure 1. β-optimisation curves. β-values go from -0.3 to 0 (nominal). The range of β was chosen by trial and error. The cost function was defined as the norm of the difference-vector between average qPD values in WM and GM, and the values found in literature: 0.69 for WM, 0.80 for GM. For all subjects, a best-β corresponding to the minimum of the cost function can be found.

Figure 2. Squared difference (SD) maps for the four subjects. On the first row: SD between uncorrected and MPM-qPD maps. On the second row: SD between β-corrected and MPM-qPD maps.

Figure 3. Average percentage RMSD across subjects. Values are expressed in percentage units respect to the MPM maps. Values obtained when comparing the uncorrected method to MPM are reported in the first column. In the second column are reported those obtained when comparing the corrected method, using for each subject its best-β. In the third column, those obtained when comparing the corrected method, using for all subject the average best-β among them.

Figure 4. Correlation plots between uncorrected and corrected qPD maps for one subject. Voxels seem to distribute in two pools, only one of which (blue) shows good correlation. The other pool (orange) is the one mainly affected by the β-correction.

Figure 5. Map of the voxels most affected by the β-correction. Intensity is proportional to the difference between the values in the uncorrected and corrected maps.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
2846