2824

Zero-padding reconstruction for wave-CAIPI images with improved accuracy, and its application in ViSTa myelin water images
Zhe Wu1, Berkin Bilgic2,3, Hongjian He1, Yi Sun4, Yiping Du5, Kawin Setsompop2,3, and Jianhui Zhong1,6

1Center for Brain Imaging Science and Technology, Department of Biomedical Engineering, Zhejiang University, Hangzhou, China, 2Athinoula A. Martinos Center for Biomedical Imaging, Department of Radiology, Massachusetts General Hospital, Charlestown, MA, United States, 3Department of Radiology, Harvard Medical School, Boston, MA, United States, 4MR Collaboration NE Asia, Siemens Healthcare, Shanghai, China, 5School of Biomedical Engineering, Shanghai Jiao Tong University, Shanghai, China, 6Department of Imaging Sciences, University of Rochester, Rochester, NY, United States

Synopsis

This study presents an intuitive zero-padding (ZP) reconstruction method for wave-encoded images with an improved accuracy. It was shown to be effective in reducing the residual point spread function (PSF) for all wave-encoded images. ZP reduced the errors between the wave-encoded and Cartesian GRE for all wave gradient configurations in simulation and reduced the side-main lobe intensity ratio from 34% to 16% in the thin-slab in vivo Visualization of Short Transverse relaxation time component (ViSTa) images. ZP is applicable for the reconstruction of wave-CAIPI, a recent proposed parallel imaging method using wave-encoding with negligible g-factor penalty under high acceleration factor.

Introduction

Wave-CAIPI [1] is a recently proposed parallel imaging technique that implements sinusoidal gradients on Gy and Gz axes during the readout period, performs wave-encoding to spread voxels along the readout axis.This increases the variation of the coil sensitivity profiles in overlapping voxels, thus enabling high reduction factors (up to 15-fold) while achieving extremely low g-factor noise penalty on sequences like GRE [1], FSE [2], and MP-RAGE [3].

In this study, we demonstrate the intra-voxel artifacts in current wave-encoded images, and propose a zero-padding (ZP) method for alleviating this problem that leads to a wave-CAIPI reconstruction with improved accuracy. The improvements of ZP for in vivo direct myelin imaging using Visualization of Short Transverse relaxation time component (ViSTa) [4] are also demonstrated.

Theory

Without loss of generality, consider the wave gradients on the partition-encoding ($$$Z$$$) axis, which usually has the largest voxel size:

$$s(k_x)=\int_{z_0-\Delta{z}/2}^{z_0+\Delta{z}/2} e^{jP_z(k_x)z}m(k_x,z)dz\qquad\qquad(1)$$

where $$$m(k_x,z)$$$ represents the spin density of this voxel in hybrid space, $$$P_z$$$ represents the k-space trajectory of the $$$Z$$$ wave gradient $$$g_z(t)$$$: $$$P_z(t)=\int_{0}^{t}g_z(\tau)d\tau$$$, and $$$t$$$ is replaced by $$$k_x$$$ for clarity as each time point corresponds to a $$$k_x$$$ location. Using the wave point spread function (PSF) on the voxel center for reconstruction, the resulting signal is:

$$\hat{s}(k_x)=e^{-jP_z(k_x)z_0}s(k_x)=\int_{z_0-\Delta{z}/2}^{z_0+\Delta{z}/2}e^{j(z-z_0)P_z(k_x)}m(k_x,z)dz\qquad\qquad(2)$$

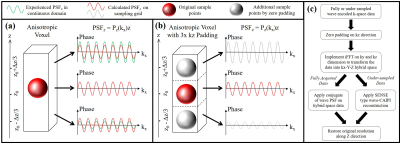
The original wave-CAIPI reconstruction [1] uses $$$z=z_0$$$ as the unique location for calculating the wave PSF of the entire voxel, and the intra-voxel integral in Eq. 2 is discarded, which does not fully comply with the real scenario as the residual phase term $$$e^{j(z-z_0)P_z(k_x)}$$$ in Eq. 2, so the omitting of the integral introduces error and artifacts in the reconstruction (Fig. 1a).

We propose ZP to be applied along the $$$k_z$$$ direction in k-space, then transforming with inverse FFT (iFFT), yielding a hybrid space ($$$k_x$$$-$$$Z$$$) with additional sampling grids along the $$$Z$$$ direction. The wave PSF for reconstruction is calculated based on this extended sampling grid, producing a more precise estimation of the wave-incurred phase (Fig. 1b). The flow chart of applying ZP method on both fully acquired and undersampled wave-encoded data is shown in Fig. 1c. The same procedure is also valid for the $$$k_y$$$ direction in k-space.

Acquisition and Reconstruction

Scanning was performed on a 3T MAGNETOM Prisma (Siemens Healthcare, Erlangen, Germany). A head phantom and two healthy female subjects (aged 27 and 25 years) were scanned:

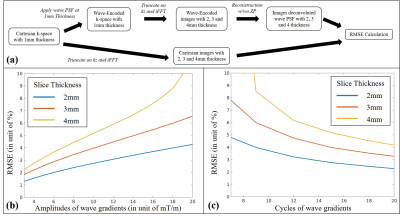
(1) Phantom: Cartesian 3D GRE scan: TR/TE/FA = 20 ms/8 ms/15 degrees, FOV 224 × 224 × 96 mm3, and 1 mm isotropic voxel size. Wave PSFs with different configurations in 1mm resolution along the Z axis was manually applied to this Cartesian data. The data were subsequently truncated in k-space to preserve the central 1/2, 1/3, and 1/4 along $$$k_z$$$ to simulate 2 mm, 3 mm, and 4 mm slice thickness, and were then reconstructed with and without ZP method. The root-mean-square errors (RMSEs) between the results and those from the Cartesian data with the same slice thickness were calculated (Fig. 2a).

(2) In vivo: thin-slab ViSTa [4]: $$$TI_1$$$ = 560 ms, $$$TI_2$$$ = 222 ms, $$$TD$$$ = 378 ms, TR = $$$TI_1$$$ + $$$TI_2$$$ + $$$TD$$$ = 1160 ms, TE = 7.15 ms, flip angle 90 degrees, acquisition matrix 192 × 192 × 8, voxel size 1.15 × 1.15 × 3 mm3, wave gradient cycle = 7, amplitude = 6 mT/m. A 2× ZP along the $$$k_y$$$ direction and a 3× ZP along the $$$k_z$$$ direction were applied during reconstruction.

Results and Discussion

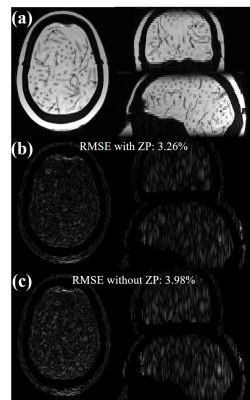
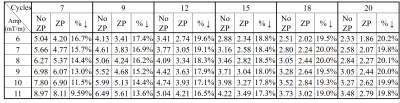
Figs. 2b and 2c show the RMSEs vs. wave gradient amplitudes (cycle = 15) and RMSEs vs. wave cycles (amplitude = 10 mT/m) using original wave-CAIPI reconstruction. Table 1 compares the RMSE with and without ZP for multiple wave gradient configurations in a simulated 3mm slice thickness. The improvement brought by ZP is consistent for all these cases. For a wave gradient of 10 mT/m, 15 cycles, 3 mm thickness, the 3× ZP reconstruction reduced RMSE from 3.98% to 3.26% (Fig. 3).

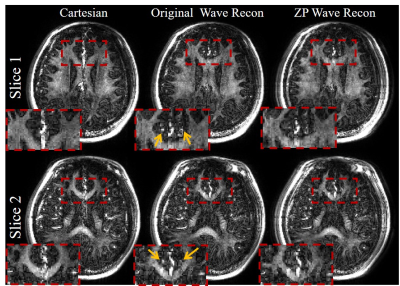
Fig. 4 show a significant reduction in the residual wave PSF artifacts in the in vivo thin-slab wave-encoded ViSTa images when ZP methods were used for reconstruction. The artifacts on the small vessels (yellow arrows) are almost invisible with the ZP method. On slice 1 in Fig. 4, the ratio between the mean intensity of the side lobes and that from the main lobe decreases from 34% to 16 % with the ZP method.

Conclusion

RMSE between wave-encoded and Cartesian images is correlated with the k-space wave radius: it grew as the wave amplitude or voxel size increased, whereas it decreased when the wave cycle increased. ZP reduced this RMSE in all wave gradient configurations, yielding a reconstruction for wave-encoded images with improved accuracy.

Acknowledgements

This work was supported by the National Key R&D Program of China (2017YFC0909200), National Natural Science Foundation of China (81401473, 91632109, 81371518) and the Fundamental Research Funds for the Central Universities (2017QNA5016).

References

[1] Bilgic B, Gagoski BA, Cauley SF, Fan AP, Polimeni JR, Grant PE, Wald LL, Setsompop K. Wave-CAIPI for highly accelerated 3D imaging. Magn. Reson. Med. 2015;73:2152–2162. doi: 10.1002/mrm.25347.

[2] Gagoski BA, Bilgic B, Eichner C, Bhat H, Grant PE, Wald LL, Setsompop K. RARE/turbo spin echo imaging with simultaneous multislice Wave-CAIPI. Magn. Reson. Med. 2015;73:929–938. doi: 10.1002/mrm.25615.

[3] Polak D, Setsompop K, Cauley SF, Gagoski BA, Bhat H, Maier F, Bachert P, Wald LL, Bilgic B. Wave-CAIPI for highly accelerated MP-RAGE imaging. Magn. Reson. Med. 2017;0:1–6. doi: 10.1002/mrm.26649.

[4] Oh S-H, Bilello M, Schindler M, Markowitz CE, Detre JA, Lee J. Direct visualization of short transverse relaxation time component (ViSTa). Neuroimage 2013;83:485–492. doi: 10.1016/j.neuroimage.2013.06.047.

Figures

Fig.1. Principle and flow chart of the ZP method on an anisotropic voxel centering at $$$z_0$$$ and with resolution $$$\Delta{z}$$$. (a) The experienced wave PSF within the voxel is varying from their physical location in continuous space. The wave PSF of this voxel (red wave) calculated by the location of voxel center (red ball) was different from the real ones (green wave), introducing residual wave PSF artifacts. (b) Two additional $$$\Delta{z}/3$$$ shifted sample points (silver ball) were obtained after 3× ZP, which reduced the mismatch between the real and calculated wave PSF (red/silver waves) and alleviated artifacts. (c) Flow chart of the ZP reconstruction method.

Fig. 2. (a) Processing procedure of the RMSE calculation for the manually wave-encoded images with slice thickness of 2, 3, and 4 mm by k-space truncation. (b) RMSEs vs. wave gradient amplitudes, with 15 cycles. (c) RMSEs vs. wave cycles, with wave amplitude of 10 mT/m.

Fig. 3. GRE phantom images. (a) Cartesian GRE original images, with a voxel size of 1×1×3mm3. (b) and (c) difference maps between the Cartesian GRE and reconstructed wave-encoded GRE, with (b) and without (c) ZP, using wave gradients with 15 cycles and an amplitude of 10 mT/m.

Fig. 4. Comparing residual wave PSF artifacts in ViSTa images between the original and ZP (2× ZP on $$$k_y$$$, and 3× ZP on $$$k_z$$$) reconstruction for wave-encoded images. The Cartesian acquired ViSTa images were used as the ground truth. Artifacts were observed in the results of the original wave reconstruction method (yellow arrows), but were alleviated substantially with the proposed method. For slice 1, the ratio between the intensities of the side lobes and the main lobe was reduced from 34% to 16% with ZP.

Table 1 RMSE w/wo ZP for 3D wave GRE using different wave gradient configurations with 3mm slice thickness (unit in percentages), and the relative reduction of RMSE brought by ZP compared to the results w/o ZP.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
2824