Synopsis

Phase contrast MRI (PC-MRI) has been evolved into a practical and widely used technique for quantification of blood flow velocity and volume, which provides useful insights into pathophysiology. However, PC-MRI requires a long acquisition time to build up phase contrast, requiring flow-reference and flow-encoded datasets over multiple heartbeats, and limiting its general use of flow imaging as a clinical routine. To enable higher acceleration rates, in this work we proposed a generalized coil-by-coil approach to simultaneous multislice (SMS) reconstruction in conjunction with inplane acceleration called as bline SMS (b-SMS) by incorporating slice separation and inplane reconstruction into a single optimization framework that is formulated as an inverse problem with data fidelity.

Introduction

Phase contrast MRI (PC-MRI) has been evolved into a practical and widely used technique for quantification of blood flow velocity and volume, which provides useful insights into pathophysiology^1-3. However, PC-MRI requires a long acquisition time for flow-reference and flow-encoded datasets over multiple heartbeats, limiting the general use of flow imaging in routine clinical MR exams. To enable higher acceleration rates, we propose a generalized coil-by-coil approach for simultaneous multislice (SMS) reconstruction in conjunction with inplane acceleration, here referred to as blind SMS (B-SMS), which incorporates slice separation and inplane reconstruction into a single optimization framework that is formulated as an inverse problem with data fidelity.

Methods

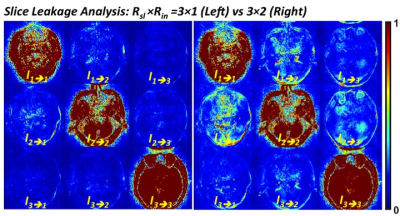
Inplane Reconstruction and Slice Separation: GRAPPA concepts^4-5 have been widely used for separating multiple slices from SMS acquisition as well as filling missing signals from partial measurement without the need of explicit coil sensitivities, in which coil-by-coil reconstruction is performed by synthesizing k-space data of interest from neighboring data in k-space across coils once it synthesizing kernels are estimated in calibration step. From this view, SMS k-space data with inplane acceleration can be reconstructed by sequentially solving forward problems for each direction as follows: $$\mathcal{I}_s=\mathbf{G}^p\mathbf{G}^m\mathcal{Y} \tag{1}$$ where $$$\mathcal{Y}$$$ is a vector of acquired SMS k-space data, and $$$\mathbf{G}^p$$$ and $$$\mathbf{G}^m$$$ are block convolution matrices for SMS and inplane kernels, respectively. Although this sequential approach unfolds bi-directional aliasing, it is susceptible to error propagation through the layer of the forward problems. Figure 1 shows simulated error examples using slice leakage analysis without and with inplane acceleration, demonstrating that reduced field-of-view (FOV) from undersampling leads to significant slice leakage artifacts compared those without undersampling.

SMS Encoding: An SMS excitation can be formulated as a linear combination of all excited slices with its phase offset terms⁶: $$\mathcal{I}_s=\sum_s \mathcal{I}_s \cdot e^{-2\pi i(s-1)/N_s}\tag{2}$$ where $$$\mathcal{I}_a$$$ is a vector of underlying SMS k-space data. By applying inplane acceleration to the underlying SMS data, data acquisition is: $$\mathcal{Y}=\mathbf{M}\mathbf{F}^{sl}_u \mathcal{I}_s \tag{3}$$ where $$$\mathbf{F}^{sl}_u$$$ is the undersampled Fourier transform along slice direction, and $$$\mathbf{M}$$$ is the undersampling mask in the inplane direction. To ensure consistency of the estimated slice data to its acquired SMS data, the SMS encoding is used as a data fidelity.

Optimization for Blind SMS Reconstruction: Since both slice and inplane accelerations compete with each other, its combination approach typically limits the maximum achievable acceleration. In this work, simultaneous estimations of the underlying aliased data and its individual slice data are taken into account to alleviate a tradeoff between both acceleration directions, which is formulated with data fidelity: $$\underset{\mathcal{I}_s,\mathcal{I}_a}{\mathrm{argmin}} \; \; \frac{1}{2}\left \| \mathcal{Y} - \mathbf{M} \mathbf{F}^{sl}_{u} \mathcal{I}_s \right \|^2_2 + \lambda \left \| \mathcal{I}_{s} - \mathbf{G}^{p}\mathbf{G}^{m}\mathcal{I}_a \right \|^2_2 \tag{4} $$ where λ is a balancing parameter between data consistency and calibration consistency. With the estimation of the underlying aliased data $$$\mathcal{I}_a$$$, slice separation $$$\mathbf{G}^{m}\mathcal{I}_a$$$ should be ideally consistent with $$$\mathcal{I}_s$$$, while the relationship between $$$\mathcal{I}_a$$$ and $$$\mathcal{I}_s$$$ is inherently in Eq. (2). In this regard, Eq. (4) must satisfy the two constraints, which can be rewritten as: $$\underset{\mathcal{I}_s,\mathcal{I}_a}{\mathrm{argmin}} \; \; \frac{1}{2}\left \| \mathcal{Y} - \mathbf{M} \mathcal{I}_a \right \|^2_2 + \lambda \left \| \mathcal{I}_{s} - \mathbf{G}^{p}\mathcal{I}_s \right \|^2_2 \tag{5} \\ s.t. \;\;\; \mathbf{F}^{sl}_{u} \mathcal{I}_s=\mathcal{I}_a \;\; \mathrm{and} \;\; \mathcal{I}_s=\mathbf{G}^{m}\mathcal{I}_a$$

To find its solutions, the alternating minimization method is employed by decomposing Eq. (5) into two subproblems.

Results

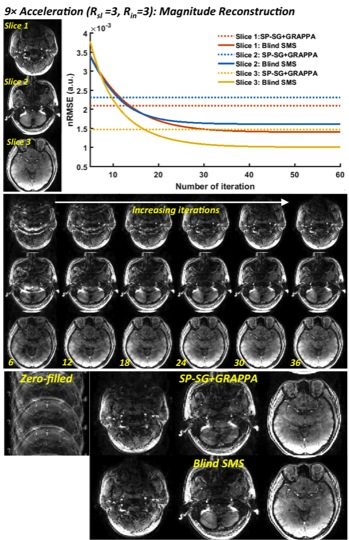
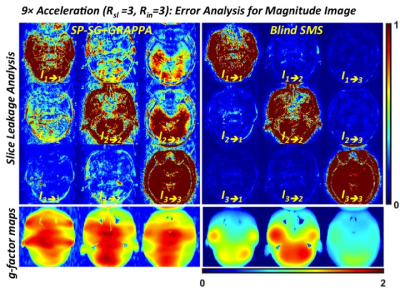
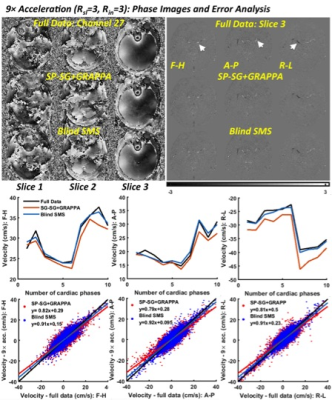
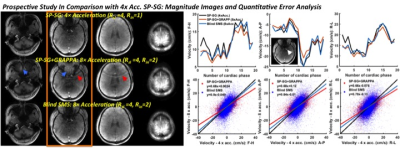
To validate the proposed B-SMS reconstruction on both magnitude and phase images, simulations and experimental studies were performed with a 32-channel head coil using the retrospectively emulated and prospectively acquired SMS PC datasets. Figures 2-4 show the reconstruction results of the simulation at R=9-fold acceleration (R_sl=3 and R_in =3). Figure 2 shows nRMSEs and reconstructed images as a function of iterations in comparison with combination approach of split-slice GRAPPA and conventional GRAPPA (SP-SG+GRAPPA). B-SMS outperforms SP-SG+GRAPPA in suppressing aliasing artifacts and noises, which shows a error example corresponding to the slice leakage and g-factor maps in Fig. 3. Figure 4 shows PC images and its statistical analysis for flow measurements, demonstrating that the velocity measurements in B-SMS are strongly correlated with those in full data more than those in SP-SG+GRAPPA. Figure 5 shows the results of the prospective acquisition at R=8-fold acceleration (R_sl=3 and R_in=2), which exhibits a tendency similar to the above simulations.

Discussions and Conclusions

Acknowledgements

References

1. Firmin DN, Nayler GL, Klipstein RH, Underwood SR, Rees RSO, Longmore DB. In vivo validation of MR velocity imaging. J Comput Assist Tomogr 1987; 11:751-756.

2. Pelc NJ, Herfkens RJ, Shimakawa A, Enzmann DR. Phase contrast cine magnetic resonance imaging. Magn Reson Q 1991; 7:229-254.

3. Lee AT, Pike GB, Pelc NJ, Three-point Phase contrast velocity measurements with increased velocity-to-noise ratio. Magn Reson Med 1995; 33:122-126.

4. Griswold MA, Jakob PM, Heidemann RM, Nittka M, Jellus V, Wang J, Kiefer B, Haase A. Generalized autocalibrating partially parallel acquisition (GRAPPA). Magn Reson Med 2002; 47: 1202-1210.

5. Cauley SF, Polimeni JR, Bhat H, Wald LL, Setsompop K. Interslice leakage artifact reduction technique for simultaneous multislice acquisitions. Magn Reson Med 2014; 72:93-102

6. Zahneisen B, Poser BA, Ernst T, Stenger VA. Three-dimensional Fourier encoding of simultaneously excited slices: Generalized acquisition and reconstruction framework. Magn Reson Med 2014;71:2071-2081.