2821
A Fast and General Non-Cartesian GRAPPA Reconstruction Method1University of Michigan, Ann Arbor, MI, United States
Synopsis
Iterative parallel imaging reconstruction can be very time-consuming for dynamic imaging applications such as functional MRI. GRAPPA is non-iterative but is generally not well-suited for non-Cartesian acquisitions. In this work, we propose a generalization of GRAPPA applicable to arbitrary non-Cartesian readouts. Our non-Cartesian GRAPPA method works by associating a unique kernel with each unsampled (missing) k-space location, and synthesizing non-Cartesian autocalibration (ACS) data by phase-shifts. This approach requires calibrating a very large number of distinct patterns, for which we propose an efficient NUFFT-like algorithm. With this approach we demonstrate fast reconstruction of 3D stack-of-spirals and stack-of-stars images.
Introduction
GRAPPA1 is a non-iterative Parallel Imaging (PI) technique that, unlike SENSE, does not require explicit knowledge of coil sensitivity maps (i.e., is auto-calibrating). However, GRAPPA generally assumes Cartesian k-space sampling, and direct application of GRAPPA to arbitrary non-Cartesian trajectories is not possible. Partial workarounds for specific readout trajectories have been proposed, e.g., segmenting spiral trajectories into “wedges” that undergo rectilinear GRAPPA2, or GROG gridding3, an approximate interpolation scheme. However, a general GRAPPA reconstruction approach for arbitrary 2D/3D non-Cartesian sampling does not yet exist.
Here we propose a general non-Cartesian GRAPPA reconstruction that is not restricted to specific readout trajectories. It works by assigning a unique kernel to each unsampled k-space point. To keep computational costs down, we propose an efficient NUFFT-based algorithm4. We apply our method to the reconstruction of 3D stack-of-stars/spirals datasets.
Methods
GRAPPA first identifies all (unique) kernel patterns to be calibrated (Fig.1). Then, for each pattern, all combinations of autocalibration signals (ACS) that match the pattern are obtained. These combinations become the rows of $$$\tilde{\mathcal{A}}≔[\tilde{A}_1,…,\tilde{A}_{N_c}]∈\mathbb{C}^{N_k×N_c⋅N_n},\tilde{\ell}≔[\tilde{l}_1,…,\tilde{l}_{N_c}]∈\mathbb{C}^{N_k×N_c}$$$, whose columns are ordered by coils and elements’ positions within the kernel ($$$N_k,N_c,N_n$$$ are number-of-combinations/coils/neighbors). Then, the corresponding GRAPPA weights is the solution to the least squares (LS) problem,
$$\eqalignno{\arg_{w_c}\min‖\tilde{\mathcal{A}}w_c-\tilde{l}_c‖^2&⇒&w_c^⋆=\tilde{\mathcal{A}}^{+}\tilde{l}_c=(\tilde{\mathcal{A}}^\mathsf{H}\tilde{\mathcal{A}})^{-1}\tilde{\mathcal{A}}^\mathsf{H}\tilde{l}_c&\tag{1}}$$
where c indexes coils.
For arbitrary non-Cartesian readouts, where each unsampled k-space location generally has a unique pattern of sampled neighbors, it is in general not feasible to acquire the necessary ACS data for every unsampled location. Our approach is therefore to synthesize off-grid ACS data (for each unsampled location) from a Nyquist-sampled ACS k-space region, by using the phase-shift property of the Fourier transform (FT) (Fig.1d) such that Eq.1 can be applied (Fig.1c). This approach is general as it puts no requirement on readout trajectory, and can be fully automated, i.e., it requires no manual intervention to specify k-space wedges or other trajectory-specific information.
The main drawback of this approach is increased computational and storage costs, since for each unsampled k-space location, ACS data must be synthesized and Eq.1 must be solved. To address this computational issue, we propose a novel algorithm for obtaining the kernel weights from Eq.1. Specifically, we treat the ACS region as having circulant boundary conditions, i.e., we allow ACS data to wrap around as needed to form matches for the pattern being calibrated. When the ACS region is sufficiently large, we hypothesize that the wraparounds have negligible impact on reconstruction quality. Due to the circulant boundary, $$$\tilde{\mathcal{A}}_c$$$’s columns are circularly (phase) shifted replicas of $$$\tilde{l}_c$$$. Then, an image domain view of the solution to Eq.1 is:
$$\eqalignno{w_c^⋆=(\tilde{\mathcal{A}}^\mathsf{H}(\mathcal{F}\mathcal{F}^\mathsf{H})\tilde{\mathcal{A}})^{-1}\tilde{\mathcal{A}}^\mathsf{H}(\mathcal{F}\mathcal{F}^\mathsf{H})\tilde{l}c=(\mathcal{A}^\mathsf{H}\mathcal{A})^{-1}\mathcal{A}^\mathsf{H}l_c=([A_1,…,A_{N_c}]^\mathsf{H}[A_1,…,A_{N_c}])^{-1}[A_1,…,A_{N_c}]^\mathsf{H}l_c&\tag{2}}$$
where unitary matrix $$$\mathcal{F}$$$ is a properly sized FT. Converted by FT, $$$A_c$$$’s columns are (low-resolution coil images) $$$l_c$$$ modulated by linear phases. As pointwise products of two linear phases is another a linear phase, we have (Fig.2):
$$$A_i(:,m)^\mathsf{H}A_j(:,n)=⟨\text{diag}(ν_m)l_i,\text{diag}(ν_n)l_j⟩=⟨\text{diag}(ν_n)ν_m,\text{diag}(l_i)l_j⟩≕⟨ν_{nm},l_{ij}⟩\tag{3}$$$
where $$$i,j$$$ are coil indices, and m,n are column indices of $$$A_i,A_j$$$. In other words, these entries are (spatial) frequency components of $$$l_{ij}$$$, which are pairwise products of low-resolution coil images (Fig.2c). The $$$l_{ij}$$$ are shared among all kernel patterns and only need to be computed once. We propose to exploit this by first zero-padding $$$l_i$$$ (equivalently $$$l_{ij}$$$), thus preparing a finely sampled spectrum. Good approximations to $$$\mathcal{A}^\mathsf{H}\mathcal{A}$$$ and $$$\mathcal{A}^\mathsf{H}l_c$$$ can then be efficiently computed (for arbitrary non-Cartesian pattern) by simple interpolations with small interpolation kernels (bilinear), instead of expensive dense matrix multiplications. This reduces computation complexity from $$$Θ(N_kN_c^2N_n^2+N_kN_cN_n)$$$ to $$$Θ(N_c^2N_n^2+N_cN_n)$$$, where $$$N_k$$$ is typically a few thousand for 3D calibration (e.g., ACS size 20×20×10).
Results
Figures 3-4 compare our method with the commonly used conjugate gradient SENSE (cg-SENSE) on two 3D non-Cartesian data sets (stack-of-stars and stack-of-spirals). We reconstructed both data sets without changing the reconstruction code in any way. Different PI acceleration factors are achieved by retrospective undersampling (skipping spokes or interleaves). Our approach reconstructs images with comparable quality to cg-SENSE, using image-error or g-factor metrics, while our approach (6secs/frame) is much faster than cg-SENSE (2mins/frame) due to its non-iterative nature. The NUFFT idea reduces calibration time from 40mins to 2mins (detailed sequence setups are described in the figure captions.)Discussion and Conclusions:
Our results show that the proposed general, non-iterative, non-Cartesian GRAPPA algorithm can rival cg-SENSE in image quality. For reconstructing an fMRI (time-series) data set, our approach provides a fast alternative to cg-SENSE. Storage of GRAPPA kernel weights may impose high memory demands for, e.g., high-resolution imaging with a high coil count, and may benefit from coil compression.Acknowledgements
This work is supported by NIH grants R01EB023618 and R21EB019653.References
- Griswold, Mark A. et al. “Generalized Autocalibrating Partially Parallel Acquisitions (GRAPPA).” Magnetic Resonance in Medicine 47.6 (2002): 1202–1210.
- Heidemann, Robin M. et al. “Direct Parallel Image Reconstructions for Spiral Trajectories Using GRAPPA.” Magnetic Resonance in Medicine 56.2 (2006): 317–326.
- Seiberlich, Nicole et al. “Reconstruction of Undersampled Non-Cartesian Data Sets Using Pseudo-Cartesian GRAPPA in Conjunction with GROG.” Magnetic Resonance in Medicine 59.5 (2008): 1127–1137.
- Fessler, Jeffrey A., and B.P. Sutton. “Nonuniform Fast Fourier Transforms Using Min-Max Interpolation.” IEEE Transactions on Signal Processing 51.2 (2003): 560–574.
Figures
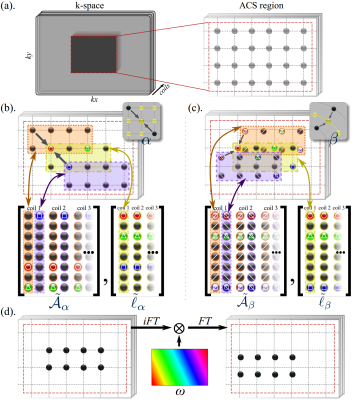
Figure 1: Constructing Cartesian and non-Cartesian GRAPPA calibration matrices. (a) On-grid ACS-data from dense-sampling (or gridding). (b) Calibration for a simple Cartesian kernel pattern $$$\alpha$$$ with, $$$N_n=2$$$ neighbors used to reconstruct the center. One can obtain $$$N_k=8$$$ combinations from the ACS region that match the relative positions described by the pattern. Neighbors and centers are separated into matrices, $$$\tilde{\mathcal{A}}_\alpha≔[\tilde{A}_1,…,\tilde{A}_{N_c}],\tilde{\ell}≔[\tilde{l}_1,…,\tilde{l}_{N_c}]$$$, where $$$\tilde{\mathcal{A}}_c∈\mathbb{C}^{N_k×N_n},\tilde{l}_c∈\mathbb{C}^{N_k},c=1,…,N_c$$$. Then for coil $$$c$$$, least squares problem $$$\arg_{w_c}\min‖\tilde{\mathcal{A}}w_c-\tilde{l}_c‖^2$$$ gives GRAPPA weights $$$w_c^⋆=(\tilde{\mathcal{A}}^\mathsf{H}\tilde{\mathcal{A}})^{-1}\tilde{\mathcal{A}}^\mathsf{H}\tilde{l}_c$$$. (c) Non-Cartesian off-grid kernel pattern $$$\beta$$$ has no direct match in the on-grid ACS-data; instead, they are synthesized through phase-shifts. (d) Phase-shift by linear phase $$$ω$$$.
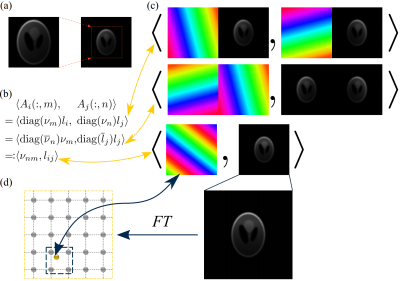
Figure 2: NUFFT-based efficient calibration algorithm using pairwise coil-image products. (a) Zero-padding (in image-space) of a low-resolution coil-image $$$l_i$$$. (b) Computation of an element of $$$\mathcal{A}^\mathsf{H}\mathcal{A}$$$, which is the inner product between a column of $$$A_i$$$ and a column of $$$A_j$$$. Circulant boundary makes these columns the phase-modulated low-resolution coil-images. (c) Visualization of (b). Linear-phases and coil-images are combined (after conjugation). (d) Due to the zero-padding, the spectrum is finely gridded, such that the frequency component corresponding to the combined linear phase ($$$\nu_{nm}$$$) can be interpolated with a small kernel (bilinear) from the fixed spectrum-profile that is shared across patterns.
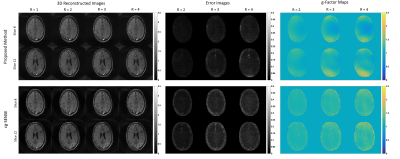
Figure 3: Stack-of-stars reconstruction results. 3D reconstruction quality comparison between the proposed non-Cartesian GRAPPA (upper row) and cg-SENSE (lower row). Panels from left to right show reconstructions with different retrospective acceleration factors (R=1,2,3,4), error images against a fully sampled reconstruction, and g-Factor maps. 2 slices are selected out of 20. Our non-Cartesian GRAPPA exhibits comparable reconstruction quality to cg-SENSE. [GE 3T scanner; 8-channel receive array; 20 kz-plates each composed of 315 spokes; FOV 20x20x20 cm3; matrix 200x200x20; flip angle 30°; TR 15ms; minimum TE.]
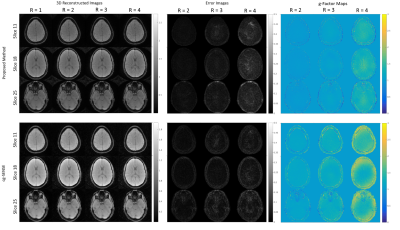
Figure 4: Stack-of-spirals reconstruction results. 3 slices are selected out of 40. Without modifying our algorithm and implementation, our non-Cartesian GRAPPA again exhibits comparable reconstruction quality to cg-SENSE. [GE 3T scanner; 8-channel receive array; 40 plates each composed of 60 spokes, FOV 22x22x20 cm3; matrix 200x200x40, flip angle 8°, TR 15ms, minimum TE.]