2819
Phase sensitive receiver combination using prescan singular value decomposition derived receiver sensitivities1Medical Biophysics, The University of Western Ontario, London, ON, Canada, 2Centre for Functional and Metabolic Mapping, The University of Western Ontario, London, ON, Canada
Synopsis
Phase sensitive imaging with multi-channel radio-frequency arrays requires sophisticated channel combination. Combining signal from multiple channels without considering the spatial sensitivity profile of those channels can lead to destructive interference and poor quality phase images. This work outlines a phase combination method which interpolates SVD derived relative sensitivity estimates from a prescan using a solid harmonic basis to allow for phase alignment that is extensible to the remainder of the imaging session. Furthermore, this phase alignment method is computationally efficient and applicable to any coil configuration.
Introduction
Interest in the contrasts available from phase images has increased in recent years1,2, parallel to the development of multi-channel radio frequency (RF) arrays for accelerated imaging. RF arrays present a particular problem for phase imaging as suboptimal combination will lead to destructive interference and poor image quality. Existing phase methods commonly rely on a post-acquisition combination of multiple images, one example is Singular Value Decomposition (SVD) combination3. SVD combination utilizes a set of images to find the relative sensitivities for an RF array, phase aligns the images using those sensitivities, and combines the images using a complex sum. This post-acquistion operation is time consuming and conventionally done voxelwise leading to high computational costs. However, it is possible to use the SVD of a low-resolution prescan to determine these relative sensitivities and align the phase of a larger image set in real time while the imaging is being completed. This is achieved through the use of solid harmonic interpolation and provides computationally efficient, real-time, phase sensitive coil combination.Methods
The prescan used to derive relative sensitivity estimates via SVD was a 10 image 8mm isotropic prescan and is routinely collected as part of the $$$B_1^+$$$ shimming protocol. Once calculated, these relative sensitivity estimates were globally corrected for shared signal. This was done to ensure that the sensitivities did not contain extraneous phase from other sources, e.g. $$$B_0$$$ and $$$B_1^+$$$, prior to solid harmonic interpolation. Relative sensitivities were fit to the solid harmonics using an iterative least squares fitting algorithm which also removes a common complex scaling term every iteration in order to move the sensitivities closer to the solid harmonic solution and improve interpolation. This fitting process consistently takes under ten seconds. These fits can be stored as coefficients of solid harmonics and permit interpolation of relative sensitivities to any image size. This interpolation can be used to align the phases of the receiver channels in subsequent acquisitions for improved phase sensitive combination. This method is more computationally efficient than performing SVD combination on every image set collected.
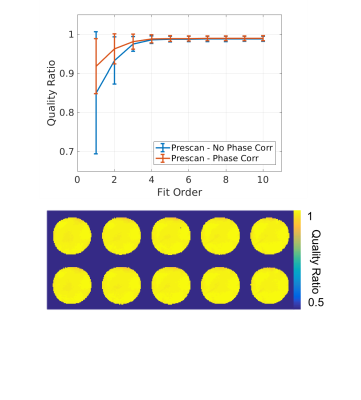
Three image sets were examined to determine the effectiveness of the proposed phase combination algorithm, two sets in human subjects and one set in an oil phantom. All images were collected on the Siemens Magnetom 7T head-only MRI system located at the Centre for Functional and Metabolic Mapping . Human data was collected with the approval of the University of Western Ontario Research Ethics Board. The oil phantom data was collected using a multi-echo gradient echo sequence (3mm isotropic voxels, 12 echos, TE=3.11 ms-53.38 ms, FA=10 , TR=100 ms) and a symmetric whole head coil with 32 receive channels5. The human data was collected using a multiband EPI sequence4 (2 mm isotropic voxels, TE=20 ms, FA=45 , TR=1.25 s, multiband factor 3 and GRAPPA factor 3) and two coils, the same symmetric whole head coil and an asymmetric coil with 32 receive channels targeting the occipital parietal region6. The efficacy of the method was evaluated using a quality ratio, a modification of the quality factor7, where the denominator is the SVD combined image as opposed to the summed magnitudes. This removes the effect of noise bias from the quality factor.
Results
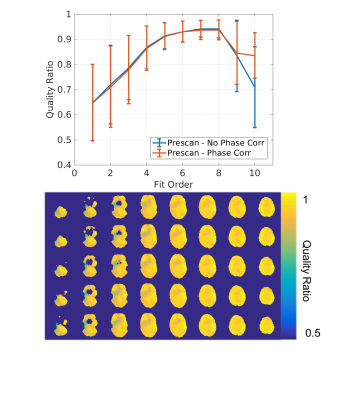
Examples of the combination in an oil phantom and in a human are displayed in Figures 1 and 2 respectively. Figure 2 shows that this method successfully removes the phase singularity caused by direct complex sum combination. Figure 3 shows the quality ratio across the oil phantom at multiple orders as well as the quality ratio image for the optimal order of 5. At this optimal order, phase sensitive combination explains 98% of the variance in the relative sensitivities and the quality ratio across the phantom was 0.989 ± 0.007 (mean ± std). In whole head coil human images, where 97% of the variance is explained, the mean quality ratio is 0.938±0.038 across the brain (Figure 4) at optimal order 7. The combined phase of an asymmetric coil design shown in Figure 5, demonstrates that this method can be used to model receiver phases even in a non-symmetric coil configuration.Discussion and Conclusions
This method allows for a phase sensitive combination to be used for multiple scans during an imaging session. It is computationally efficient, requires minimal computer storage, and is fully automated. Using solid harmonic fitting to interpolate SVD derived relative coil sensitivities from a prescan can align the phases of any data obtained during the remainder of an imaging session.Acknowledgements
This work was supported by the Natural Sciences and Engineering Research Council Discovery Grant to Dr. Ravi MenonReferences
1. Fan AP, Govindarajan ST, Kinkel RP, et al. Quantitative oxygen extraction fraction from 7-Tesla MRI phase: reproducibility and application in multiple sclerosis. J. Cereb. Blood Flow Metab. 2015;35:131–139.
2. Reichenbach JR, Schweser F, Serres B, Deistung A. Quantitative Susceptibility Mapping: Concepts and Applications. Clin. Neuroradiol. 2015;25 Suppl 2:225–230.
3. Walsh DO, Gmitro AF, Marcellin MW. Adaptive reconstruction of phased array MR imagery. Magn. Reson. Med. 2000;43:682–690.
4. Moeller S, Yacoub E, Olman CA, et al. Multiband multislice GE-EPI at 7 tesla, with 16-fold acceleration using partial parallel imaging with application to high spatial and temporal whole-brain fMRI. Magn. Reson. Med. 2010;63:1144–1153.
5. Gilbert KM, Gati JS, Kho E, et al. An parallel-transmit, parallel-receive coil for routine scanning on a 7T head-only scanner. Proc. Intl. Soc. Mag. Reson. Med. 2015.
6. Gilbert KM, Gati JS, Menon RS. Occipital-Parietal Coil with variable-density element distribution for 7T functional imaging. Proc. Intl. Soc. Mag. Reson. Med. 2017;25.
7. Robinson SD, Bredies K, Khabipova D, et al. An illustrated comparison of processing methods for MR phase imaging and QSM: combining array coil signals and phase unwrapping. NMR Biomed. 2017;30.
8. Abdul-Rahman HS, Gdeisat MA, Burton DR, et al. Fast and robust three-dimensional best path phase unwrapping algorithm. Appl. Opt. 2007;46:6623–6635.
Figures