2816

Automatic Selection of Optimal Regularization Parameters in Compressed Sensing using No Reference Magnetic Resonance Image Quality Assessment.
Kihun Bang1,2, Jinseong Jang1, Yohan Jun1,2, Hanbyol Jang1,2, Hojoon Lee3, and Dosik Hwang1

1Yonsei University, Seoul, Republic of Korea, 2Philips Korea, Seoul, Republic of Korea, 3Department of Radiology and Research Institute of Radiological Science, Yonsei University College of Medicine, Seoul, Republic of Korea

Synopsis

Compressed Sensing can reconstruct image without artifacts from the undersampled data, however setting the regularization parameters in CS optimization problem is difficult. Empirically selected parameters or extracted from L-curve method have less reliability. This abstract proposes CS reconstructed MR image quality assessment without ground truth and it can select proper regularization parameters automatically much faster and much reliable.

Purpose

Reducing the scan time in MRI is very important. Acquiring fewer measurement is the easiest way for fast scan, but insufficient sampling leads degrading of image quality or some artifacts in image. Compressed Sensing(CS) can reconstruct image without artifacts from under sampled data1. To reconstruct image from CS method, there is a minimization problem consisting of several terms and choosing their regularization parameters properly is required. Setting regularization parameters empirically couldn’t reconstruct the best image and L-curve method has some limit such as smooth problem, time-consuming2. Akasaka et al. proposed a method that select the proper regularization parameters by evaluating the images by SSIM3, however, we do not acquire full-sampled data which would be a ground truth image, we cannot evaluate the image quality in vivo. Jang et al. proposed QEMDIM, evaluating the MR images without ground truth4, and Bang et al. proposed choosing the proper regularization parameters by evaluating CS reconstructed images by QEMDIM5, but it is not optimized in CS. This abstract proposes a Compressed Sensing Magnetic Resonance Image Quality (CSMRIQ) assessment metric in order to evaluate the quality of reconstructed images from CS without ground truth. Furthermore, choosing the proper regularization parameters automatically by evaluating the CS reconstructed images from the NR-CSIQA.

Methods

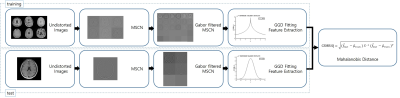
NIQE is a NR-IQA metric using Natural Scene Statistics(NSS) of spatial domain. Mean Substracted Contrast Normalized(MSCN) and its pair products have some statistics and Euclidean Distance of features is the quality score6. QEMDIM considered characteristics of MRI. Most of the artifacts in MRI caused by under-sampling has stripe patterns(e.g. Aliasing artifact, Motion artifact, Streak artifact) and uses Multi-Directional filters instead of pair products to evaluate MR image. multi-directional filters are suitable for stripe artifacts but cannot consider any sharpness and blurness. CS reconstructed image could be blur and in order to consider both directional artifacts and blurness, NR-CSIQA uses gabor filtering to decompose MSCN into 13 zone(4 scales and 4 orientations).

$$ gabor(x,y;\lambda,\theta,\psi,\sigma,\gamma)=exp(\frac{-{x^{'}}^{2}+{\gamma}^{2}{y^{'}}^{2}}{2{\sigma}^{2}})cos(2\pi\frac{x^{'}}{\lambda}+\psi)$$

$$x^{'}=xcos\theta+ysin\theta$$

$$y^{'}=-xsin\theta+ycos\theta$$

Next, fit Gabor Filtered MSCN coefficients into the Generalized Gaussian Distribution and total 28 parameters could be extracted(2 shape parameters each 1 MSCN with 13 Gabor Filtered MSCN). There are 28 parameters with 14 zones and their weight for evaluate the quality would be different, so the weights are set by inverse covariance matrix and score was calculated by mahalanobis distance. For training the metric, database was provided T2-FLAIR brain image from ADNI7. Figure 1 shows process of CSMRIQ.

$$CSMRIQ=\sqrt{(\overrightarrow{f}_{test} -\overrightarrow{\mu}_{train}) S^{-1}(\overrightarrow{f}_{test} -\overrightarrow{\mu}_{train})^{T}}$$

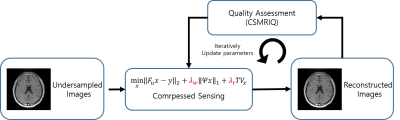
Performance of CSMRIQ are evaluated by comparing with SSIM and subjective score from radiologist. 36 T1-weighted(TR=2000ms,TE=10ms), 36 T2-weighted(TR=9000ms,TE=135ms) brain images were used for test and retrospectively Cartesian undersampling with R=2. In our experiment, CS optimization problem have 3 terms; data consistency, sparsity, total variation, and 2 regularization parameters $$$\lambda_w$$$,$$$\lambda_t$$$. Optimizing $$$\lambda_w$$$,$$$\lambda_t $$$ is our goal and CSMRIQ is exploited. First, set the regularization parameters initially random, and reconstruct image. By evaluating the image with CSMRIQ, update the regularization parameters by gradient descent method. Optimized regularization parameters could be chosen by performing these steps iteratively. The entire process of optimizing the regularization parameters are shown in figure 2.

$${\lambda_t}^{i+1}={\lambda_t}^{i}-\alpha\times\frac{\partial}{\partial\lambda_t}CSMRIQ({\lambda_w}^{i},{\lambda_t}^{t}),~~~~~~~~~~~~~~~~~~~~~ {\lambda_w}^{i+1}={\lambda_w}^{i}-\alpha\times\frac{\partial}{\partial\lambda_w}CSMRIQ({\lambda_w}^{i},{\lambda_t}^{t})$$

$$\frac{\partial}{\partial\lambda_t}CSMRIQ({\lambda_w}^{i},{\lambda_t}^{t})=\frac{CSMRIQ({\lambda_t}^{i}+\Delta{\lambda_t}^{i})-CSMRIQ({\lambda_t}^{i})}{({\lambda_t}^{i}+\Delta{\lambda_t}^{i})-{\lambda_t}^{i}}~~~~~~~~~~~~~~~ \frac{\partial}{\partial\lambda_w}CSMRIQ({\lambda_w}^{i},{\lambda_t}^{t})=\frac{CSMRIQ({\lambda_w}^{i}+\Delta{\lambda_w}^{i})-CSMRIQ({\lambda_w}^{i})}{({\lambda_w}^{i}+\Delta{\lambda_w}^{i})-{\lambda_w}^{i}}$$

Results

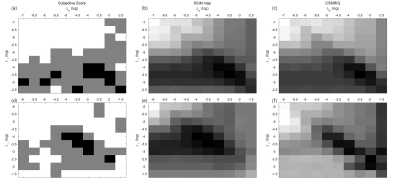
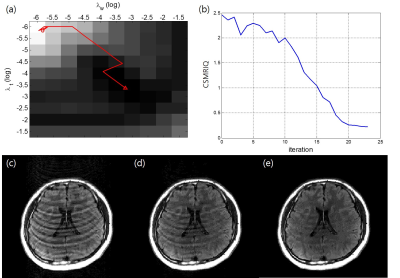
Figure 3 shows that CSMRIQ is highly correlated with subjective score of radiologist and SSIM. 100 images( combinations of 10 $$$\lambda_w$$$ and 10 $$$\lambda_t$$$ ) per subject is reconstructed and a radiologist evaluated one set. Correlations between CSMRIQ and subjective scoring is more than 0.8(both PLCC, SROCC). As well as subjective scoring, CSMRIQ has highly correlated with SSIM, the both SROCC and PLCC are over than 0.97 in 36 subjects t1-weighted, t2-weighted each. Figure 4 shows that optimizing the regularization parameters is successful. In optimizing regularization parameter experiment, we set initial parameters as $$$\lambda_w = 1.5\times10^{-6}$$$ , $$$\lambda_t = 1.5\times10^{-6}$$$ and maximum iteration number as 20. 71 subjects among 72 are successively optimized.

Conclusion

Choosing proper regularization parameters is very important in CS reconstruction in MRI. There are two conventional method to set regularization parameters; select empirically, L-curve method. Select parameters empirically cannot be reliable and also comparable. L-curve methods set more reliable result, but much time consuming. We proposed CSMRIQ which is no-reference image quality assessment for the CS reconstructed MR image so that evaluate and compare the CS reconstructed images. Furthermore, it can output the best CS image and its parameters automatically much faster than the L-curve method and it could be used in vivo.

Acknowledgements

This research was supported by the National Research Foundation of Korea (NRF) grant funded by the Korean government(MSIP) (2016R1A2R4015016).

References

[1] Lustig, Michael, David Donoho, and John M. Pauly. "Sparse MRI: The application of compressed sensing for rapid MR imaging." Magnetic resonance in medicine 58.6 (2007): 1182-1195.

[2] Hansen, Per Christian. The L-curve and its use in the numerical treatment of inverse problems. IMM, Department of Mathematical Modelling, Technical Universityof Denmark, 1999.

[3] Akasaka, Thai, et al. "Optimization of regularization parameters in compressed sensing of magnetic resonance angiography: Can statistical image metrics mimic radiologists' perception?." PloS one11.1 (2016): e0146548.

[4] Jinseong Jang, Bang et al. “QEMDIM : Quality Evaluation using Multi-DIrectional Filter for no-reference MR image”, 25th ISMRM 2017

[5] Kihun Bang, Jang et al. “Study on regularization paremeter tuning in compressed sensing using no-reference image quality assessment”, 25th ISMRM 2017

[6] Mittal, Anish, Rajiv Soundararajan, and Alan C. Bovik. "Making a “completely blind” image quality analyzer." IEEE Signal Processing Letters 20.3 (2013): 209-212.

[7] C. Jack, M. Bernstein, N. Fox, P. Thompson, G. Alexander, D. Harvey, B. Borowski, P. Britson, J. L. Whitwell, C. Ward, A. Dale, J. Felmlee, J. Gunter, D. Hill, R. Killiany, N. Schu, S. Fox-Bosetti, C. Lin, C. Studholme, C. DeCarli, Gunnar Krueger, H. Ward, G. Metzger, K. Scott, R. Mallozzi, D. Blezek, J. Levy, J. Debbins, A. Fleisher, M. Albert, R. Green, G. Bartzokis, G. Glover, J. Mugler and M. Weiner, "The Alzheimer's disease neuroimaging initiative (ADNI): MRI methods", J. Magn. Reson. Imaging, vol. 27, no. 4, pp. 685-691, 2008.

Figures

Figure 1. Process of CSMRIQ.

Figure 2. Process of optimizing regularization parameters.

Figure 3. Correlation of CSMRIQ with subjective score and SSIM. 100 images(combinations of 10 and 10 ) are reconstructed and evaluated by each metrics. (a),(d) is Subjective Score map evaluated by radiologist. (b),(d) is evaluated by SSIM and (c),(f) is evaluated by CSMRIQ. (a)-(c) is a map of T1-weighted images and (d)-(f) is a map of T2-weighted images.

Figure 4. Optimizing regularization parameters of T2-weighted image. (a) shows regularization parameters, (b) shows image quality of every steps. (c), (d), (e) is reconstructed image of 0th iteration, 15th iteration, 23th iteration each.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
2816