2813
L1, Lp, L2, and Elastic Net Penalties for Regularization of Two-Gaussian Component Distributions in One-dimensional Magnetic Resonance Relaxometry1Applied Mathematics & Statistics, and Scientific Computation (AMSC), University of Maryland, College Park, College Park, MD, United States, 2National Institute on Aging (NIA), Baltimore, MD, United States
Synopsis
Magnetic resonance (MR) relaxometry time distributions are recovered via the inverse Laplace transform (ILT), an ill-posed problem that is generally stabilized using Tikhonov regularization. Recent work has considered other penalties, such as the L1 penalty for locally narrow distributions. Lp penalties, 1<p<2, may be appropriate for distributions consisting of both narrow and broad components; a linear combination of L1 and L2 penalties, the elastic net (EN), may similarly be useful. However, there is little guidance regarding the choice of regularization penalty for the recovery of transverse relaxation distributions. We compare the effectiveness of each penalty for representative relaxation data.
PURPOSE
Magnetic resonance (MR) relaxometry is an emerging technique for characterizing biological tissues.1-3 Relaxation time distributions are recovered via the inverse Laplace transform (ILT), an ill-posed problem. This procedure is most often stabilized using Tikhonov regularization with an L2 penalty, defined as the sum of the squared elements of the solution vector. Recent advances in computational methods and interest in sparsity have motivated additional work evaluating other penalties. The promotion of sparsity by the L1 penalty is suitable for locally narrow transverse relaxation distributions.4 Lp penalties, 1<p<2, may be appropriate for distributions consisting of a combination of narrow and broad components; similarly, a linear combination of L1 and L2 penalties, the elastic net (EN), may be useful in such circumstances. However, there is little specific guidance regarding the choice of regularization penalty for the recovery of MR relaxation data. Here, we compare the effectiveness of each penalty for representative relaxation data.THEORY
The discrete measured signal takes the form
$$y(t_i)=\sum_{j=1}^KF(T_{2,j})e^{-t_i/T_{2,j}}$$
where $$$y(t_i)$$$ denotes signal amplitude at acquisition times $$$t_i$$$, typically integral multiples of an echo time (TE), $$$T_{2,j}$$$ denotes the decay time constant of the $$$j$$$th component, and $$$F(T_{2,j})$$$ is its associated magnitude. In matrix form:
$$y=AF$$
where
$$[A]_{i,j}=e^{-t_i/T_{2,j}},1\leq j\leq K$$
is the $$$n\times K$$$ kernal, $$$y$$$ is the length-$$$n$$$ vector representing measurements at time points $$$t_i,1\leq i\leq n$$$, and $$$F$$$ is a length-$$$K$$$ vector of amplitudes corresponding to possible relaxation times. With Tikhonov regularization, recovery of $$$F$$$ is cast as a nonnegatively constrained regularized least squares problem,
$$\min_{F\geq0}\{||AF-y||_2^2+\alpha^2||F ||_2^2\}$$
where $$$\alpha$$$ weights the regularization term relative to the fit residual. Similarly, for the L1 penalty, we have
$$\min_{F\geq0}\{||AF-y||_2^2+\alpha||F ||_1\}$$
while the Lp penalty appears as
$$\min_{F\geq0}\{||AF-y||_2^2+\alpha||F ||_p\}$$
and the EN penalty as
$$\min_{F\geq0}\{||AF-y||_2^2+\alpha_1||F ||_1+\alpha_2||F ||_2\}$$
METHODS
Our input model consists of a bimodal T2 distribution with Gaussian peaks, each characterized by mean T2 and standard deviation (SD). For Lp penalties, the regularization parameter was established within a range of [10-7,10-1]. For the EN penalty, a 5×5 grid search was performed across a range of [10-6,10-2] for α1 and a range of [10-7,10-3] for α2. Minimizations were performed using CVX software.5 The unknown model vector $$$F$$$ consisted of 176 allowable T2 rates, logarithmically spaced between 10 and 1000 ms. Noise-free decay data was generated at 352 discrete TE values, and then corrupted with additive white Gaussian noise, appropriate for spectroscopic or high signal-to-noise imaging experiments. Performance was evaluated using mean-squared error between the input model and the recovered distribution, normalized by the sum of the squared values of the input model.RESULTS
Figure 1 demonstrates the superiority of the L1 penalty in recovering a narrow distribution (Fig. 1a), and the superiority of the L2 penalty in recovering a wider-peak distribution (Fig. 1b). The heat maps in Figure 2a and 2b show performance across a range of models with varying (but equal in each peak) linewidths, and varying separations, for the L2 and L1 penalties, respectively. The L2 penalty is seen to perform well overall, but poorly for overlapping peaks. The L1 penalty clearly begins to fail as peak width increases, as expected. Figure 3 defines the optimal penalty across the same range of linewidths and peak separations. For a distribution of peaks of unequal SD, Figure 4 shows better performance by the L1.5 penalty as compared to the L2 penalty. Finally, Figure 5 demonstrates T2 distribution recovery for normal and osteoarthritic human cartilage samples,1 showing that all penalties recovered a bimodal distribution with roughly consistent peak centers but with markedly different peak SD. Based on our simulation analysis, we expect that the L1.5 recovery is likely to be the most appropriate.DISCUSSION
For sparse distributions, we find that the L1 penalty is optimal. The L2 penalty performs very well across a wide range of parameter values, underscoring the robustness of conventional Tikhonov regularization. Of particular interest are distributions with unequal peak widths, where neither the emphasis on sparsity from the L1 penalty nor the emphasis on smoothness in the L2 penalty are fully optimal. We found that the L1.5 and EN penalties were more successful in modeling this situation. Of these the elastic net promotes sparsity, but requires optimization over two regularization parameters, so that the L1.5 may be preferred overall. Overall, our results demonstrate the regions where the use of a particular regularization penalty term is likely to be most appropriate, and can be implemented in the usual case in which the experimentalist has a priori knowledge of the general characteristics of an underlying model distribution.Acknowledgements
This work was supported by the Intramural Research Program of the NIH, National Institute on Aging. We thank John Benedetto and Alfredo Nava-Tudela of the University of Maryland for their interest and comments. Tissue samples were kindly provided by Dr. Tariq A. Nayfeh.References
- Reiter DA, Irrechukwu O, Lin P-C, Moghadam S, Thaer SV, Pleshko N, et al. Improved MR-based characterization of engineered cartilage using multiexponential T2 relaxation and multivariate analysis. NMR in Biomedicine. 2012;25(3):476-88.
- Reiter DA, Roque RA, Lin P-C, Irrechukwu O, Doty S, Longo DL, et al. Mapping proteoglycan-bound water in cartilage: Improved specificity of matrix assessment using multiexponential transverse relaxation analysis. Magnetic Resonance in Medicine. 2010;65(2):377-84.
- Reiter DA, Lin P-C, Fishbein KW, Spencer RG. Multicomponent T2 relaxation analysis in cartilage. Magnetic Resonance in Medicine. 2009;61(4):803-9.
- Berman P, Levi O, Parmet Y, Saunders M, Wiesman Z. Laplace Inversion of Low-Resolution NMR Relaxometry Data Using Sparse Representation Methods. Concepts in Magnetic Resonance Part A. 2013;42A(3):72-88.
- Grant M, Boyd S. CVX: Matlab software for disciplined convex programming. 2.0 beta ed2013.
Figures
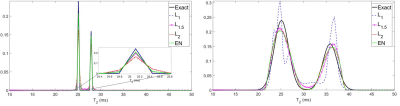
Figure 1a. (Left) Comparison of methods for recovery of two noiseless, closely-spaced, narrow Gaussian peaks, centered at 25 ms and 27.8 ms, with equal standard deviations of 0.1 ms. Note the superiority of the EN penalty over the L2 but not the L1 penalty, and similar performance of the L1.5 and EN penalties.
Figure 1b. (Right) Comparison of methods for recovery of two noiseless Gaussian peaks, wider than those of Figure 1a, centered at 25 ms and 35.9 ms, with equal standard deviations of 1.6 ms. Note the failure of the L1 penalty, and similar performance of the other penalties.
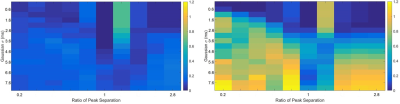
Figure 2. Average relative error over 20 trials, SNR 700, corresponding to peak width and peak separation for two Gaussian peaks of equal SD. The top leftmost square in the grids represents the relative error for the distribution with the most closely spaced and narrowest peaks. Moving right along the grids corresponds to changing the distance between the peaks, expressed as a ratio of peak centers along the T2 axis.
a. (Left) L2 penalty error. Note the general consistency of the recovery, best for well-separated, non-overlapping peaks.
b. (Right) L1 penalty error. Note the decrease in good recovery as peak
width increases.

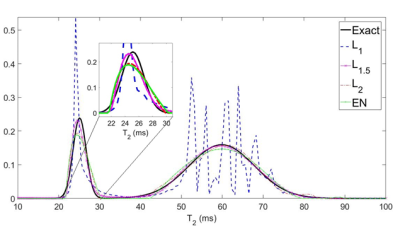
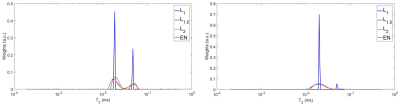
Figure 5. Magnetic resonance transverse relaxation time (T2) data for human cartilage explants taken from the tibial plateau.
a. (Left) This sample was obtained from an arthroplasty procedure and represents visually non-degraded tissue. Note the consistency of identified peak centers across all penalty terms.
b. (Right) This sample was obtained from the same arthroplasty procedure as in Fig. 5a, and represents visually degraded tissue. Comparing Fig. 5b with 5a, it is seen that the degraded tissue exhibits a larger average T2 value and a broader distribution as compared to the non-degraded sample. This indicates the extent of tissue breakdown within the osteoarthritic cartilage.