Synopsis

MRI is prone to noise pollution in imaging process.MRI with noise seriously affects the doctor's diagnosis of disease.In order to remove noise in MRI,this abstract considers a patch-based method that integrates Gaussian mixture models(GMMs) learning its parameters from external MRI patches with the clustering of desired patches guided by learned GMMs.The last step is to estimate the clear image by low-rank approximation process.Experimental results show the effectiveness of our method.Compared with the classical MRI denoising algorithm—NLM(Non Local Mean) and ADF(Anisotropic Diffusion Filter), our method achieves better results both visually and numerically.

Introduction

Clear Magnetic Resonance images (MRI) can benefit the doctor diagnosing the patient’s condition. Unfortunately, acquisitions of such clear MRI are challenging.Because of equipment defects or human’s operation error, it always makes MRI more or less noisy.So this abstract is aimed at MRI denoising.

In the field of natural images processing, there are so many denoising methods, which of them have a good denoising effect. Therefore, some methods initially proposed to tackle with natural images have been proposed to deal with MRI.

Denoising filter based on signal averaging principle may lead to blurred edge of image.So researchers proposed Anisotropic Diffusion filtering algorithm (ADF)to keep the edge of image^1,2.Using self similarity is also a good denoising method.The Non-Local Means denoising algorithm(NLM)³,which has been used in MRI denoising and whose performance is very desirable,takes full advantage of self similarity to denoise the image.In the abstract,we apply the method ⁴ initially proposed for natural images into the filed of MRI to denoise. We consider a patch-based method that integrates Gaussian mixture models(GMMs) learning its parameters from external clear MRI patches with the clustering of inner MRI patches (desired MRI patches)guided by learned GMMs. Finally,followed by a low-rank approximation process ,we estimate the clear image.

Method

Given a corrupted MRI y, we want to restore the latent clear MRI x.The image x can be estimated from y as follows:$$\left( {{\bf{\hat x}},\hat C,\left\{ {{{\hat Z}_k}} \right\}} \right) = \mathop {\arg \min }\limits_{x,C,\left\{ {{Z_k}} \right\}} \frac{\lambda }{{{\sigma ^2}}}\left\| {{\bf{y - x}}} \right\|_2^2 - \sum\limits_{i = 1}^m {\log p\left( {{R_i}{\bf{x}},{c_i}\left| \Theta \right.} \right)} + \sum\limits_{k = 1}^K {\left( {\frac{1}{{{\sigma ^2}}}\left\| {{{\bar R}_k}{\bf{x}} - {Z_k}} \right\|_F^2 + \tau {{\left\| {{Z_k}} \right\|}_ * }} \right)}$$where$$${R_i}{\bf{x}}(i = 1, \cdots m)$$$ represents the i-th image patch in image x.$$$K$$$stands for the number of Gauss models in the Gauss mixture model.$$$C$$$is class label.$$${c_i}$$$denotes$$${R_i}{\bf{x}}$$$ is from.$$${\bar R_k}{\bf{x}}$$$ denotes the matrix formed by the set of vectorized patches from the k-th class.$$$\lambda$$$ and $$$\tau$$$ are positive constant.$$$\sigma$$$ is noise standard deviation.$$$\Theta = \left( {{w_1},{w_2}, \cdots ,{w_K},{\theta _1},{\theta _2}, \cdots ,{\theta _K}} \right)$$$ is the set of GMMs parameters and$$$\sum\limits_{k = 1}^K {{w_k}} = 1$$$.Every $$${\theta _k}$$$ notes a Gaussian density function $$${p_k}$$$ parameterized by the mean $$${\mu _k}$$$ and covariance matrix $$${\Sigma _k}$$$.$$${Z_k}$$$denotes the low-rank matrix.$$$\left\| {{\bf{y - x}}} \right\|_2^2$$$ is fidelity term,$$$\sum\limits_{i = 1}^m {\log p\left( {{R_i}{\bf{x}},{c_i}\left| \Theta \right.} \right)}$$$ is patch clustering log likelihood term,$$$\sum\limits_{k = 1}^K {\left( {\frac{1}{{{\sigma ^2}}}\left\| {{{\bar R}_i}{\bf{x}} - {Z_k}} \right\|_F^2 + \tau {{\left\| {{Z_k}} \right\|}_ * }} \right)}$$$is low-rank regularization term.

As for patch cluster log likelihood term,it equals:$$\begin{array}{l}\log p\left( {{R_i}{\bf{x}},C\left| \Theta \right.} \right) = \sum\limits_{i = 1}^m {\log p\left( {{R_i}{\bf{x}},{c_i}\left| \Theta \right.} \right)} \\{\rm{ = }}\sum\limits_{i = 1}^m {\log p\left( {{R_i}{\bf{x}}\left| {{c_i},\Theta } \right.} \right)} p\left( {{c_i}} \right)\\{\rm{ = }}\sum\limits_{i = 1}^m {\log \left( {{w_{{c_i}}}{p_{{c_i}}}\left( {{R_i}{\bf{x}}\left| {{\theta _{{c_i}}}} \right.} \right)} \right)} {\rm{ = }}\sum\limits_{i = 1}^m {\log ({w_{{c_i}}} \cdot c \cdot \exp \left( { - \frac{1}{2}{{\left( {{R_i}{\bf{x}} - {\mu _{{c_i}}}} \right)}^T}\sum _{{c_i}}^{ - 1}\left( {{R_i}{\bf{x}} - {\mu _{{c_i}}}} \right)} \right)} \end{array}$$

where $$$c$$$ is normalization constant.

The optimal solution of Low-rank regularization term is based on SVD, and the specific method is given in the literature⁵.

Result

During the simulation experiment, all the experiment subjects come from Simulated Brain Database (SBD).Experiment subjects are generated using a powerful MR simulator.Experiment subjects plus noise is zero mean Gauss white noise. Image matrix size = 181× 217(Brain MRI)/ 256× 256(Bust MRI).

To get the GMMs,we learn the parameters with 250 mixture components from 2×10²⁶ patches.All patches sampled from 200 training MR images².Through experiment results ,we found setting different patch size for correspond standard deviation would get better performence.The involved parameters λ and γ in the method are fixed to 0.18 and 0.67.

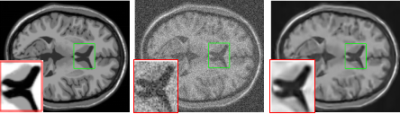
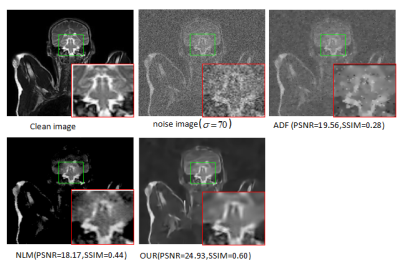
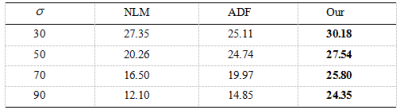
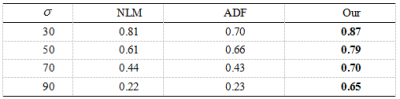
To validate the performance of our method , we compare it with NLM³ and ADF².The experimental image results are shown in Fig.1and Fig.2 . Denoising resultis compared with the original MRI image using the PSNR and the SSIM showed by Fig.3 and Fig.4, respectively.

Conclusion

Through the comparative experiments in different noise intensities and experiment with other denoising methods ,we can see our method applied in abstract outperforms NLM method and ADF method.The reason why our method can succeed in MRI denoising is that the method integrates external prior with internal clustering instead of with them separately.

However,with the increase of noise intensity,our method will make denoising image more smooth, resulting in serious loss of image detail information.Therefore,the further work is to analyze the reasons that make the image smoother and find out solutions to this problem , making our method improving the ability to denoise and retain detail in high noise conditions.

Acknowledgements

References

1.Gerig G, et al. Nonlinear anisotropic filtering of MRI data[J]. IEEE Transactions on medical imaging, 1992, 11(2): 221-232.

2.Samsonov A A, Johnson C R. Noise‐adaptive nonlinear diffusion filtering of MR images with spatially varying noise levels[J]. Magnetic Resonance in Medicine, 2004, 52(4): 798-806.

3.Manjón J V, et al. MRI denoising using non-local means[J]. Medical image analysis, 2008, 12(4): 514-523.

4.Chen F, Zhang L,Yu H.External patch prior guided internal clustering for image denoising[C]. In: Proceedings of the IEEE international conference on computer vision, 2015, 603-611.

5.S. Gu, L. Zhang, W. Zuo, and X. Feng. Weighted nuclearnorm minimization with application to image denoising.Proc. CVPR, 2014.