2810
Rapid acquisition for MSK applications using compressed sensing with small coils1Biomedical Imaging Center, Pontificia Universidad Católica de Chile, Santiago, Chile, 2Department of Electrical Engineering, Pontificia Universidad Católica de Chile, Santiago, Chile, 3Department of Orthopedics and Traumatology, School of Medicine, Pontificia Universidad Católica de Chile, Santiago, Chile, 4Department of Radiology, School of Medicine, Pontificia Universidad Católica de Chile, Santiago, Chile, 5Institute for Biological and Medical Engineering, Pontificia Universidad Católica de Chile, Santiago, Chile
Synopsis
There is a need for faster acquisitions of the MSK system. Particularly, for assessing the ACL at different degrees of flexion, and even better, for dynamic studies. Our work proposes how to obtain quasi-static images of the MSK, in particular for the study of the Anterior Cruciate Ligament (ACL), using smaller and less rigid coils by undersampling and compressed sensing reconstruction.
INTRODUCTION:
In the cardiac and brain systems, dynamic imaging techniques are well developed. However, that is not the case in the musculoskeletal system. In MSK, effective rapid imaging techniques have been introduced clinically using high factors of SENSE. Nevertheless, these coils are large and rigid and do not allow quasi-static or dynamic studies. Alternatively, small extremity coils allow the necessary flexibility for dynamic images. But, due to the position of the knee in the coil they lack sufficient signal to take full advantage of SENSE. Thus, we present an alternative to SENSE in small coils using compressed sensing6,7 (CS) which was validated for quasi-static flexion of the knee.METHODS:
Acquisition: 25 knee images in supine at various degrees of flexion served as our data. We used an eight channel small extremity coil in a 1.5T Philips scanner. We used a 3D T2W TSE sequence, 0.7 mm isotropic resolution and 156x156x22 mm FOV [TR 600ms; TE 60ms; 4:40s scan duration, fully sampled]. In one volunteer, we acquired two additional images with SENSE (100% and 50% of data). In this coil, a SENSE reconstruction with 25% of the data resulted in degraded images.
Reconstruction: Using CS, we reconstructed the 3D images using 20% of the sampled k-space. The under-sampling pattern acquired random samples in the in the $$$k_y$$$-$$$k_z$$$ plane, using a third-degree polynomial probability distribution with higher concentration in the center of k-space. We used the SPGL1 solver8,9 for the reconstruction with wavelet Daubechies DB4 as sparsifying transform.
Data: First, we tested the reconstruction algorithm and adjusted the CS parameters using a digital phantom created in k-space. Then, we applied the technique to knee images, retrospectively undersampling k-space. We measured and compared pixel intensity for the original and reconstructed images.
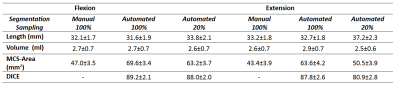
To validate the reconstruction, we segmented the ACL of the fully-sampled and 20% undersampled reconstructions. We used a fully-automated1,2,3 (FA) algorithm which was validated against manual segmentation elsewhere. For quality assessment of the reconstruction, we compared each ACL segmentation (via Length, Volume, and Medial Cross Sectional Area) against the fully sampled segmentation. We also show the DICE4 coefficient (intersection divided by the union of the two volumes) to check the FA segmentation.
RESULTS
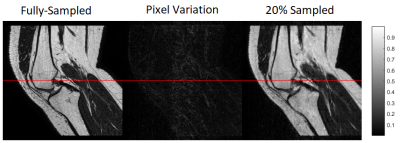
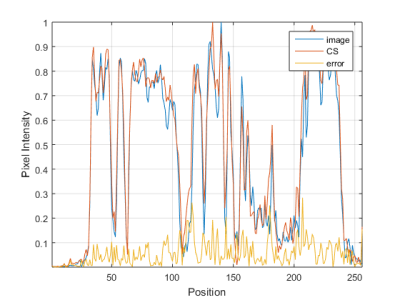
SENSE with 50% of data achieves a comparable segmentation to fully sampled, (with DICE factor of 91). The mean and standard deviation of the three measurements, for manual and fully automated segmentation with ACL in Flexion and Extension are listed in Table 1. In figure 1 we show an example of fully-sampled and 20% sampled reconstructions. In figure 2 we show the intensity values for the profile defied in figure 1. It can be appreciated that the CS reconstruction with only 20% of the data is closed to the fully sampled reconstruction. Certainly enough for segmenting the ACL.
DISCUSSION:
Our CS protocol with 20% sampling produces comparable images than the standard reconstruction with 100% sampling (DICE of 88.0±2.0 and 80.9±2.8 for Flexion and Extension respectively). This implies a reduction of acquisition time from 2:20 s (50% under-sampled) to 0:52 s (20% under-sampled). The ACL measurements for the under-sampled images are similar to that of the fully-sampled images. We expect that the MCS-Area measurement will improve with a larger database.CONCLUSION:
Our CS protocol is more rapid and precise than the equivalent SENSE protocol. Our research trajectory will continue to improve rapid imaging techniques to explore in vivo dynamic imaging of the ACL during knee flexion. A challenge moving forward will be increasing the width of FOV to capture the entirety of the intercondylar notch while maintaining rapid acquisition for semi-fluid imaging of the knee. In successive work, we are assessing the viability of combining CS and SENSE to achieve below 30 s permitting slow-motion capture of Flexion-Extension and Rotation in the knee. Such research has potential to reveal new physiological information improving the knowledge of the normal anatomy of the ACL. More broadly, these techniques can be applied for in vivo dynamic exploration of MSK systems beyond the knee.Acknowledgements
The first author supported by the Whitaker International Program and the study received funding from Anillo ACT1416.References
1. Mairal J, Bach F, Ponce J, Sapiro G. Online Learning for Matrix Factorization and Sparse Coding. Journal of Machine Learning Research, volume 11, pages 19-60. 2010.
2. Mairal J, Bach F, Ponce J, Sapiro G. Online Dictionary Learning for Sparse Coding. International Conference on Machine Learning, Montreal, Canada, 2009.
3. Tonga T, Wolza R, et al. Segmentation of MR images via Discriminative Dictionary Learning and Sparse Coding: Application to Hippocampus Labeling. Neuroimage. 2013 Aug 1;76:11-23.
4. Lee H, Hong H, and Kim J, Segmentation of anterior cruciate ligament in knee MR images using graph cuts with patient-specific shape constraints and label re fi nement, Comput. Biol. Med., vol. 55, pp. 1–10, 2014.
5. van den Berg E and Friedlander M. P., Probing the Pareto frontier for basis pursuit solutions, SIAM J. on Scientific Computing, 31(2):890-912, November 2008
6. Lustig, M., Donoho, D., & Pauly, J. M. (2007). Sparse MRI: The application of compressed sensing for rapid MR imaging. Magnetic Resonance in Medicine, 58(6), 1182–1195. http://doi.org/10.1002/mrm.21391
7. Lustig, M., Donoho, D. L., Santos, J. M., & Pauly, J. M. (2008). Compressed sensing MRI. IEEE Signal Processing Magazine, 25(March 2008), 72–82. http://doi.org/Doi 10.1109/Tit.2006.871582
8. E. van den Berg and M. P. Friedlander, Probing the Pareto frontier for basis pursuit solutions, SIAM J. on Scientific Computing, 31(2):890-912, November 2008
9. E. van den Berg and M. P. Friedlander, SPGL1: A solver for large-scale sparse reconstruction, http://www.cs.ubc.ca/labs/scl/spgl1, June, 2007