2809
Accelerating Non-Cartesian, Sparsity-Promoting Image Reconstruction Via Line Search FISTA1Center for Biomedical Imaging, New York University School of Medicine, New York, NY, United States, 2Electrical Engineering and Computer Science, University of Michigan, Ann Arbor, MI, United States
Synopsis
Iterative reconstruction algorithms for non-Cartesian MRI can have slow convergence due to the nonuniform density of k-space samples. Convergence speed can be improved by including the density compensation function into the algorithm, but current techniques for doing so can lead to SNR penalties or algorithm divergence. Here, we combine the use of density compensation with a line search under the MFISTA framework. The method has the convergence guarantees of MFISTA while gaining the speed improvements of using the density compensition function. The algorithm generalizes further to any FISTA algorithm.
Introduction
Iterative, non-Cartesian image reconstruction algorithms for sparsity-promoting regularization can have slow convergence due to the variation in the density of the k-space samples. A common solution is to include the density compensation function in the data fit term of the cost function, but this can lead to an SNR penalty in the reconstructed image.1 Alternative approaches include preconditioning2 or variable splitting,3 but these may require parameter tuning or they may not satisfy convergence conditions. Here we present an approach that is similar to a preconditioned FISTA4 with the modification of a line search routine on the data fidelity part of the cost function. We apply it to MOCHA,5 a state-of-the-art non-Cartesian MRI algorithm with weak convergence guarantees. The new approach has the convergence guarantees of MFISTA6 and the density compensation accelerations of MOCHA. It is also fully-automated and generalizes to any FISTA-type algorithm.Methods
Combining non-Cartesian trajectories with sparsity-promoting regularization can significantly accelerate MRI scans. To estimate images from these scans, we solve the following optimization problem:
$$\hat{x}=\underset{x}{argmin}\frac{1}{2}\left\|y-Ax\right\|_2^2+\beta\left\|Rx\right\|_1,$$
where $$$x$$$ is the image, $$$A$$$ is a non-Cartesian system matrix (with sensitivity coils), $$$y$$$ is the k-space data, and $$$R$$$ is a sparsifying transform. FISTA is a popular algorithm for such problems. Generally, FISTA-like algorithms solve at iteration $$$k$$$ the following problem:
$$x^{k+1}=\underset{x}{argmin}\frac{1}{2}\left\|x-b^k\right\|_{M_f}^2+\beta\left\|Rx\right\|_1,$$
where $$$M_f \succeq A'A$$$ is a majorizing matrix and $$$b^k=z^k-M_f^{-1}g^k$$$ comes from the data-fitting part. $$$g^k=A'(Az^k-y)$$$ is the data-fitting gradient at the shifted point $$$z^k=x^k+(t^k-1/t^{k+1})(x^k-x^{k-1})$$$. Typically, FISTA uses $$$M_f=LI$$$, where $$$L$$$ is the maximum eigenvalue of $$$A'A$$$, but other more general matrices are possible. Step sizes for the algorithm are related to $$$M_f^{-1}$$$. In some iterations - particularly early iterations - the $$$M_f^{-1}$$$ step size is conservative, and it is possible to take larger steps, which we will do using a line search. We propose to change the gradient step to
$$b^{k}=z^k-\alpha^kM_f^{-1}g^k,$$
where
$$\alpha^k=\frac{\text{real}\left \{\left< M_f^{-1}g^k,g^k\right >\right \}}{\left\|AM_f^{-1}g^k\right\|_2^2}.$$
This is equivalent to applying a steepest descent line search routine to the $$$M_f^{-1}g^k$$$ search direction for the data-fitting part of the cost function. The denoising subproblem shown above that incorporates the properties of the regularizer can also be accelerated based on $$$\alpha$$$.5 Applying this line search can allow the algorithm to take a larger or smaller step, depending on the iteration. We can guarantee convergence of the proposed method by evaluating the cost function at $$$x^k$$$ and guaranteeing monotonicity as in MFISTA.6 This can be accomplished with minimal computation by storing a few extra variables in memory.7
We applied the new line search procedure to non-Cartesian image reconstruction with a MOCHA approximate majorizer.5 The MOCHA procedure builds a circulant $$$M_f$$$ that is designed to mimic the properties of the density compensation function to speed convergence, but it does not guarantee the FISTA condition of $$$M_f \succeq A'A$$$. The line search helps the algorithm take smaller steps in cases where $$$M_f \succeq A'A$$$ is not satisfied, and we can also guarantee convergence due to the MFISTA cost function checks.
We applied the new algorithm to a 50-spoke radial brain MRI data set with 4 sensitivity coils.8
Results
We tested three algorithms in our numerical experiments. FISTA4,6 used $$$M_f=LI$$$, where $$$L$$$ is the Lipschitz constant. MOCHA5 used a circulant $$$M_f$$$ designed to emulate the density compensation function. LS-MOCHA is the standard MOCHA with the proposed line search improvements.
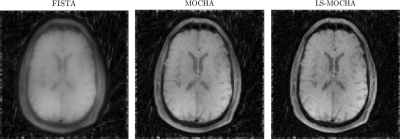
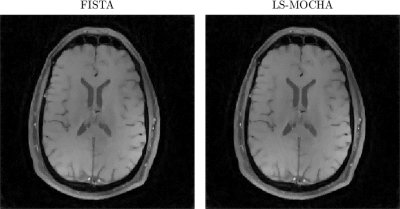
Figure 1 shows the images after 5 iterations of each algorithm. FISTA is further from convergence because it doesn't incorporate the k-space sampling density, while MOCHA and LS-MOCHA are closer to convergence due to the circulant majorizer. Figure 2 shows images after 150 iterations of each algorithm. By this point FISTA and LS-MOCHA are qualitatively similar. We do not show MOCHA since MOCHA diverged before reaching this point. Figure 3 shows a convergence plot of the normalized residual,
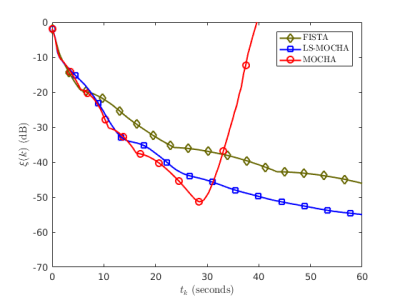
$$\xi(k)=\frac{\left \|x^k-x^{\infty}\right \|}{\left \|x^{\infty}\right \|},$$
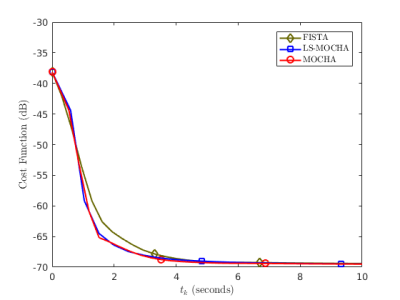
where $$$x^{\infty}$$$ is estimated by running many thousands of iterations of FISTA. After 20 seconds, MOCHA diverges since it failed to design $$$M_f$$$ such that $$$M_f \succeq A'A$$$ for this data set. LS-MOCHA is the fastest method. The results in Figure 3 are confirmed by cost function plots in Figure 4.
Conclusion
We have developed a new line search method that accelerates FISTA-type algorithms. We demonstrated that the new method can both accelerate and improve the robustness of non-Cartesian compressed sensing reconstruction. The method is generalizable to any FISTA-type algorithm. We chose to use a line search to determine $$$\alpha^k$$$, but in the future we plan to investigate other choices for $$$\alpha^k$$$, as well as new applications such as dynamic imaging.Acknowledgements
We would like to thank K. T. Block et al. for publishing the data used in this abstract.
The authors would like to thank A. R. De Pierro and G. T. Herman for discussions on line search methods.
The authors would also like to thank NIH R01 EB023618 and NIH U01 EB018760 for funding that supported this work.
References
1. B. P. Sutton, D. C. Noll, & J.A. Fessler. "Fast, iterative image reconstruction for MRI in the presence of field inhomogeneities," IEEE Trans. Med. Imag., vol. 22, pp. 178-188, 2003.
2. B. Mailhe, Q. Wang, R. Grimm, M. D. Nickel, K. T. Block, H. Chandarana, and M. S. Nadar. "Density compensation for iterative reconstruction from under-sampled radial data," in Proc. Int. Soc. Magn. Res. Med., 2015.
3. S. Ramani & J. A. Fessler. "Parallel MR image reconstruction using augmented Lagrangian methods," IEEE Trans. Med. Imag., vol. 30, pp. 694-706, 2011.
4. A. Beck & M. Teboulle. "A fast iterative shrinkage-thresholding algorithm for linear inverse problems," SIAM Jour. Imag. Sci., vol. 2, pp. 183-202, 2009.
5. M. J. Muckley, D. C. Noll, and J. A. Fessler, “Fast, iterative subsampled spiral reconstruction via circulant majorizers,” in Proc. Int. Soc. Magn. Res. Med., 2016.
6. A. Beck & M. Teboulle. "Fast gradient-based algorithms for constrained total variation image denoising and deblurring problems," IEEE Trans. Imag. Proc., vol. 18, pp. 2419-2434, 2009.
7. M. V. Zibetti, E. S. Helou, & D. R. Pipa. "Accelerating Overrelaxed and Monotone Fast Iterative Shrinkage-Thresholding Algorithms With Line Search for Sparse Reconstructions," IEEE Trans. Imag. Proc., vol. 26, pp. 3569-3578, 2017.
8. K. T. Block, M. Uecker, & J. Frahm. "Undersampled radial MRI with multiple coils. Iterative image reconstruction using a total variation constraint," Magn. Res. Med., vol. 57, pp. 1086-1098, 2007.
Figures