2808

Parameter-free Parallel Imaging and Compressed Sensing
Jonathan I Tamir1, Frank Ong1, Shreyas S Vasanawala2, and Michael Lustig1

1Electrical Engineering and Computer Sciences, University of California, Berkeley, Berkeley, CA, United States, 2Radiology, Stanford University, Stanford, CA, United States

Synopsis

We demonstrate an end-to-end parallel imaging and compressed sensing reconstruction that does not rely on parameter tuning. We combine noise pre-whitening, auto-tuned coil sensitivity estimation, and a noise-constrained compressed sensing reconstruction to eliminate the need to select parameters such as soft threshold regularization. The method is validated across a large corpus of phantom and in vivo data at different levels of SNR and with different types of coils in 2D and in 3D. An end-to-end reconstruction is shown for 2D variable density single-shot fast spin-echo with reconstruction times of less than one minute.

Introduction

Parallel-imaging (PI) [1] and compressed-sensing (CS) [2], herein called PICS, have shown great promise at accelerating MRI. Many techniques build off of PICS to exploit redundant structure, and the success of CS has begun to penetrate the clinic [3]. Nonetheless, broader clinical use of CS is hindered by the need to carefully tune regularization parameters. Although sensitivity to these parameters may be mild in some cases, in others it can lead to noise amplification or over-smoothing due to differences in SNR, acquisition, slice, or anatomy. Coil sensitivity estimation may pose an additional challenge, as it may also depend on algorithm parameters that are sensitive to differences across scans.

In this work we implement an end-to-end PICS reconstruction that does not rely on parameter tuning. This is accomplished by (1) pre-whitening the acquired data using a noise pre-scan, (2) performing an auto-tuned and auto-calibrated coil sensitivity estimation [4,5], and (3) using a noise-constrained CS formulation [6]. The method is validated on both phantom and in vivo data at different SNRs and with different types of coils in 2D and in 3D. An end-to-end reconstruction is shown for 2D variable density single-shot fast spin-echo (VD-SSFSE) with reconstruction times under one minute.

Theory

When the noise level is known, PICS can be formulated as basis pursuit denoising [6]:$$\begin{aligned}&\underset{\mathbf{x}}{\text{minimize}}&&||\mathbf{Wx}||_1\\&\text{subject to}&&||\mathbf{y}-\mathbf{Ax}||_2\le\sigma\sqrt{n},\end{aligned}$$where $$$\mathbf x$$$ is the unknown image, $$$\mathbf W$$$ is a sparsity transform (wavelets for this work), $$$\mathbf A$$$ is the forward model incorporating estimated coil sensitivities, $$$\mathbf y\in\mathbb{R}^n$$$ are the k-space measurements, and $$$\sigma$$$ is the noise standard deviation. The l1-norm of the wavelet coefficients is minimized subject to a data inconsistency at most equal to the expected value of the noise in the acquisition. This problem can be efficiently solved with gradient-based methods, e.g. ADMM [7] and first-order primal-dual algorithm [8]. Since the noise level is known, the coil sensitivities can be reliably estimated using an auto-tuned [5] variant of ESPIRiT [6], an auto-calibration PI method.

Methods

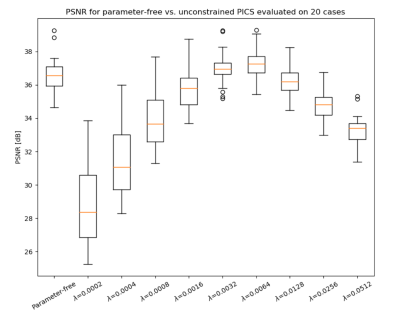
Three experiments were performed. In the first, twenty fully sampled 3D fast spin-echo (FSE) knee datasets acquired at 3T were downloaded from http://www.mridata.org [9]. For each, nine central slices were averaged to serve as noise-free ground truth. After, noise was added to each averaged slice and the data were retrospectively under-sampled using a Poisson-disc sampling pattern (R=4). Each case was reconstructed with parameter-free PICS using the first-order primal-dual algorithm, as well as unconstrained PICS using FISTA [10] at different levels of regularization. The PSNR was evaluated and compared across the 20 cases.

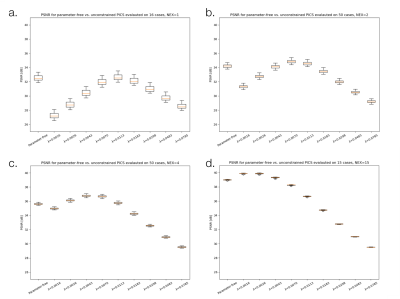
In the second experiment, a fully sampled slice of the NIST/ISMRM System Phantom was acquired at 3T with a 32 channel body coil using 2D FSE, and the acquisition was repeated 16 times. A noise pre-scan was used to pre-whiten the data to unit variance. Different SNR levels were achieved by averaging an appropriate number of acquisitions, followed by retrospective Poisson-disc under-sampling (R=4) and coil compression to 16 channels [11]. Each case was reconstructed with parameter-free PICS and unconstrained PICS with different regularization parameters. The PSNR was evaluated and compared across different instances of averaged acquisitions.In the third experiment, an adult patient's abdomen was scanned with 2D prospectively under-sampled VD-SSFSE [12] at 3T with IRB approval and informed consent. The data were pre-whitened using a noise pre-scan, coil sensitivities were estimated with auto-tuned ESPIRiT, and the data were reconstructed using parameter-free and unconstrained PICS. As a proof-of-principle, an end-to-end reconstruction based on the acquisition was developed and integrated into the Stanford Hospital. The reconstructions were implemented and merged into the Berkeley Advanced Reconstruction Toolbox [13,14].

Results

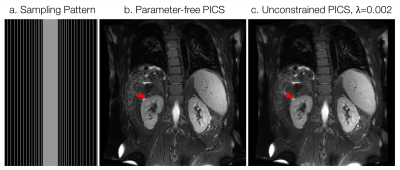
Fig.1 shows a fully sampled knee compared to parameter-free and unconstrained PICS for different regularization parameters. Fig.2 shows a box-plot of the PSNR across the 20 cases for noise $$$\sigma=0.0128$$$. The fluctuation in PSNR for parameter-free PICS across the 20 cases is low and the PSNR is comparable to a manually tuned, unconstrained PICS reconstruction. Fig.3 shows the phantom data for several signal averages, and reconstructions with parameter-free PICS and unconstrained PICS with $$$\lambda=0.007$$$. Fig.4 shows box plots of PSNRs for the phantom for different numbers of signal averages. The phantom data show a similar trend to that of the knee data. Fig.5 shows the sampling pattern for the VD-SSFSE data, and the parameter-free and unconstrained reconstructions in a central slice of the abdomen. The unconstrained reconstruction used a previously tuned regularization parameter of $$$\lambda=0.002$$$ [12]. There is improved visualization of structure in the kidney. The end-to-end reconstruction time was 43 seconds for 40 slices on a 24-core Xeon E5-2670 machine.

Acknowledgements

We thank GE Healthcare for help with the noise pre-whitening and Valentina Taviani for providing the VS-SSFSE data.

References

  1. KP Pruessmann, M Weiger, MB Scheidegger, P Boesiger. "SENSE: Sensitivity Encoding for Fast MRI." Magnetic resonance in medicine 42, no. 5 (1999): 952-62
  2. M Lustig, D Donoho, JM Pauly. "Sparse MRI: The Application of Compressed Sensing for Rapid MR Imaging." Magnetic resonance in medicine 58, no. 6 (2007): doi:10.1002/mrm.21391.
  3. SS Vasanawala, MT Alley, BA Hargreaves, RA Barth, JM Pauly, M Lustig. "Improved Pediatric MR Imaging with Compressed Sensing." Radiology 256, no. 2 (2010): doi:10.1148/radiol.10091218.
  4. M Uecker, P Lai, MJ Murphy, P Virtue, M Elad, JM Pauly, SS Vasanawala, M Lustig. "ESPIRiT-an Eigenvalue Approach to Autocalibrating Parallel MRI: Where SENSE Meets GRAPPA." Magnetic resonance in medicine 71, no. 3 (2014): doi:10.1002/mrm.24751.
  5. SS Iyer, F Ong, M Lustig. Towards a Parameter Free ESPIRiT: Soft Weighting for Robust Coil Sensitivity Estimation. ISMRM 24th Annual Meeting, Singapore 2016.
  6. S Chen, D Donoho. Basis Pursuit. Technical Report, Department of Statistics, Stanford University.
  7. S Boyd, N Parikh, E Chu, B Peleato, J Eckstein. "Distributed Optimization and Statistical Learning Via the Alternating Direction Method of Multipliers." Foundations and Trends in Machine Learning 3, no. 1 (2011): 1-122.
  8. A Chambolle, T Pock. "A First-order Primal-dual Algorithm for Convex Problems with Applications to Imaging." Journal of Mathematical Imaging and Vision 40, no. 1 (2011): 120-145.
  9. K Epperson, AM Sawyer, M Lustig, M Alley, M Uecker, P Virtue, P Lai, SS Vasanawala. Creation of Fully Sampled MR Data Repository for Compressed Sensing of the Knee. SMRT 22nd Annual Meeting, Salt Lake City 2013.
  10. A Beck, M Teboulle. "A Fast Iterative Shrinkage-Thresholding Algorithm for Linear Inverse Problems." SIAM Journal on Imaging Sciences 2, no. 1 (2009): doi:10.1137/080716542.
  11. F Huang S Vijayakumar, Y Li, S Hertel, GR Duensing. A software channel compression technique for faster reconstruction with many channels. Magn Reson Imaging 2008;26:133-141.
  12. V Taviani, DV Litwiller, JI Tamir, AM Loening, BA Hargreaves, SS Vasanawala. Variable density compressed sensing single shot fast spin echo. In: Proc 24th Annual Meeting ISMRM, Singapore; 2016. p 618.
  13. M Uecker, JI Tamir; F Ong; C Holme M Lustig, BART: version 0.4. DOI: 10.5281/zenodo.817472.
  14. M Uecker, F Ong, JI Tamir, D Bahri, P Virtue, JY Cheng, T Zhang, M Lustig. Berkeley Advanced Reconstruction Toolbox, Annual Meeting ISMRM, Toronto 2015, In Proc. Intl. Soc. Mag. Reson. Med 23; 2486 (2015)

Figures

Comparison of (b) parameter-free constrained PICS to (c-f) unconstrained PICS with different regularization parameters. Nine central slices of a fully sampled 3D FSE knee MRI were used as a ground truth image (a). The ground truth data were retrospectively corrupted with noise ($$$\sigma=0.0128$$$) and under-sampled with variable density Poisson disc sampling (R=4). The constrained PICS reconstruction matches the quality of the unconstrained PICS reconstruction at a regularization parameter of $$$\lambda=0.001$$$.

Box-plot comparing PSNRs for parameter-free vs. unconstrained PICS reconstructions across all 20 knee MRI cases. The parameter-free reconstruction achieves near-equal PSNR compared to the unconstrained reconstruction with the best-choice regularization parameter.

Comparison of fully sampled NIST/ISMRM system phantom with different number of signal averages (NEX) to retrospectively under-sampled (R=4) reconstructions with parameter-free and unconstrained PICS ($$$\lambda=0.007$$$). The parameter-free reconstructions remain consistent across SNR levels.

Box-plots comparing PSNRs for parameter-free vs. unconstrained PICS reconstructions for (a) NEX=1, (b) NEX=2, (c) NEX=4, (d) NEX=15 on the NIST/ISMRM phantom. The best regularization parameter for the unconstrained reconstruction depends on the SNR level. The parameter-free reconstruction achieves a nice balance between optimal PSNR and robustness.

(a) Sampling pattern and comparison of (b) parameter-free vs (c) unconstrained PICS reconstruction on prospectively under-sampled variable density single-shot fast spin-echo (VD-SSFSE) scan of an adult abdomen. The unconstrained reconstruction used the default regularization parameter of , which was fixed when the protocol was designed. The parameter-free reconstruction shows improved detail in the kidneys (red arrow).

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
2808