Synopsis

Magnetic resonance image (MRI) super-resolution (SR) algorithms have been applied to increase the spatial resolution of scans after acquisition, thus facilitating the clinical diagnosis. Motivated by the great success of deep convolutional neural network in computer vision, we introduced an Enhanced Recursive Residual Network (ERRN) for MRI SR. We show that the performance of our method exceeds conventional learning based methods (sparse coding-based ScSR, CNN-based SRCNN and VDSR) in terms of reconstruction error, peak-signal-to-noise-ratio (PSNR) and structure similarity index (SSIM) value.

Purpose

SR technology is essential in MRI where high quality images are not prone to acquire due to acquisition constraint. The aim of this work is to enhance MRI resolution using a deep CNN network.

Method

Without loss of generality, the MRI acquisition model can be formulated as an ill-posed inverse problem:$$\mathbf{\mathit{y}}=\mathbf{\mathit{DH}}x +\mathbf{\mathit{v}}$$where $$$H$$$ and $$$ D$$$ depict the blurring and down-sampling effects respectively. In order to relieve ill-posedness of this inversion, optimization methods can be employed to find the best approximate high-resolution (HR) image. In this work, we apply a deep convolutional neural network named Enhanced Recursive Residual Network (ERRN) to learn an inference function with stochastic gradient descent serving as the optimization process:$$\min_{\Theta }loss\left ( \hat{x},x \right ),s.t.\hat{x}= \mathcal{F}\left ( y,D,H;\Theta \right )$$where $$$\mathcal{F}\left ( \cdot \right )$$$ is the inference function (deep convolutional neural network) with parameter set $$$\Theta $$$, and $$$loss\left ( \cdot \right )$$$is the loss function measuring the similarity between output SR $$$\hat{x}$$$ and ground-truth HR $$$x$$$.

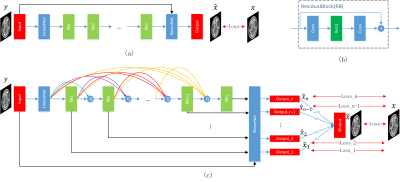
We first introduce a basic model of recursive residual network and then an enhanced network with densely-connection and multi-supervision. An overview of our basic model(ERRN_Basic) for MRI SR is provided in Fig.1(a), mainly consisting of three parts: the embedding network, inference network and reconstruction network. Specifically, a convolutional layer is used in the embedding network to extract the features from the input LR image. The inference network is stacked by $$$n$$$ recursive residual blocks. Ultimately, outputs of final residual block are reconstructed by the reconstruction layer.

Since residual network¹ has exhibited excellent performance in deep learning, we use $$$n$$$ residual blocks as illustrated in Fig.1(b) stacked to serve as inference network. To ease the training as well as control the model parameters while increasing the depth, recursive learning is adopted in the same residual blocks. Moreover, the feature maps of each residual block are propagated into all subsequent residual blocks, providing an efficient densely-connected way to combine different level features. At the same time, a gate unit is adopted to achieve an adaptive learning policy, which automatically decides the importance of the feature maps obtained from previous residual blocks. In the end, to further explore the feature from low level to high level, we send the outputs of different residual blocks to the same reconstruction net getting intermediate predictions, and the ultimate output can be computed via adaptive weighted averaging. All the $$$n$$$ intermediate outputs $$$\hat{x}_{1},\hat{x}_{2},...,\hat{x}_{n-1},\hat{x}_{n}$$$ and the final output $$$\hat{x}$$$ are supervised simultaneously during training. The final ERRN with densely-connection and multi-supervision is showed in Fig.1(c).

Result and Discussion

In our network, the number $$$n$$$ of residual blocks is set to be 10. The training dataset contains 270 MPRAGE brain images of size $$$256\times 256$$$ in the experiment. HR and LR counterparts are split into $$$31\times 31$$$ patches to construct the training pairs $$$ \left \{ \left ( x_{l},y_{l} \right ) \right \}_{l=1}^{L}$$$.

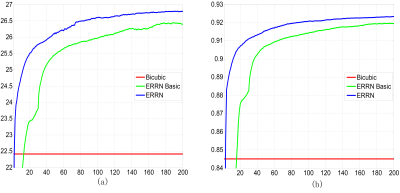
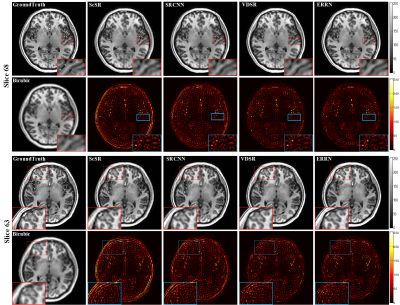
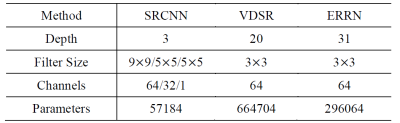
We first compare the test convergence curves of the ERRN network and the basic model in terms of PSNR and SSIM in Fig.2. We observe that the ERRN performs better with densely-connection and multi-supervision than the basic model. We compare our ERRN method with several state-of-the-art methods: sparse coding-based SR method ScSR², a shallow CNN-based SR method SRCNN³ with 3 layers convolutional network and a deep CNN-based SR method VDSR⁴ with 20 layers. The visual results on two example slices are presented in Fig.3, showing our ERRN method can recover more accurate tissue structure. The SR results of different methods are evaluated by PSNR and SSIM with 10 MR images in the test dataset in Table1, where our ERRN method achieves the best performance on both scales of 3 and 4. Table 2 presents the network architectures. Compared with SRCNN³, we find that deeper networks, such as VDSR⁴ with 20 layers and our 31-layers ERRN network, indeed boost the MRI reconstruction performance. Since recursive learning is adopted, we trained a deeper ERRN network with less parameters than VDSR⁴, but higher PSNR.

Conclusion

Acknowledgements

References

1. He K, Zhang X, Ren S, et al. Deep residual learning for image recognition. Proceedings of the IEEE conference on computer vision and pattern recognition. 2016: 770-778.

2. Yang J, Wright J, Huang T S, et al. Image super-resolution via sparse representation. IEEE transactions on image processing, 2010, 19(11): 2861-73.

3. Dong C, Loy C C, He K, et al. Image super-resolution using deep convolutional networks. IEEE transactions on pattern analysis and machine intelligence, 2016, 38(2): 295-307.

4. Kim J, Kwon Lee J, Mu Lee K. Accurate image super-resolution using very deep convolutional networks. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2016: 1646-1654.