2799
Deep Sinogram Learning for Radial MRI: Comparison with k-space and Image Learning1Yonsei University, Seoul, Republic of Korea, 2Philips Korea, Seoul, Republic of Korea
Synopsis
Deep Sinogram Learning for Radial MRI: Comparison with k-space- and image learning. We demonstrated that singoram learning was more effective than k-space- or image learning in terms of restoring tissue structures and removal of streaking artifacts while not making those as real structures.
Introduction
Radial Magnetic Resonance Imaging (MRI), which encodes k-space along radial spokes instead of parallel rows, has been increasingly used in dynamic imaging and fast imaging owing to its robustness for motion [1, 2]. In addition, to increase spatial/temporal resolution or acquire more contrast images within the same scan time, image reconstruction methods such as compressed sensing (CS) which reconstruct images with a small number of spokes have been introduced for radial MRI [1,3]. Meanwhile, in recent, deep convolutional neural networks (CNNs)-based reconstruction methods showed superior performance than conventional methods [4]. In this study, we propose a deep CNN that estimates an image from radial undersampled data. On the basis of Fourier-slice theorem, radial k-space can be transformed to sinogram, which is identical to radon transform of the image to be reconstructed. Considering this point, we developed a deep CNN-based method operating on a sinogram obtained by 1D IFT of radial k-space, and compared its performance with deep CNNs operating on other two domains, k-space and image domain.Methods
For training and testing, we used T2-fluid attenuated inversion recovery (T2-FLAIR) brain dataset provided by the Alzheimer's Disease Neuroimaging Initiative (ADNI) [5]. A total number of 450 images were used for training and 50 images were used for testing. For training and testing dataset, we obtain full and undersampled radial data by inverse gridding 2D Cartesian data. Details of the CNN used in this study as follow: The network depths=25, filter size=3×3, the number of feature maps=64, activation function is leaky rectified linear unit (ReLU), optimizer is mini-batch SGD with momentum=0.9, weight decay=0.0001, the batch size=50. It took an average of 2.5 s to reconstruct a single 256×256 image using the MatConvNet library [6].
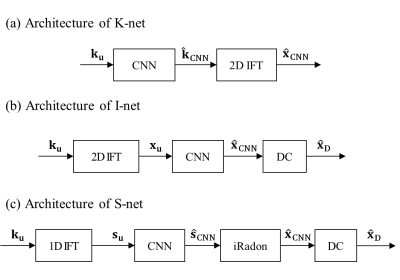
We tested three reconstruction frameworks based on deep CNNs for radial k-space data. Fig. 1 shows the architectures of K-net, I-net, and S-net, which are based on CNNs operating on the three different domains, k-space, image, and sinogram, respectively. In K-net (Fig.1(a)), the radial undersampled data, $$${k}_{u}$$$, passes through CNN to give the estimation $$$\hat{k}_{CNN}$$$. Then the output image, $$$\hat{x}_{CNN}$$$, is obtained as 2D IFT of $$$\hat{k}_{CNN}$$$. I-net comprises three components: gridding, CNN, and data consistency (DC) (Fig.1 (b)). $$${k}_{u}$$$ is gridded, and $$${x}_{u}$$$, which is the 2D IFT of Cartesian k-space, is obtained. It passes through CNN to give $$$\hat{x}_{CNN}$$$, and data consistency is performed by filling acquired k-space to k-space of $$$\hat{x}_{CNN}$$$. Then, IFT of the k-space with data consistency gives final output image, $$$\hat{x}_{D}$$$. in Fig.1(c), the architecture of the proposed S-net is shown; namely, 1D IFT, CNN, inverse Radon transform, and DC. 1D IFT of $$${k}_{u}$$$ gives the undersampled sinogram, $$${s}_{u}$$$. $$${s}_{u}$$$ passes through CNN to give $$$\hat{s}_{CNN}$$$. It is inverse radon transformed to give $$$\hat{x}_{CNN}$$$, and data consistency is performed to $$$\hat{x}_{CNN}$$$ to give the final output image $$$\hat{x}_{D}$$$.
Results
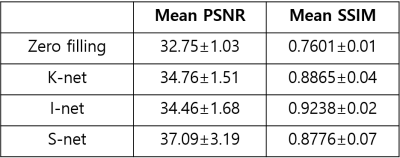
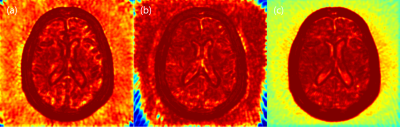
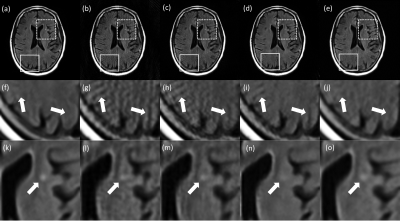
Table.1 shows the mean PSNR and SSIM scores of test images. The PSNR score is highest in the S-net, but the SSIM score is highest in the I-net. As shown in Fig.2, S-net has lower SSIM score than I-net because of low SSIM score of background. In the Brain region, I-net and S-net have similar SSIM values. Fig.3 shows images reconstructed with 64 spokes. K-net images still have some streaking artifacts. In I-net, the effect of artifacts caused new structures that did not originally exist (white arrows in Fig.3). S-net removed the streaking artifacts well while preserving the original structure information, resulting in better performance than the other methods.Discussion
Image vs. sinogram learning
Image learning has two problems to be solved simultaneously: 1) removal of streaking artifacts and 2) restoration of distorted tissue structures due to undersampling. Therefore, I-net can make the artifacts more sharper and to more realistic structures once it mistakes the high-frequency streaking artifacts on images as real structures. On the other hand, sinogram learning can be regarded as one interpolation problem that predicts unacquired sinogram samples using non-distorted acquired samples.
k-space vs. sinogram learning
k-space learning, which estimates unacquired k-space samples using acquired k-space samples, is an interpolation problem as sinogram learning. However, because k-space has less structural patterns than sinogram, CNNs which recognize structural information using various filters may be less efficient for k-space than sinogram.
Conclusion
We developed a CNN-based reconstruction method operating on sinogram for radial MRI and compared it with k-space- and image learning. Singoram learning was more effective than k-space- or image learning in terms of restoring tissue structures and removal of streaking artifacts while not making those as real structures.Acknowledgements
National Research Foundation of Korea (NRF) grant funded by the Korean government(MSIP) (2016R1A2R4015016).References
[1] Feng, Li, et al. "XD‐GRASP: Golden‐angle radial MRI with reconstruction of extra motion‐state dimensions using compressed sensing." Magnetic resonance in medicine 75.2 (2016): 775-788.
[2] Johnson, Kevin M., et al. "Optimized 3D ultrashort echo time pulmonary MRI." Magnetic resonance in medicine 70.5 (2013): 1241-1250.
[3] Feng, Li, et al. "Golden‐angle radial sparse parallel MRI: Combination of compressed sensing, parallel imaging, and golden‐angle radial sampling for fast and flexible dynamic volumetric MRI." Magnetic resonance in medicine 72.3 (2014): 707-717.
[4] Wang, Shanshan, et al. "Accelerating magnetic resonance imaging via deep learning." Biomedical Imaging (ISBI), 2016 IEEE 13th International Symposium on. IEEE, 2016.
[5] Jack, Clifford R., et al. "The Alzheimer's disease neuroimaging initiative (ADNI): MRI methods." Journal of magnetic resonance imaging 27.4 (2008): 685-691.
[6] Vedaldi, Andrea, and Karel Lenc. "Matconvnet: Convolutional neural networks for matlab." Proceedings of the 23rd ACM international conference on Multimedia. ACM, 2015.
Figures