2797
Noise Level Adaptive Deep Convolutional Neural Network for Image Denoising1Corporate research and development center, Toshiba corporation, Kawasaki, Japan, 2MRI system division, Toshiba Medical Systems Corporation, Otawara, Japan, 3MRI Systems Development Department, Toshiba Medical Systems Corporation, Otawara, Japan
Synopsis
For integrated diagnosis, MRI provides various types of images related to different acquisition parameters. The change of the acquisition parameters affects noise levels of the provided image in meaningful ways. To adapt the change of the noise level, it is desirable for denoising methods to be adaptive to the noise level, but deep neural network methods are not adaptive, despite their high performance. We propose a deep convolutional neural network (CNN) adjustable to noise levels. The activation functions of the CNN use soft shrinkage whose threshold is proportional to noise level of the input image.
Introduction
Denoising methods based on deep CNN have recently achieved high image quality. However they impose larger computational cost for training, under the condition that noise levels of the input images range widely.These methods employ noisy-clean image pairs to train a CNN, and the trained CNN efficiently reduces noises whose level is near to that of the noisy images used in training. But the larger the difference between the noise level of input and that of images used in training, the worse the quality of the denoised image becomes. Therefore, we need to train more than one CNN, with each CNN separately related to a different noise level, and select one of the CNNs according to the noise level of the input image. If the number of CNNs increases, computational cost for training also increases.
Contrary to that, existing noise reduction methods are applied to various types of images individually, because their parameters can be adjusted to various noise levels of input. The noise level can be estimated from the acquisition parameters and so on.
Therefore, to reduce various noises by using one CNN, we propose a deep CNN using an activation function whose parameter is adjustable to noise.
Methods
The proposed network architecture is based on DnCNN1 shown in Fig. 1. In the feature extraction layer, the convolution and the activation function are applied to the input noisy image. Next, the convolution, the batch normalization and activation function are repeated as the feature conversion layer. Finally, the residual image is generated from the convolution in the residual image generation layer, and added to the input image for the output denoised image.
Whereas the Rectified Linear Unit (ReLU) functions are used as the activation functions in the DnCNN, we propose a deep-CNN that uses the following soft shrinkage2 $$$F_{Sh}$$$ as an activation function (Fig. 2):
$$F_{Sh}(x,T)= \begin{cases}x-T&(x{\gt}T)\\x+T&(x{\lt}-T)\\0&(-T{\leqq}x{\leqq}T)\end{cases}$$
Where $$$T(T{\gt}0)$$$ is a threshold, and $$$T$$$ is switched proportionally to the noise level $$$\sigma$$$ (e.g., standard deviation of the noise) of the input image:
$$T={\alpha}{\sigma}$$
The coefficient $$$\alpha$$$ of each activation function is optimized as one of the network parameters in the training process. In the denoising process, noise level of the input image may be set to the $$$\sigma$$$.
Results and discussion
We prepared clean volume images, each with a NEX of 10. The averaging process contains in-plane motion compensation to reduce motion blur. Signal intensities of each volume image are normalized to [0, 255]. These clean images were used as ground truth and noisy images were simulated by adding Gaussian noise to clean images.For training, 10 volumes containing 180 slices were used. The dataset contains multi-contrast images of two tissues, for example T2W of brain and knee, T1W of brain, PD of knee and so on. The standard deviation σ of the noise is randomly selected in the range [0, 55] for each input noisy image.
The number of channels of the convolution in the feature extraction layer and the feature conversion layer was set to 64, and the convolution in the residual image generation layer had a single channel. The convolution size was set to 3 × 3 in all the convolutions. The number of feature conversion layers was set to 15. The number of epochs was 200.
For a test, another T2W brain volume data containing 13 slices is used. Shown in Table 1 is the result of a denoising experiment. The noise level is set to σ=5, 10, 20 and 40. BM3D3 is a denoising method thad does not use CNNs and is adjustable to noise level. PSNR of the proposed method is higher than those of BM3D.
Fig. 3(a) is a T2W Fatsat reverse image acquired by 3-T MRI scanner using a 32-ch PI coil. Its boxel size is 0.2×0.2[mm], NEX is 1 and thickness of slice is 3[mm]. Fig. 3(b) is a close-up of Fig. 3(a). Fig. 3(c) is a result of the BM3D and Fig. 3(d) is that of the proposed method. In this experiment, the noise level used for denoising was given manually. A texture marked by the red circle in Fig. 3(d) is finer than that of Fig. 3(c). In Fig. 3(c), banded artifacts are found in the blue circle, but the artifacts are not found in Fig. 3(d).
Conclusion
In order to adjust one network to various noise levels, we proposed a deep convolutional neural network that uses soft shrinkage for activation functions. In experiments using noise-simulated images, PSNR of the proposed method exceeds that of the conventional method adjustable to the noise levels.Acknowledgements
No acknowledgement found.References
1. Zhang K, Zuo W, Chen Y, Meng D, Zhang L, Beyond a Gaussian Denoiser: Residual Learning of Deep CNN for Image Denoising. IEEE Transaction on Image Processing 2017;16 (7), 3142-3155.2. Donoho D. L, De-noising by soft-thresholding. IEEE Transactions on Information Theory 1995;41 (3), 613-627.
3. Dabov K, Foi A, Katkovnik V, Egiazarian K, Image denoising by sparse 3D transform-domain collaborative filtering. IEEE Transactions on Image Processing 2007;16 (8), 2080-2095.
Figures
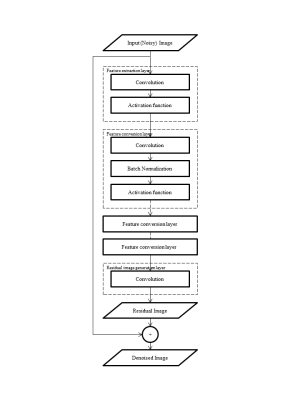
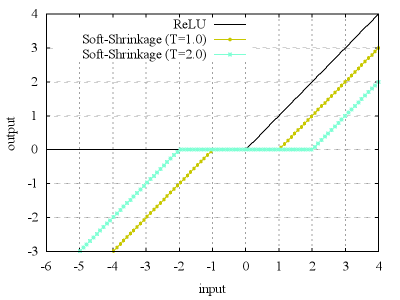
Fig. 2. Activation functions used in this article. The Rectified Linear Unit (ReLU) function is used as the activation functions in the DnCNN. We propose a deep-CNN that uses the following soft shrinkage $$$F_{Sh}$$$ as an activation function:
$$F_{Sh}(x,T)= \begin{cases}x-T&(x{\gt}T)\\x+T&(x{\lt}-T)\\0&(-T{\leqq}x{\leqq}T)\end{cases}$$
Where $$$T(T{\gt}0)$$$ is a threshold, and $$$T$$$ is switched proportionally to the noise level $$$\sigma$$$ (e.g., standard deviation of the noise) of the input image:$$T={\alpha}{\sigma}$$The coefficient $$$\alpha$$$ of each activation function is optimized as one of the network parameters in the training process.
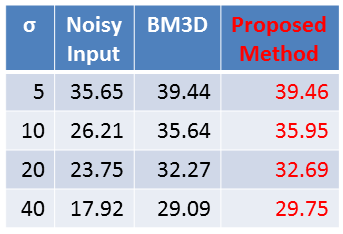
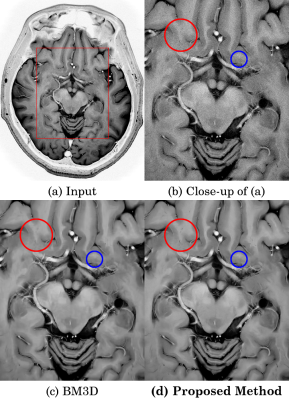
Fig. 3. Result of Denoising.
(a): T2W Fatsat reverse image acquired by 3-T MRI scanner using a 32-ch PI coil (Boxel size: 0.2×0.2[mm], NEX: 1, thickness of slice: 3[mm])
(b): Close-up of (a).
(c): Result of the BM3D.
(d): Result of the proposed method.
A texture marked by the red circle in (d) is finer than that of (c). In (c), banded artifacts are found in the blue circle, but the artifacts are not found in (d).