Introduction

The clinical use of dynamic MRI applications requires the combination of fast data acquisition and low-delay reconstruction. Known suitable methods for the reconstruction of images from highly undersampled k-space data include stack-of-stars trajectory (i.e. a stack of 2D golden-angle radial trajectories) and compressed sensing with temporal constraints.¹ However, many frames (e.g. an entire series of dynamic images) are required to evaluate temporal constraints and thus this approach is not suitable for low-delay reconstruction. For low-delay reconstruction, single-image reconstruction methods are preferred. An example of such methods is the use of a DNN from a single input image to a single output image.² However, this approach requires a higher number of spokes than the method based on temporal constraints since it does not use temporal correlations.

Methods

In order to integrate spatial and temporal correlations and achieve low-delay reconstruction, the author proposes a dynamic reconstruction method using a DNN whose inputs and output are, respectively, consecutive $$$M$$$ frames of neighboring $$$N$$$ slices and a single image to be reconstructed. As shown in Fig. 1, the proposed method reconstructs images in a frame-by-frame manner. Since each frame depends on only $$$(M-1)/2$$$ future frames, the reconstruction delay time is expected to be lower than methods based on compressed sensing. Note that the proposed method can be considered as an extension of a conventional reconstruction method using a DNN, which corresponds to the proposed method with $$$M=N=1$$$. The DNN used in the proposed method consists of convolution layers, rectified linear units (ReLU), and residual connections.³ The overview of the DNN is shown in Fig. 2. As a preprocessing step, a Fast Fourier Transform (FFT) is applied in the stack direction. For each 2D radial k-space frame, an initial image is reconstructed using a non-uniform FFT (NUFFT) and parallel imaging (PI).⁴ The method for reconstructing an initial image does not rely on spatial and temporal correlations with other images. Spatial and temporal correlations are integrated into the DNN. An intermediate layer consists of a convolution layer with $$$3 \times 3$$$ kernel and a ReLU. A residual connection is inserted for each 2 stacked intermediate layers. The number of intermediate layers is 10. The first and the last layer consist of only convolution layers with $$$1 \times 1$$$ kernel. The number of channels in each intermediate layer is 128. Datasets from 2 volunteers were acquired for training. A dataset from 1 volunteer was acquired for validation. All datasets include 5 Cartesian images with matrix size $$$256 \times 160 \times 16$$$. In addition, the validation dataset includes actual k-space data using a stack-of-stars trajectory. For each radial k-space frame, 21 spokes were assigned. The number of input images were set to $$$M=5$$$ and $$$N=3$$$ for the proposed method. For generating the inputs of the DNN, 10 frames were generated from the Cartesian images by simulating a radial sampling. The DNN was trained by Adaptive moment estimation (Adam) with a mean-squared-error loss function.

Results

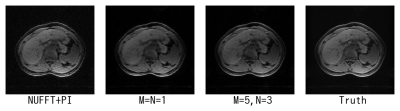
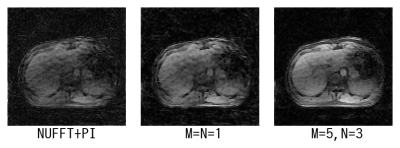
The results using simulated radial data are shown in Fig. 3. The results for actual stack-of-stars data are shown in Fig. 4. The quality of the images reconstructed using the proposed scheme ($$$M=5, N=3$$$) is clearly improved over the images reconstructed using an NUFFT+PI and the existing scheme ($$$M=N=1$$$). In particular, the results for actual stack-of-stars data demonstrate that structures within the liver are more clearly depicted by using spatial and temporal correlations.

Discussion

The results showed that the proposed method could reconstruct dynamic images from $$$21$$$ spokes per frame, which was significantly lower than $$$45$$$ spokes reported in a projection reconstruction method using DNN.² The results showed that the quality of images from actual stack-of-stars data was lower than that from simulated radial data. To improve the image quality, the author suggests that imperfections of MRI system sampling should be accounted for in the simulation of radial sampling. Improvement of the simulation is deferred to future work.

Conclusion

This paper proposes a novel reconstruction method integrating spatial and temporal correlations into a DNN. Unlike methods based on compressed sensing, the proposed method reconstructs images in a frame-by-frame manner and thus can be used for low-delay reconstruction. Experimental results show that the proposed method is effective for reconstruction of highly undersampled radial dynamic images.

Acknowledgements

The author thanks Mr. Yui for providing MR images.