2793

Data-Driven Image Contrast Synthesis from Efficient Mixed-Contrast Sequences
Jonathan I Tamir1, Valentina Taviani2, Shreyas S Vasanawala3, and Michael Lustig1

1Electrical Engineering and Computer Sciences, University of California, Berkeley, Berkeley, CA, United States, 2MR Applications and Workflow, GE Healthcare, Menlo Park, CA, United States, 3Radiology, Stanford University, Stanford, CA, United States

Synopsis

Synthetic MR is an attractive paradigm for generating diagnostic MR images with retrospectively chosen scan parameters. Typically, synthetic MR images are produced by collecting measurements at multiple measurement times and fitting to a physical model. Here we propose a two-step approach to contrast synthesis. First, we solve a regularized linear inverse problem to reconstruct images at multiple measurement times. Second, we classify spatio-temporal signals and apply different linear combinations based on the classification. We demonstrate the approach on retrospectively under-sampled T1 Shuffling data, in which 3D FSE is collected at relatively short repetition times (TR), and combined to synthesize image contrast with a long TR. The data-driven approach may be useful for synthesizing MR contrasts from acquisitors with varying measurement parameters.

Introduction

Synthetic MR is an attractive paradigm for generating diagnostic MR images with retrospectively chosen scan parameters [1]. Typically, synthetic MR images are produced in two stages. First, data collected at multiple measurement times are reconstructed or fit to a physical-based model. The model may be explicit, e.g. with Bloch equations [1-4]; or it may be implicit, e.g. using subspace constraints [5-10]. Next, the result is used to synthesize image contrasts, e.g. through forward propagation of the Bloch equations or through linear combinations of the subspace images. The explicit approach has the advantage of leveraging prior physical information and enabling the use of non-linear equation fits, but it may introduce error when the model does not adequately explain the data, e.g. due to partial voluming, flow, or system imperfections. The implicit approach benefits from a relaxed model constraint, but is limited in expressibility due to the linearity.

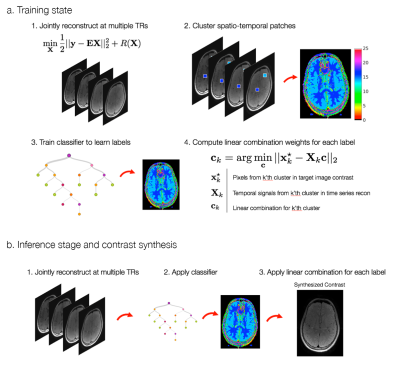
Here we propose a two-step approach to contrast synthesis, inspired by ideas from the RAISR technique for image super-resolution [11]. First, we solve a regularized linear inverse problem to jointly reconstruct images at multiple measurement times. Second, we classify spatio-temporal patches into distinct classes and apply linear combinations tailored to each class. The two-step approach combines the robustness of regularized linear reconstructions with the expressibility of non-linear classification.

As proof of principle, we apply the approach to increase the scan efficiency of proton-density volumetric fast spin-echo (3DFSE) imaging in the brain. Conventional 3DFSE sequences use long repetition times (TR) to acquire T2-weighted and proton density contrast. To increase scan efficiency, long echo train lengths (ETL) are used, leading to blurring due to T2 decay [12]. We increase scan efficiency by acquiring at multiple, shorter TRs, a technique we call T1 Shuffling [8]. This enables a reduction in the ETL at the expense of T1-weighted contamination. We de-emphasize the T1 weighting and recover a proton-density image by applying the proposed data-driven contrast synthesis. The approach is summarized in Fig 1.

Theory

A time series of training images $$$\mathbf{X}=\begin{bmatrix}\mathbf{x}_1&\mathbf{x}_2&\cdots&\mathbf{x}_T\end{bmatrix}^\top$$$ is reconstructed from multi-channel k-space data, $$$Y$$$, through a linear inverse problem:$$\min_{\mathbf{X}}||\mathbf{Y}-\mathbf{E}\mathbf{X}||_2^2+R(\mathbf{X}),$$where $$$\mathbf{E}$$$ is the SENSE-based [13] forward operator consisting of estimated coil sensitivities and optionally a subspace constraint, and $$$R$$$ is a regularization term. Given a reconstruction $$$\mathbf{X}$$$ and a target image contrast $$$\mathbf{x}^\star$$$, spatio-temporal patches are extracted from the concatenation,$$\mathbf{\bar{X}}=\begin{bmatrix}\mathbf{X}\\\mathbf{x}^\star\end{bmatrix},$$normalized, and clustered with K-means, providing labels for each pixel in $$$\mathbf{x}^\star$$$. For each cluster, a linear combination is fit between the time series and the target value:$$\mathbf{c}_k=\arg\min_{\mathbf{c}}||\mathbf{x}^\star_k-\mathbf{X}_k\mathbf{c}||\quad{}k=1,\dots,K,$$where $$$\mathbf{x}^\star_k$$$ and $$$\mathbf{X}_k$$$ are the pixels in $$$\mathbf{x}^\star$$$ and in $$$\mathbf{X}$$$ with label $$$k$$$, respectively. After obtaining the clusters, a classifier is trained to map the spatio-temporal patches back to the corresponding labels. At testing time, a new reconstructed image time series is classified into labels using the classifier, and the precomputed linear combinations are applied to obtain an image contrast.

Methods

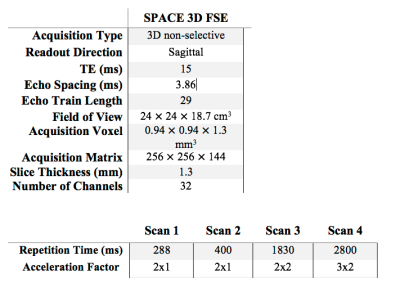
Two volunteers were scanned with IRB approval at 3T on a Siemens Trio, with a brain protocol consisting of separate 3DFSE acquisitions (scan parameters in Table 1). The data were coil-compressed [14] to 12 channels and coil sensitivities were estimated using ESPIRiT [15]. The image corresponding to TR=2800, i.e. proton density, was chosen as the target image contrast, and the images corresponding to TRs=(288 ms, 400 ms, 1830 ms) were chosen as the time series. Using the first volunteer data, patches of size 3x3 were used for K-means with $$$K=15$$$ clusters to create labeled images across 40 slices. A decision tree classifier was trained to map the spatio-temporal patches to the labels with 10-fold cross-validation. The images from the second volunteer were used for testing, whereby patches were classified into a label and the learned linear combination was applied. Image reconstructions were performed with BART [16] and clustering/classification was performed in MATLAB.

Results and Discussion

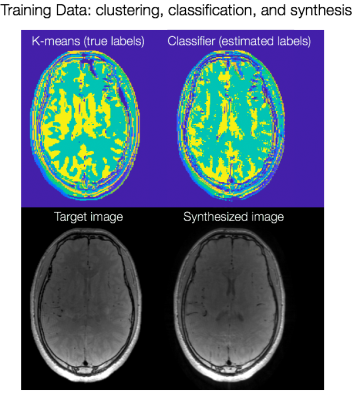
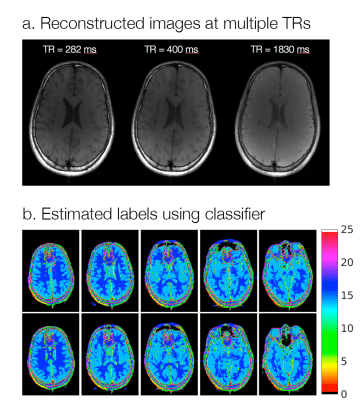
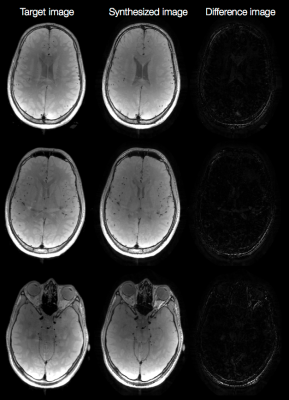
Fig. 2a shows the result of K-means clustering and the corresponding classified labels on one slice from the training data. The discrepancies in the two maps show that incorrect linear combinations may be used for some pixels, and can lead to errors in the synthesized image (Fig. 2b). Fig. 3a shows axial reconstructions of the three short TR scans from the second volunteer used for testing. Fig. 3b shows the label map after classification across 10 slices. Fig. 4 shows the target image contrast and the data-driven contrast synthesis for three of the 10 representative slices. The overall contrast is captured, though errors in classification lead to errors in contrast synthesis. We expect these errors to reduce as training data is increased to include multiple subjects.

Conlcusion

Data-driven contrast synthesis may be useful for synthesizing MR contrasts from acquisitions with varying measurement parameters.

Acknowledgements

We thank Karthik Gopalan and Zhiyong Zhang for their generous time and support with the data collection. We also thank the following funding sources: NIH Grants R01EB019241, R01EB009690, and P41RR09784, Sloan Research Fellowship, Okawa Research Grant, and GE Healthcare.

References

  1. J. B. M. Warntjes, O. D. Leinhard, J. West, and P. Lundberg, “Rapid Magnetic Resonance Quantification on the Brain: Optimization for Clinical Usage,” Magnetic Resonance in Medicine, vol. 60, no. 2, pp. 320–329, 2008.
  2. D. Ma, V. Gulani, N. Seiberlich, K. Liu, J. L. Sunshine, J. L. Duerk, and M. A. Griswold, “Magnetic Resonance Fingerprinting,” Nature, vol. 495, no. 7440, pp. 187–192, 2013.
  3. Pedro Gómez, Guido Buonincontri, Miguel Molina-Romero, Jonathan Sperl, Marion Menzel, Bjoern Menze. “Accelerated Parameter Mapping with Compressed Sensing: an Alternative to MR Fingerprinting.” ISMRM 25th Annual Meeting, 1167. Hawaii, 2017.
  4. Zhao, Bo, Fan Lam, Berkin Bilgic, Huihui Ye, and Kawin Setsompop. "Maximum Likelihood Reconstruction for Magnetic Resonance Fingerprinting." IEEE Xplore (2015): doi:10.1109/ISBI.2015.7164017
  5. Nataraj, Gopal, Jon-Fredrik Nielsen, Clayton Scott, and Jeffrey A Fessler. "Dictionary-Free MRI PERK: Parameter Estimation Via Regression with Kernels." Eprint ArXiv:1710.02441. October, 2017
  6. Huang, Chuan, Christian G Graff, Eric W Clarkson, Ali Bilgin, and Maria I Altbach. "T2 Mapping From Highly Undersampled Data by Reconstruction of Principal Component Coefficient Maps Using Compressed Sensing." Magnetic resonance in medicine 67, no. 5 (2012): doi:10.1002/mrm.23128
  7. Tamir, Jonathan I, Martin Uecker, Weitian Chen, Peng Lai, Marcus T Alley, Shreyas S Vasanawala, and Michael Lustig. "T2 Shuffling: Sharp, Multicontrast, Volumetric Fast Spin-echo Imaging." Magnetic resonance in medicine (2016)doi:10.1002/mrm.26102.
  8. Jonathan Tamir, Valentina Taviani, Shreyas Vasanawala, Michael Lustig. “T1-T2 Shuffling: Multi-Contrast 3D Fast Spin-Echo with T1 and T2 Sensitivity” ISMRM 25th Annual Meeting, 451. Hawaii, 2017
  9. Zhao, Bo, Kawin Setsompop, Elfar Adalsteinsson, Borjan Gagoski, Huihui Ye, Dan Ma, Yun Jiang, P Ellen Grant, Mark A Griswold, and Lawrence L Wald. "Improved Magnetic Resonance Fingerprinting Reconstruction with Low-rank and Subspace Modeling." Magnetic resonance in medicine (2017)doi:10.1002/mrm.26701.
  10. Assländer, Jakob, Martijn A Cloos, Florian Knoll, Daniel K Sodickson, Jürgen Hennig, and Riccardo Lattanzi. "Low Rank Alternating Direction Method of Multipliers Reconstruction for MR Fingerprinting." Magnetic resonance in medicine (2017)doi:10.1002/mrm.26639
  11. Romano, Yaniv, John Isidoro, and Peyman Milanfar. "RAISR: Rapid and Accurate Image Super Resolution." IEEE Transactions on Computational Imaging 3, no. 1 (2017): doi:10.1109/tci.2016.2629284
  12. Busse, Reed F, Hari Hariharan, Anthony Vu, and Jean H Brittain. "Fast Spin Echo Sequences with Very Long Echo Trains: Design of Variable Refocusing Flip Angle Schedules and Generation of Clinical T2 Contrast." Magnetic resonance in medicine 55, no. 5 (2006): doi:10.1002/mrm.20863
  13. Pruessmann, K P, M Weiger, M B Scheidegger, and P Boesiger. "SENSE: Sensitivity Encoding for Fast MRI." Magnetic resonance in medicine 42, no. 5 (1999): 952-62
  14. Zhang, Tao, John M Pauly, Shreyas S Vasanawala, and Michael Lustig. "Coil Compression for Accelerated Imaging with Cartesian Sampling." Magnetic resonance in medicine 69, no. 2 (2013): doi:10.1002/mrm.24267.
  15. Uecker, Martin, Peng Lai, Mark J Murphy, Patrick Virtue, Michael Elad, John M Pauly, Shreyas S Vasanawala, and Michael Lustig. "ESPIRiT-an Eigenvalue Approach to Autocalibrating Parallel MRI: Where SENSE Meets GRAPPA." Magnetic resonance in medicine 71, no. 3 (2014): doi:10.1002/mrm.24751
  16. M Uecker, F Ong, JI Tamir, D Bahri, P Virtue, JY Cheng, T Zhang, M Lustig. Berkeley Advanced Reconstruction Toolbox, Annual Meeting ISMRM, Toronto 2015, In Proc. Intl. Soc. Mag. Reson. Med 23; 2486 (2015)

Figures

Figure 1. Overview of the method, inspired by the RAISR technique for image super-resolution. a. In the training stage, spatio-temporal patches from a reconstructed time series of images are clustered using K-means. From the clusters, a classifier is trained to label new patches and a linear combination is learned to map each cluster to a target image contrast. b. At inference time, a new reconstructed time series of images is classified into labels, and the appropriate linear combination is applied to each pixel according to its label.

Figure 2. Acquisition parameters used across all 3D FSE scans, and the corresponding repetition times and parallel imaging acceleration factors for each scan.

Figure 3. A slice from the training data with high classification error. The labels from K-means clustering (left) differ from those obtained using the classifier (right). Errors in classification can lead to incorrect contrast in the synthesized image.

Figure 4. a. Reconstructed images at multiple TRs for a slice from the second volunteer, used for testing. b. Estimated labels on 10 slices the using the learned classifier.

Figure 5. Target proton density (left), synthesized proton density (middle), and difference images (right) of three representative slices from the test data. The synthesized image contrasts show good agreement with the target image, but have have slightly reduced gray matter-white matter contrast.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
2793