Synopsis

End-to-end learning of the image reconstruction domain transform with AUTOMAP (Automated Transform by Manifold Approximation) has been demonstrated on a variety of spatial encoding strategies previously limited to single-channel data. We extend this framework to learning reconstruction of highly undersampled multichannel k-space data solely from pairs of multichannel k-space and image training data without employing conventional parallel imaging formulations such as SENSE or GRAPPA, and show improved RMSE and artifact reduction with the trained AUTOMAP reconstruction network.

PURPOSE

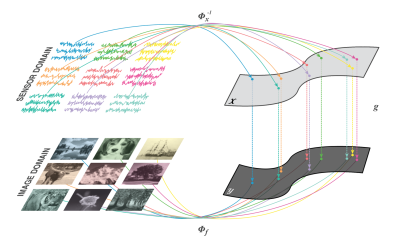
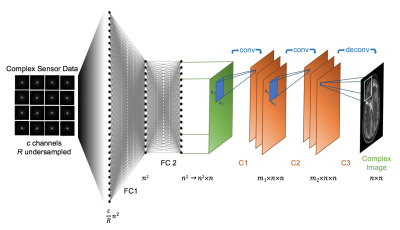
Automated Transform by Manifold Approximation (AUTOMAP)^1,2 is a generalized MR image reconstruction framework based on supervised manifold learning and universal function approximation (Figure 1) implemented with a deep neural network architecture (Figure 2). Previous work demonstrated the ability of AUTOMAP to learn the reconstruction of spatially encoded raw data solely from pairs of k-space and image training data, without utilizing explicit operations such as the Fourier Transform or post-processing modules such as gridding or density compensation.

Here we demonstrate extension of the AUTOMAP framework to learning reconstruction of highly undersampled multichannel k-space data. This supervised learning is implemented with a non-iterative feedforward neural network, without use of conventional parallel imaging formulations such as SENSE³ or GRAPPA⁴.

METHODS AND EXPERIMENTS

The typical approach reconstruction of multichannel MR data employs the Fourier Transform to perform spatial decoding, which requires solving and/or applying a linear regression model either in k-space (e.g., missing sample estimation for GRAPPA) or image space (e.g., unaliasing in SENSE) to remove aliasing artifacts for undersampled acquisitions. Our data-driven approach to solve for the reconstruction function involves simultaneously learning the undersampled spatial decoding and coil combination operations, jointly represented by a highly-parameterized nonlinear neural network:

$$ I(x,y)=σ(W_{fc2} (σ(W_{fc1} S(k_{x,y} )+b_{fc1} )+b_{fc2} )*W_{c1}*W_{c2} *^T W_{c3} $$

where the k-space samples from individual coils $$$S(k_x,k_y)$$$ are concatenated to form the complex vector input $$$S(k_{x,y})$$$, and $$$W_{fc1}$$$ and $$$W_{fc2}$$$ are complex-valued weight matrices, $$$b_{fc1}$$$ and $$$b_{fc2}$$$ are a complex-valued offset vector of dimensionality $$$d$$$, and $$$σ$$$ is the hyperbolic tangent activation function. These fully-connected layers approximate the between-manifold projection from the individual coil k-space data to the final image via the universal approximation theorem⁵. This joint spatial encoding and coil-combination function approximation is further constrained by convolutional layers with kernel weights $$$W_{c1}$$$,$$$W_{c2}$$$, and $$$W_{c3}$$$ that force the image to be sparsely represented in the convolutional feature space. The resultant reconstruction function is optimized for a domain of relevant data (e.g. brain images) during training and is thus less sensitive to unrepresentative input corruptions such as noise.

The supervised learning process employed a training corpus of 50,000 pairs of $$$S(k_{x,y})$$$ and $$$I(x,y)$$$. For this work, the images $$$I(x,y)$$$ were collected from Human Connectome Project⁶ T1-weighted anatomical brain images, and forward-encoded to form $$$S_c(k_x,k_y)=FT(I(x,y)C_c(x,y))$$$, where the complex coil sensitivity profiles of a 32-channel head coil $$$C_c$$$ was obtained from an actual scan. Because of GPU memory limitations, the channel data were mixed down to 16 modes using standard global SVD-based compression before the undersampling process described in more detail below. The weights of the neural network model were updated via stochastic gradient descent and backpropagation to minimize the mean-square error loss between network output and target images.

Multichannel T2-weighted data were acquired on a 3T Siemens Trio with the standard Siemens 32-channel head array coil, whose coil sensitivity profiles are used in the training described above. A turbo spin echo sequence with 224×224 mm² field of view was acquired across 35 slices with a 30% distance factor. The imaging parameters are as follows: TR=6.1 s, TE=98 ms, flip angle=150°, and a resolution of 0.5 × 0.5 × 3.0 mm³ with a matrix size of 448 × 448. The fully sampled uncombined complex k-space data were retrospectively undersampled to a 112 × 112 matrix, corresponding to 2 mm in-plane resolution. Iterative SENSE reconstruction³ was performed using the GMRES solver⁷ with stopping criteria of 1e-4 relative error to generate the ground truth reconstruction, which was modulated by the sensitivity profiles and then mixed down to 16 modes using the standard global SVD-based compression. This multichannel data were then undersampled by 15.5x with an R=4 x 4 coherent undersampling pattern and 5 x 5 low frequency region, and reconstructed with AUTOMAP and SENSE using the SVD coil sensitivity profiles. The AUTOMAP network was trained on HCP brain images modulated by the SVD coil sensitivity profiles to produce the multichannel training data. Each channel was Fourier transformed and correspondingly undersampled with the same R=15.5x pattern, and channels were concatenated at the network input.

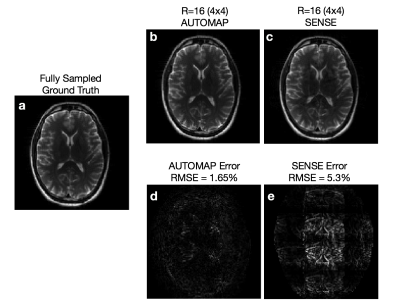
With reference to ground truth (Figure 3a), we observe for the R=4 x 4 undersampled reconstructions higher accuracy with AUTOMAP (Figure 3b) in comparison with SENSE (Fig 3c), with reduced noise and reconstruction artifacts. This can be more clearly observed in the error maps (Figure 3d-e) and quantified by a 3-fold reduction in RMSE (1.65% vs 5.3%). This improvement in reconstruction performance is likely due to AUTOMAP extracting important data interdependency relationships learned during training1, which becomes more valuable as the available spectral content supplied for the reconstruction is reduced with higher undersampling factors. Parameterization over a range of undersampling factors and patterns is planned for future investigation.

Acknowledgements

References

[1] Zhu, B., Liu, J. Z., Rosen, B. R., & Rosen, M. S. Image reconstruction by domain transform manifold learning. arXiv preprint arXiv:1704.08841 (2017).

[2] Zhu, B., Liu, J. Z., Rosen, B. R., & Rosen, M. S. Neural Network MR Image Reconstruction with AUTOMAP: Automated Transform by Manifold Approximation, Proc. Intl. Soc. Mag. Reson. Med., 25 p.0640 (2017)

[3] Pruessmann, Klaas P., et al. "SENSE: sensitivity encoding for fast MRI." Magnetic resonance in medicine 42.5 (1999): 952-962.

[4] Griswold, Mark A., et al. "Generalized autocalibrating partially parallel acquisitions (GRAPPA)." Magnetic resonance in medicine 47.6 (2002): 1202-1210.

[5] Cybenko, G. Approximation by superpositions of a sigmoidal function. Math. Control Signal Systems 2, 303–314 (1989)

[6] Fan, Q. et al. MGH–USC Human Connectome Project datasets with ultra-high b-value diffusion MRI. NeuroImage 124, 1108–1114 (2016)

[7] Saad, Y. & Schultz, M. H. GMRES: A Generalized Minimal Residual Algorithm for Solving Nonsymmetric Linear Systems. SIAM Journal on Scientific and Statistical Computing 7, 856–869 (2006).