Synopsis

Fluid-attenuated inversion recovery (FLAIR) MRI pulse sequence is used clinically and in research for the detection of WM lesions. However, in a clinical setting, some MRI pulse sequences can be missing because of patient or time constraints. We propose 3D fully convolutional neural networks to predict a FLAIR MRI pulse sequence from other MRI pulse sequences. We evaluate our approach on a real multiple sclerosis disease dataset by assessing the lesion contrast and by comparing our approach to other methods. Both the qualitative and quantitative results show that our method is competitive for FLAIR prediction.

Introduction

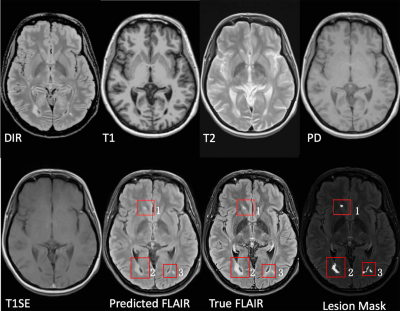
Multiple sclerosis (MS) is a demyelinating and inflammatory disease of the central nervous system.¹ MS has been characterized as a white matter (WM) disease with the formation of WM lesions, which can be visualized by magnetic resonance imaging (MRI).^2,3 FLAIR is commonly used clinically and in research to detect WM lesions which appear hyperintense compared to normal WM tissue. Additionally, observer performance is better with FLAIR,⁴ as shown in Fig. 1. However, in a clinical setting, some MRI pulse sequences can be missing because of patient or time constraints. Hence, there is a big need for predicting the missed FLAIR when it was not acquired during a patient's visit. Furthermore, it was shown in some publications^5,6 that synthesized MR images can improve brain tissue classification and segmentation results, which is an additional motivation for this work. FLAIR may also be absent in some legacy research datasets, that are still of major interest due to their number of subjects and long follow-up.

We propose 3D Fully Convolutional Neural Networks (3D FCNs) to predict FLAIR. The proposed method can learn an end-to-end and voxel-to-voxel mapping between other MRI pulse sequences and the corresponding FLAIR. Finally, the feasibility of our approach is validated qualitatively and quantitatively.

Method

Our goal is to predict FLAIR by finding a non-linear function $$$s$$$, which maps multi-sequence source images $$$I_{\mathrm{source}}$$$, e.g. $$$I_{\mathrm{source}}=\left(I_{\mathrm{T1}},I_{\mathrm{T2}}\right)$$$, to the corresponding target image $$$I_{\mathrm{target}}$$$. The non-linear function can be found by solving the following optimization problem:$$\hat{s\ }=\arg\min_{s \in S} \sum_{i=1}^{n}Error(I^{i}_{\mathrm{target}},s(I^{i}_{\mathrm{source}}))$$where $$$S$$$ denotes potential mapping functions, $$$n$$$ is the number of subjects. The error function above calculates the difference between the predicted and the true image.

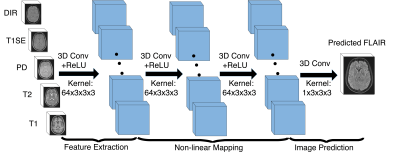
Our 3D FCNs is shown in Fig. 2. It contains three convolutional layers followed by rectified linear functions ($$$relu(x)=max(x,0)$$$). Every layer $$$l \in [1,L]$$$ has $$$C_{l}$$$ feature maps. The first layer extracts $$$C_{l}$$$-dimensional features from input images. Then, the second and third layers find a non-linear mapping between the feature representations of source images and the target image feature representations, which are used to reconstruct our target image. The $$$m_{\mathrm{th}}$$$ feature map in the $$$l_{\mathrm{th}}$$$ layer is defined as follows:$$y_{l}^{m}=max(0,\sum_{c=1}^{C_{l-1}}k_{l}^{m,c}*y_{l-1}^{c}+b_{l}^{m})$$where $$$k$$$ denotes a 3-dimensional trainable kernel and $$$b$$$ is a learned bias. The parameters $$$k,b$$$ can be learned by minimizing the error function, which is mean-square-error (MSE) in our model. $$MSE = \frac{1}{H \times W \times D}\sum_{h=1}^{H}\sum_{w=1}^{W}\sum_{d=1}^{D}(y_{h,w,d}-\hat{y\ }_{h,w,d})^{2}$$where $$$H,W,D$$$ indicate the height, weight, and depth of the target image, while $$$y$$$ and $$$\hat{y\ }$$$ are the ground truth and the predicted image, respectively.

To evaluate our method, we compare it qualitatively and quantitatively with three other approaches : modality propagation⁷, random forests (RF) with 60 trees⁸, and voxel-wise multilayer perceptron (MLP). Specifically, two metrics are used to evaluate quantitatively: 1). Mean-Square-Error (MSE); 2). Peak Signal-to-noise-Ratio (PSNR).

Experiments and Results

We used our in-house dataset for FLAIR prediction, which contains 4 healthy volunteers and 20 MS patients, including T1-w, T2-w, T1 spin-echo (T1SE), proton density (PD), and double inversion recovery (DIR) weighted images and the corresponding FLAIR. Five-fold cross validation is used for evaluating performance. In 5-fold cross validation, the dataset is partitioned into 5 folds. Subsequently 5 iterations of training and validation are performed such that within each iteration one different fold is held-out for validation and remaining four folds are used for training.

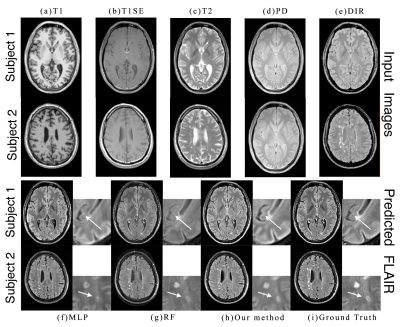
Fig. 3 shows the inputs and outputs. As shown with arrows, some regions can be better predicted by our method. The modality propagation method got the worst result, so we do not show it here.

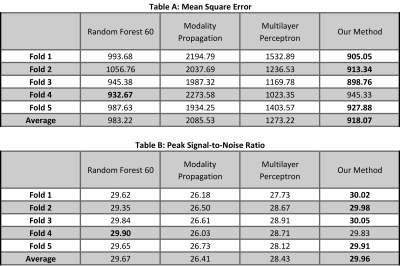
Fig. 4 shows the result on 5-fold cross validation. Our method gets the best result on four folds. Even though RF gets the best performance on fold-4, the error difference is very small.

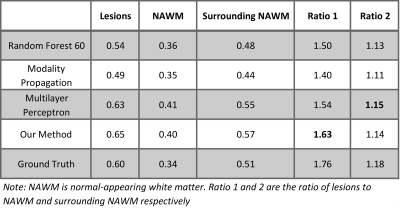
Figure 5 is the evaluation result for MS lesion contrast. MS lesions, normal-appearing WM (NAWM), and the surrounding NAWM are extracted using lesion and WM masks. Then we calculated the mean intensity of these three regions in the predicted images and ground truth. Our method keeps a good contrast between MS lesions and white matter, which is clinically very useful.

Conclusion

We introduced 3D FCNs for FLAIR prediction from multi-sequence MR images. The nonlinear relationship between the source images and FLAIR can be captured by our network. Both the qualitative and quantitative results show its good performance for FLAIR prediction. Moreover, the generated FLAIR has a good contrast for MS lesions so that it can be useful clinically. In the future, it would be interesting to also assess the utility of the method in the context of other WM lesions (e.g. age-related hyperintensities).

Acknowledgements

References

1. A. Compston and A. Coles. Multiple sclerosis. Lancet, 372(9648):1502–1517, 2008.
2. D. W. Paty, J. J. Oger, L. F. Kastrukoff, S. A. Hashimoto, J. P. Hooge, A. A. Eisen, K. A. Eisen, S. J. Purves, M. D. Low, and V. Brandejs. MRI in the diagnosis of MS: a prospective study with comparison of clinical evaluation, evoked potentials, oligoclonal banding, and CT. Neurology, 38(2):180–185, 1988.
3. F. Barkhof, M. Filippi, D. H. Miller, P. Scheltens, A. Campi, C. H. Polman, G. Comi, H. J. Ader, N. Losseff, and J. Valk. Comparison of MRI criteria at first presentation to predict conversion to clinically definite multiple sclerosis. Brain, 120 ( Pt 11):2059–2069, 1997.
4. John H. Woo, Lana P. Henry, Jaroslaw Krejza, and Elias R. Melhem. Detection of simulated multiple sclerosis lesions on t2-weighted and flair images of the brain: Observer performance. Radiology, 241(1):206–212, 2006.
5. Iglesias J.E., Konukoglu E., Zikic D., Glocker B., Van Leemput K., Fischl B. Is Synthesizing MRI Contrast Useful for Inter-modality Analysis?. Medical Image Computing and Computer-Assisted Intervention – MICCAI 2013. Lecture Notes in Computer Science, vol 8149. Springer.
6. van Tulder G., de Bruijne M. Why Does Synthesized Data Improve Multi-sequence Classification? Medical Image Computing and Computer-Assisted Intervention -- MICCAI 2015. Lecture Notes in Computer Science, vol 9349. Springer.
7. Ye D.H., Zikic D., Glocker B., Criminisi A., Konukoglu E. Modality Propagation: Coherent Synthesis of Subject-Specific Scans with Data-Driven Regularization. Medical Image Computing and Computer-Assisted Intervention – MICCAI 2013. Lecture Notes in Computer Science, vol 8149. Springer
8. A. Jog, A. Carass, D. L. Pham, and J. L. Prince. Random Forest FLAIR Reconstruction from T1, T2, and PD -Weighted MRI. Proc IEEE Int Symp Biomed Imaging (ISBI) , 2014:1079–1082, 2014.