2782

A Neural Network for Referenceless Reconstruction in Simultaneous Multi-Slice Imaging

Klaus Eickel^1,2 and Matthias Günther^1,2,3

¹Fraunhofer MEVIS, Bremen, Germany, ²mediri GmbH, Heidelberg, Germany, ³University Bremen, Bremen, Germany

Synopsis

The unwrapping of simultaneous multi-slice images without extra reference data is presented. A trained deep neural network disentangles overlapping image content and creates the final magnitude images. The results are compared to established techniques (split slice-GRAPPA), especially where correct reference data are missing.

Introduction

Simultaneous multi-slice (SMS) imaging ^1–3 has emerged as a promising acceleration technique for magnetic resonance imaging (MRI) since multi-coil systems ⁴ and reconstruction methods like (split) slice-GRAPPA ^5,6 paved the way for a variety of applications. Established reconstruction strategies for SMS utilize spatial encoding information inherent in multi-coil receiver arrays and require additional reference data, i.e. auto-calibration signal (ACS), to disentangle overlapping image content ⁷. In general, ACS-acquisition can be time-consuming and a source of reconstruction-errors.
Here, a deep neural network (DNN) was designed to unfold SMS images without the need of any reference-scans. First, the DNN architecture is introduced. Thereafter, the predicted images are evaluated and deep learning (DL) reconstructions (DLR) are compared to split slice-GRAPPA (SSG) ⁶ where correct ACS is missing.

Methods

Training a DNN requires suitable data. 37 datasets of phantom objects (N=30, fruits and geometric phantoms) and heads (N=7) were used for training (N_train=29) and validation (N_val=8), while evaluation was done on separate datasets of volunteers’ heads (N_test=4). All data were acquired with identical sequence parameters in 3 contrasts (TE=4.9/9.7/14.5ms, TR=126ms, α=70°, matrix: 128x128x6). Rawdata of 20 receiver-coils were preprocessed offline, i.e. 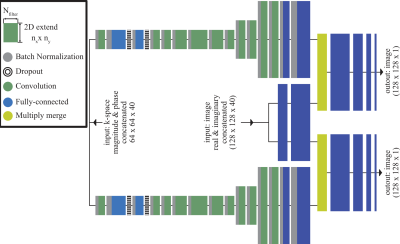simulated SMS acquisition and CAIPIRINHA-shifts ⁸, and augmented by undersampling (90%, 80%, 75%, 70%, 60%, 50%, 40%, 30%) yielding to N_train=2349, N_val=648 datasets for a multiband factor (MB) of MB=2 and N_train=870, N_val=240 for MB=3, respectively. Figure 1 shows the DNN’s architecture where folded (MB=2 or MB=3), uncombined, low-resolution k-space (64x64) and image data (128x128) were fed into the network while sum-of-square combined single-band (SB) images serve as target. SB-images were shifted to the according CAIPIRINHA-pattern. Complex-valued input (Re, Imag) were concatenated along channel dimension (N_ch=40). A user defined loss-function: E = MSE x TV was applied to drive the optimizer. Mean-squared error (MSE) and total-variation error (TV) were combined to account for global errors as well as mismatches on object borders. The DNN was set up in the Keras library ⁹ and training (280 epochs in 28 hours) was performed on a Nvidia GTX1080 graphics card.
All images I of one dataset were normalized to

$$I_n = \frac{I-I_{min}}{I_{max}- I_{min} } \text{ .}$$

Two metrics were introduced for quantification of the differences between reconstructions. The commonly used normalized root mean-squared error (NRMSE) together with subtraction-maps of SB and recovered SMS-images and the structural similarity index (SSIM) ¹⁰. SSIM assesses perceptual image quality by taking advantage of characteristics of the human visual system ¹⁰. It is defined as

$$SSIM(x,y) = L(x,y) \cdot C(x,y) \cdot S(x,y) \text{ ,}$$Abstract

where L , C , S are luminance, contrast and structure for each pixel (x,y) ¹⁰. For NRMSE and mean SSIM (MSSIM) a threshold-mask of 1% was applied to remove noise outside the object.

Results

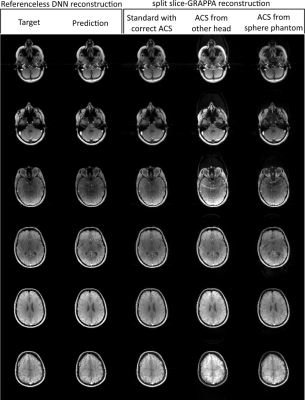
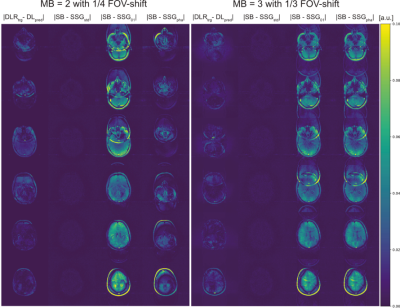
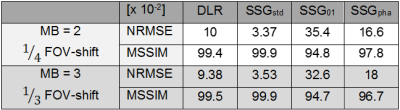
The different reconstruction results are shown in Figure 2. Unseen test data were fed into the trained DNN and its predictions were evaluated and compared to SSG reconstructions with suitable ACS (SSG_std), ACS taken from another object with similar anatomy, i.e. another head, (SSG₀₁) and ACS of a spherical phantom (SSG_pha). All measurements had an identical field-of-view (FOV).
Normalized subtraction-maps (Fig.3) compare DNN's prediction to standard SSG and SSG where correct ACS are missing and replaced by other ACS (SSG₀₁, SSG_pha). SMS-reconstructions for MB=2 with 1/4 FOV-shift (left) and MB=3 (1/3 FOV-shift) (right) are illustrated. Both settings are quantified by NRMSE as tabulated in Table 1.
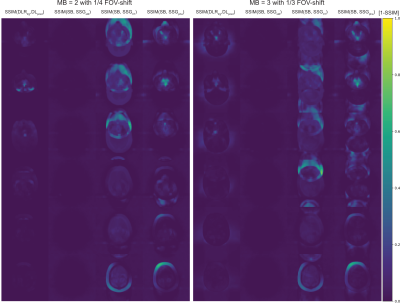
Figure 4 depicts the inverse SSIM-maps (1-SSIM) for the above cases. The corresponding MSSIM are given in Table 1.

Discussion

Visual inspection generally approves the unwrapping of SMS data by a DNN (Fig.2). Although more inter-slice signal leaks into the reconstructed slices, DLR outperforms SSG where ACS data are missing or corrupted. SSIM allows more perceptual than purely pixel-wise evaluation of the different approaches and emphasizes the above impression. Nevertheless, reconstruction errors especially inside the region of interest cannot clearly be distinguished from pathological findings at this stage. The limited amount of trainings data and the broad spectrum of these (fruits, phantoms, heads) may have prevented more efficient training. As in other DL scenarios, it is likely that the performance can be significantly increase when additional training data are included, ideally these would be provided by a large database with in-vivo raw-data.

Conclusion

A novel approach to reconstruct SMS images without additional ACS is presented. Although, clearly more reconstruction artifacts as for a correct SSG reconstruction occur, DLR is beneficial to SSG with incorrect reference data. This might be especially useful for dynamic imaging in presents of motion or for emergency-protocols as no ACS is needed and demanded computational load is low.

Acknowledgements

The authors gratefully thank Markus Wenzel and Hans Meine for valuable, interdisciplinary discussions on deep learning in image-processing.

References

1. Weaver JB. Simultaneous multislice acquisition of MR images. Magn Reson Med 1988;8:275–284. 2. Müller S. Multifrequency selective rf pulses for multislice MR imaging. Magn Reson Med 1988;6:364–371. 3. Souza SP. Simultaneous Multislice Acquisition of MR Images by Hadamard-Encodes Excitation SOUZA_1988.pdf. 4. Larkman DJ, Hajnal J V., Herlihy AH, Coutts GA, Young IR, Ehnholm G. Use of multicoil arrays for separation of signal from multiple slices simultaneously excited. J Magn Reson Imaging 2001;13:313–317. 5. Setsompop K, Gagoski BA, Polimeni JR, Witzel T, Wedeen VJ, Wald LL. Blipped-controlled aliasing in parallel imaging for simultaneous multislice echo planar imaging with reduced g-factor penalty. Magn Reson Med 2012;67:1210–1224. 6. Cauley SF, Polimeni JR, Bhat H, Wald LL, Setsompop K. Interslice leakage artifact reduction technique for simultaneous multislice acquisitions. Magn Reson Med 2014;72:93–102. 7. Barth M, Breuer F, Koopmans PJ, Norris DG, Poser BA. Simultaneous multislice (SMS) imaging techniques. Magn Reson Med 2016;75:63–81. 8. Breuer FA, Blaimer M, Heidemann RM, Mueller MF, Griswold MA, Jakob PM. Controlled aliasing in parallel imaging results in higher acceleration (CAIPIRINHA) for multi-slice imaging. Magn Reson Med 2005;53:684–691. 9. Chollet F et al. Keras. 2015. 10. Wang Z, Bovik AC, Sheikh HR, Member S, Simoncelli EP, Member S. Image Quality Assessment: From Error Visibility to Structural Similarity. 2004;13:600–612.
10. Wang Z, Bovik AC, Sheikh HR, Member S, Simoncelli EP, Member S. Image Quality Assessment: From Error Visibility to Structural Similarity. 2004;13:600–612.

Figures

FIG. 1. Input data proceed from left to right through the different layers. System features similar to coil-sensitivities are derived from the k-space data. These are then merged with the preprocessed image input to unwrap overlapping image content. In the following layers, the channels are combined yielding a single magnitude image per slice, e.g. two unwrapped images for MB=2.

FIG. 2. Comparison of reconstructions for a MB=2 with a CAIPIRIINHA-shift of ¼ FOV. The target data (DLR_trg) represent the ground-truth for the prediction of the DNN (DLR_pred) as well as for standard SSG_stdreconstruction with correct ACS and for reconstructions with incorrect ACS (SSG₀₁, SSG_pha).

FIG. 3. Normalized subtraction maps of all slices are shown. Reconstructions where no correct ACS is available suffer from various artifacts, e.g. inter-slice leakage. DLR (left) without any ACS is compared to SSG with correct ACS, ACS of another head dataset (middle) and ACS of a spherical phantom (right).

FIG. 4. SSIM-maps allow evaluation of errors with perceptual impact. The predicted images of the DNN (left column) show remaining signal of overlapping slices mainly inside the volume while it can be eliminated outside the object. Standard SSG accomplishes a nearly perfect reconstruction in terms of SSIM, while reconstruction deficits appear clearly highlighted for SSG where correct ACS is missing (SSG₀₁, SSG_pha).

TAB. 1. Histograms of the images helped to identify a noise-threshold for masking. Here, a 1% threshold masked was applied to all images to remove contributing noise and allow quantification. NRMSE and MSSIM for the reconstruction of MB=2 datasets are shown in the first and second rows (light gray). The derived metrics for MB=3 with a CAIPIRINHA-shift of 1/3 of the FOV are listed in the bottom rows (darker gray).

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)

2782