2781
Complex-valued residual network learning for parallel MR imaging1Paul C. Lauterbur Research Center for Biomedical Imaging, SIAT, Chinese Academy of Sciences, Shenzhen, China, 2Department of Biomedical Engineering and Department of Electrical Engineering, The State University of New York, Buffalo, NY, United States
Synopsis
Applying deep learning to fast MR imaging has been new and highly evolved. This direction utilizes networks to draw valuable prior information from available big datasets and then assists fast online imaging. Nevertheless, most existing works adopt real-valued network structures while MR images are complex-valued. This paper proposes a complex-valued residual network learning framework for parallel MR imaging. Specifically, complex-valued convolution and initialization strategy are provided. Residual connections are also adopted to learn a more accurate prior. Experimental results show that the proposed method could achieve improved complex-valued image reconstruction with much less time compared to GRAPPA and SPIRiT.
Introduction
Lately, deep learning based fast MR imaging has fascinated many researchers [1-13]. This direction learns and draws prior knowledge from existing high quality big datasets and then assists undersampled MR image reconstruction. As a routinely used fast MR imaging technique, parallel imaging has also been integrated with deep learning [1,2, 12], where multi-coil sensitivity, gradient encoding and valuable prior knowledge have allowed encouraging performances achieved. Nevertheless, most current methods have only exploited real-valued networks while MR images are complex-valued [1-4]. Even when researchers try to keep the complex nature of MR images, the essence of the neural network is still real-valued, which treats real and imaginary parts independently for the convolution [4,5]. Based on our previous framework [1], this paper designs a complex-valued residual network, which allows complex-valued convolutions and provides complex weight initiation strategies. Residual connections are also adopted to avoid the vanishing gradient problems and therefore facilitate to learn a more accurate prior. The learned network then is used to assist online parallel MR imaging.Theory and method
The essence of the proposed approach is complex-valued convolution. To perform the equivalent of a traditional real-valued 2D convolution in the complex domain, we convolve the complex filter matrix$$$W = W_x + iW_y$$$ with an complex image input vector $$$u = u_x + iu_y$$$, where $$$W_x$$$ and $$$W_y$$$ are real matrixes and $$$u_x$$$ and $$$u_y$$$ are real vectors since we are simulating complex arithmetic using real-valued entities. Since convolution operator is distributive, we have $$$W * u = (W_x * u_x - W_y * u_y) + i(W_y * u_x + W_x * u_y)$$$. For neural network learning, proper initialization is critical in reducing the risk of vanishing gradients especially in the case when batch normalization is not adopted. For the initialization of the complex weight $$$W$$$, we adopted Rayleigh distribution for generating the magnitude of $$$W$$$ and used the uniform distribution between $$$-\pi$$$ and $$$\pi$$$ for the phase of $$$W$$$. With the magnitude and phase multiplied, we perform the compete initialization of the complex parameters. Furthermore, residual connections are adopted to provide shortcut paths for easy gradient flow to lower network layers thereby avoiding the vanishing gradient issue of back propagation [14].Experiment
We collected over 3000 fully sampled MR brain slices from a 3T scanner (SIEMENS MAGNETOM Trio) for training. Retrospective undersampled measurements were generated from a 2D poisson distribution by an acceleration factor of 5. The training images were split into 64 by 64 patches and 128 patches were used as a mini-batch for stochastic gradient descent. The network contains three residual blocks and a convolutional layer for reconstruction. Each residual block has two convolutional layers with following configurations (32 feature maps for the 1st layer, 12 for the 2nd layer, both layers with 3×3 kernel size). Training roughly took 14 hours on a machine equipped with 128G memory and a processor of 16 cores (Intel Xeon (R) CPU E5-2680 V3 @2.5GHz). Then we evaluated the trained network on in-vivo transversal brain datasets, which were acquired on a 3T scanner (SIEMENS MAGNETOM Trio) with a 12-channel head coil by T1-weighted turbo spin-echo (TSE) sequence (TE=11.0ms, TR=928ms, FOV=18×18 cm, matrix=256×256, slice thickness=2mm).Results and discussion
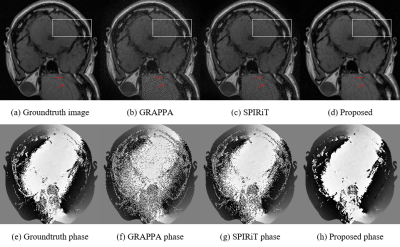
Fig. 2 presents the reconstructions of the GRAPPA (b), SPIRiT (c) and the proposed method (d) with the 2D Poisson undersampling mask at an acceleration factor of 5. For a closer comparison, the white box enclosed areas are also enlarged. It can be observed that the results produced by SPIRiT and GRAPPA still consist of noise, while the proposed method could produce a better image closer to the ground truth. As pointed out by the red arrow, the proposed method can keep some structures that are either lost or blurry in GRAPPA and SPIRiT. Comparing the phase information, our method is also closer to the groundtruth phase image generated from the fully sampled dataset. Furthermore, although the off-line training takes roughly 14 hours, the online test for the proposed method is 7.0 seconds on a workstation on an Ubuntu 14.04 (64-bit) operating system equipped with 128GB RAM and Intel Xeon (R) CPU E5-2680 V3 @2.5GHz in MATLAB 2015b. While GRAPPA and SPIRiT respectively need 439.7 and 14.3 seconds, which consume much more computational time than our method. The quantitative results shown in the table also demonstrate our method produces better results.Conclusion
This work proposes a complex-valued residual network for parallel MR imaging, which allows to keep the complex nature of the MR images. The test results have also shown that the proposed network can reconstruct a more visible-friendly image with better quantitative results in much less time compared to the classical GRAPPA and SPIRiT with the same undersampling mask.Acknowledgements
Grant support: China NSFC 61471350, 61601450, the Natural Science Foundation of Guangdong 2015A020214019, 2015A030310314, the Basic Research Program of Shenzhen JCYJ20140610152828678, and JCYJ20160531183834938, JCYJ20140610151856736 and US NIH R21EB020861 for Ying.References
[1] S. Wang, N. Huang, T. Zhao, Y. Yang, L. Ying, L. Dong, “1D Partial Fourier Parallel MR Imaging with Deep Convolutional Neural Network”, in Proceedings of the International Society of magnetic Resonance in Medicine (ISMRM), 2017, p. 0642
[2] F. Knoll, K. Hammernik, E. Garwood, A. Hirschmann, L. Rybak, M. Bruno, T. Block, J. Babb, T. Pock, D. Sodickson, M. Recht, “Accelerated Knee Imaging Using a Deep Learning Based Reconstruction”, in Proceedings of the International Society of magnetic Resonance in Medicine (ISMRM), 2017, p. 0645
[3] Y.S. Han, D. Lee, J. Yoo, Jong. Y, “Accelerated Projection Reconstruction MR Imaging using Deep Residual Learning”, in Proceedings of the International Society of magnetic Resonance in Medicine (ISMRM), 2017, p. 0690
[4] T. Eo, Y. Jun, T. Kim, J. Jang, D. Hwang, “Cascaded Convolutional Neural Network (CNN) for Reconstruction of Undersampled Magnetic Resonance (MR) Images”, in Proceedings of the International Society of magnetic Resonance in Medicine (ISMRM), 2017, p. 3974
[5] J. Schlemper, J. Caballero, J. Hainal, A. Price, D. Rueckert, “A Deep Cascade of Convolutional Neural Networks for MR Image Reconstruction”, in Proceedings of the International Society of magnetic Resonance in Medicine (ISMRM), 2017, p. 0643
[6] F. Knoll, “Leveraging the Potential of Neural Networks for Image Reconstruction”, in Proceedings of the International Society of magnetic Resonance in Medicine (ISMRM), 2017
[7] B. Zhu, J. Liu, B. Rosen, M. Rosen, “Neural Network MR Image Reconstruction with AUTOMAP: Automated Transform by Manifold Approximation”, in Proceedings of the International Society of magnetic Resonance in Medicine (ISMRM), 2017, p. 0640
[8] S. Wang, T. Zhao, N. Huang, S. Tan, Y. Liu, L. Ying, D. Liang, “Feasibility of Multi-Contrast MR Imaging Via Deep Learning”, in Proceedings of the International Society of magnetic Resonance in Medicine (ISMRM), 2017, p. 3985
[9] S. Wang, T. Xiao, S. Tan, Y. Liu, L. Ying, D. Liang, “Undersampling Trajectory Design for Fast MRI with Super-Resolution Convolutional Neural Network”, in Proceedings of the International Society of magnetic Resonance in Medicine (ISMRM), 2017, p. 3984
[10] K. Hammernik, F. Knoll, D. K. Sodickson, and T. Pock, “Learning a Variational Model for Compressed Sensing MRI Reconstruction”, in Proceedings of the International Society of magnetic Resonance in Medicine (ISMRM), 2016, no. 24, p. 1088
[11] S. Wang, Z. Su, L.Ying, X. Peng, S. Zhu, F. Liang, D. Feng, D. Liang, “Accelerating magnetic resonance imaging via deep learning”, ISBI 514-517 (2016)
[12] K. Kwon, D. Kim, H. Seo, J. Cho, B. Kim, H.W. Park, “Learning-based Reconstruction using Artificial Neural Network for Higher Acceleration”, in Proceedings of the International Society of magnetic Resonance in Medicine (ISMRM), 2016, no. 24, p. 1801
[13] J. Schlemper, J. Caballero, J.V. Hajnal, A. Price, D. Rueckert, “A Deep Cascade of Convolutional Neural Networks for Dynamic MR Image Reconstruction”, IEEE TMI, DOI: 10. 1109/TMI.2017.2760978 (2017)
[14] He, K., Zhang, X., Ren, S., & Sun, J. (2016). Deep residual learning for image recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition (pp. 770-778).
Figures