2776
Simultaneous acquisition of MR angiography and 3D quantitative MR parameter maps1Research & Development Group, Hitachi, Ltd., Tokyo, Japan
Synopsis
We proposed a method to obtain MRA simultaneously with 3D quantitative MR parameter maps. The method calculates MRA by combining images and maps obtained using MR parameter mapping with weights that change in the head-to-neck direction in order to correct for the effect of blood flow. The method was evaluated with five healthy volunteers. It visualized the visibility of blood vessels and correlation of intensity with time-of-flight MRA more effectively than conventional calculation method. This suggests that the proposed method is effective for simultaneously obtaining computational MRA and MR parameter maps.
Introduction
Quantitative MR parameter mapping is expected to enable fast examinations by calculating multiple types of weighted images.1 Previously, we developed a method for simultaneously quantifying multiple MR parameters (proton density, B1, T1, and T2*) by fitting a signal equation to RF-spoiled gradient echo images obtained with various scan parameters.2, 3 Weighted images can be calculated from the MR parameters using a theoretical intensity function. However, theoretical calculation has difficulty computing MR angiography (MRA) because it cannot account for the effect of blood flow. To address this problem, we propose a method for computational MRA, which combines images and maps obtained by quantitative MR parameter mapping with predetermined weights that change in the head-to-neck direction.Method
A 3D RF-spoiled gradient echo sequence was performed on five healthy volunteers using a 3T MRI system (Hitachi, Ltd., Japan) and a 32-channel head coil. Seventeen images were obtained with different scan parameters (flip angle (FA), phase increment of RF (θ), TR, and TE), as shown in Table 1. The other parameters were matrix: 256×256×160, resolution: 0.84×0.84×1.2 mm3, and total acquisition time: 15 min 56 s. Data from the volunteers were obtained according to the standards of the internal review board of the Research & Development Group, Hitachi, Ltd., following receipt of written informed consent.
Maps of proton density, B1, T1, and T2* were obtained from the scanned images using a previously developed method,3 which uses the method of least squares to fit a signal equation based on a Bloch simulation.
A computational MRA of each subject was calculated using the following steps, also shown in Figure 1. In Step 1, the areas of blood vessels and other tissues in four of the five subjects were determined using time-of-flight MRA (TOF-MRA). In Step 2, weights for the linear combination of the intensities of the scanned images and values of the MR parameters were calculated for each axial slice. Fisher’s linear discriminant analysis (LDA)4 was used to determine weights that would make a high-intensity contrast between the blood vessels and the other tissues. In Step 3, the linear combination of the intensities and MR parameters of the one remaining subject were calculated with the predetermined weights. In Step 4, the intensities of the combined image were normalized for each slice so that the mean and the standard deviation become 0 and 1, respectively. These steps were repeated, changing the subject in Step 3 each time, to get the computational MRA of all five subjects. The computation area of the MRA was manually set 114 mm high to include the principal arteries in the brain.
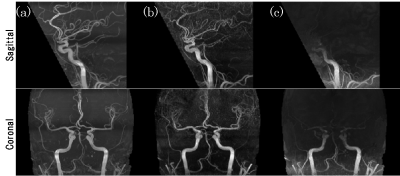
For evaluation, we compared the proposed method with the existing calculation method, which calculates the theoretical intensity of TOF-MRA. The similarities between computational MRA and TOF-MRA were evaluated by analyzing the correlation coefficient of the intensity within 1 voxel of the blood vessels.
Results
The maximum intensity projection of TOF-MRA, computational MRA using the proposed method, and computational MRA using theoretical calculation are shown in Figure 2. Compared to the theoretical calculation, the visibility of blood vessels clearly improved with the proposed method, especially in the upper half of the image. The correlation coefficient with TOF-MRA for the subjects was 0.67±0.07 in the proposed method and 0.50±0.04 in the theoretical calculation (mean ± standard deviation).Discussion
Blood flow changes signal intensity and the calculated MR parameters in the blood vessels in the head-to-neck direction. The proposed method can improve visibility by changing weights to correct for the effect of blood flow. It could enable fast examinations by obtaining MRA in addition to other weighted images calculated from MR parameters. Further study is required to optimize weights for application with many subjects including patients of vascular diseases.Conclusion
We developed a method for computational MRA, which combines images and maps obtained in 3D MR parameter mapping by using predetermined weights that change in the head-to-neck direction. The proposed method visualized blood vessels more effectively than the existing calculation method.Acknowledgements
No acknowledgement found.References
1. Warntjes JBM, Leinhard OD, West J, Lundberg P. Rapid magnetic resonance quantification on the brain: optimization for clinical usage. Magn Reson Med, 2008; 60; 320–329.
2. Taniguchi Y, Yokosawa S, Bito Y. Simultaneous T1, T2, and B1 Mapping Using Partially RF-Spoiled Gradient Echo. Proc. ISMRM, 2011; 4560.
3. Yokosawa S, Taniguchi Y, Amemiya T et al. Fast fitting method for simultaneously quantifying multiple MR parameters using local optimization method with predetermined initial values. Proc. ISMRM, 2017; 1441.
4. Fisher R A, The use of multiple measurements in taxonomic problems. Ann. Hum. Genet. 1936; 7; 179–188