2770

Analytical Characterization of Statistical Bias in Multi-Point Apparent Diffusion Coefficient (ADC) Measurements: Application to Prostate Cancer Imaging

Joshua D. Trzasko¹, Brent A. Warndahl¹, Stephen J. Riederer¹, and Adam T. Froemming¹

¹Mayo Clinic, Rochester, MN, United States

Synopsis

In most diffusion studies, two or more DW images are acquired and an apparent diffusion coefficient (ADC) map is generated, with the goal of providing quantitative diffusion information that is independent of acquisition settings or secondary tissues properties. However, ADC values can vary significantly following protocol changes. In this work, we analytically determine the statistical bias in ADC maps generated from multi-point DWI acquisitions, and show how the derived model rationalizes noise-based error propagation as the source of ADC inconsistencies observed in our own clinical practice.

Purpose

Diffusion-weighted imaging (DWI)¹ is widely used for studying ischemia, and increasingly as a biomarker of elevated tissue cellularity^2,3. For prostate cancer (PCa), DWI-derived information is a primary determinant of lesion scoring under PI-RADSv2⁴. Typically, several differently parameterized DW images are acquired within a series, and a single apparent diffusion coefficient (ADC) map is derived. ADC maps aim to provide quantitative diffusion information that is independent of acquisition settings and/or secondary tissues properties (e.g., T2). However, ADC values can vary significantly following even modest protocol changes^5-8. While it is broadly accepted that such variations are due to noise-based model fitting errors, rigorous mathematical investigation of this phenomenon has been limited – only Saritas et al.⁹ have analytically characterized ADC map noise, for the specific case of monodirectional two b-value acquisitions. Here, we generalize those results for multi-point ($$$\geq2$$$ b-values) acquisitions – commonly used for prostate MRI – and derive a closed-form expression for statistical bias in ADC maps generated using the conventional fitting strategy. Following theory development, we highlight a clinical prostate case where different multi-point DWI acquisitions executed serially yielded different ADC values, and show how the derived model explains these differences.

Theory

For brevity, we herein focus on isotropic diffusion. In a DWI exam that generates $$$T$$$ images, the complex-valued signal at any voxel is modeled as

$$f_{t}=me^{-j\phi_{t}}e^{-TE/T2}e^{-b_{t}ADC}+n_{t}~[EQ1]$$

where $$$m$$$ is background signal, $$$\phi_{t}$$$ is image-dependent phase, $$$b_{t}$$$ is the b-value, and $$$n_{t}$$$ is zero-mean Gaussian noise. As DWI often varies the number of excitations (NEX) with b-value, the per-channel variance of is $$$\sigma_{t}=NEX_{t}\sigma_{0}^{2}$$$. ADC values are typically estimated via linear-least-squares fitting of logarithms of magnitudes of DWIs; specifically,

$$\hat{ADC}=\delta_{2}^{T}\left[ \begin{array}{cc}1&-b_{1}\\\vdots&\vdots\\ 1&-b_{T}\end{array}\right]^{\dagger}\left[\begin{array}{c}\ln|f_{1}|\\\vdots\\\ln|f_{T}|\end{array} \right]~[EQ2]$$

where $$$\delta_{2}^{T}=[0;1]^{T}$$$ and $$$\dagger$$$ denotes the pseudo-inverse. It is readily shown that the bias of this method-of-moments estimator is

$$\mathbb{BIAS}\left[\hat{ADC}\right] =\mathbb{E}\left[\hat{ADC}\right]-ADC=\delta_{2}^{T}\left[ \begin{array}{cc}1&-b_{1}\\\vdots&\vdots\\ 1&-b_{T}\end{array}\right]^{\dagger}\left[\begin{array}{c}\mathbb{E}[\ln|f_{1}|]-\ln|\mathbb{E}[f_{1}]|\\\vdots\\\mathbb{E}[\ln|f_{T}|]-\ln|\mathbb{E}[f_{T}]|\end{array} \right]~[EQ3]$$

Denoting $$$SNR=m/(\sqrt{2}\sigma_{0})$$$, the expected value ($$$\mathbb{E}[\cdot]$$$) of the log-Rician distributed quantity $$$\ln|f_{t}|$$$ is:

$$\mathbb{E}[\ln|f_{t}|]-\ln|\mathbb{E}[f_{t}]|=-\frac{1}{2}Ei\left(-NEX_{t}^{-1}\left(SNR~e^{-TE/T2}e^{-b_{t}ADC}\right)^{2}\right)~[EQ4]$$

where $$$Ei(\cdot)$$$ is the exponential integral^11,9. Using this identity, and after considerable simplification, it follows that:

$$\mathbb{BIAS}\left[\hat{ADC}\right]=\frac{\sum_{t=1}^{T}Ei\left(-NEX_{t}^{-1}\left(SNR~e^{-TE/T2}e^{-b_{t}ADC}\right)^{2}\right)\left(b_{t}{T}-\sum_{s=1}^{T}b_{s}\right)}{2\left(T\left(\sum_{t=1}^{T}b_{t}^{2}\right)-\left(\sum_{t=1}^{T}b_{t}\right)^{2}\right)}~[EQ5]$$

This generalized model enables prediction of shifts in ADC values under multi-point DWI protocol changes, as well as retrospective corroboration that observed ADC shifts are likely due to statistical artifact. The result derived in [REF9] is a special case of our result in EQ5.

Methods

A patient with suspected PCa was sequentially imaged on a GE 3T Discovery 750W using a three-point reduced field-of-view (axial-oblique;22x11cm) DWI sequence (matrix=144x72; ASSET=2; slices=16x4mm; coil=GEM+ERC). For the first protocol (P1), TR/TE=3700/82.8ms, b=[100;1000;1600]s/mm2, and NEX= [5;16;16]; and for the second protocol (P2), TR/TE=4050/69.3ms, b=[100;400;1000]s/mm2, and NEX=[3;5;14]. 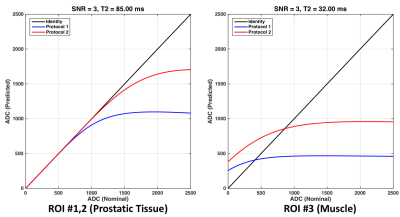All images were reconstructed with complex averaging¹². Region-of-interests (ROIs) were drawn over two suspected restricted diffusion areas within the prostate, and surrounding muscle. T2 values of the prostatic and muscle tissue were presumed to be 85ms and 32ms, respectively^13-14. The (normalized) image SNR was estimated as SNR=3. For each ROI, a plot of the nominal versus predicted ADC values was created over the range [0;2500]mm/s. The generating ADC value was then estimated by minimizing the Euclidean distance between the predicted (i.e., biased estimate) curves and mean ROI values from each ADC image.

Results

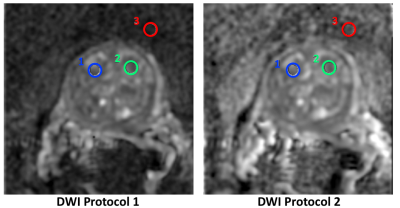
Figure 1 shows cropped enlargements of one slice of the ADC maps generated by the applied protocols, with ROIs demarcated. Figure 2 shows plots of nominal versus predicted (via EQ5) ADC values for each protocol for both prostatic and muscle tissue. Figure 3 includes a table of the mean ADC values measured in each ROI shown in Figure 1. The generating ADC values obtained for the three ROIs via Euclidean projection were: 1198, 1160, and 679mm/s. Using these values, the predicted ADC values for each ROI and protocol are also included in the table in Figure 3. The relative differences between the measured and predicted ADC values are small (<10%), indicating that EQ5 explains the observed shift in ADC values that occurs between the considered protocols.

Discussion

We derived a closed-form mathematical expression for noise-induced bias in ADC maps created from multi-point DWI sequences. This generalized bias model can be used to predict the effects of protocol changes on ADC distributions, and guide the reassignment of diagnostic thresholds. As demonstrated for prostate imaging, this model also enables the feasibility of noise-based error propagation as the source of ADC shift to be interrogated. The bias analysis executed herein readily generalizes from isotropic to anisotropic diffusion, which will be investigated in future work.

Conclusion

Statistical bias in ADC maps generated from multi-point DWI via conventional fitting procedures can be exactly characterized, enabling better understanding of existing DWI protocols and objective assessment of new ones.

Acknowledgements

This work was supported by the Mayo Clinic Discovery Translation Program.

References

[1] Stejskal EO, Tanner JE. Spin diffusion measurements: Spin echoes in the presence of a time-dependent field gradient. J Chem Phys 1965;42:288–92

[2] Zelhof B et al. Correlation of diffusion-weighted magnetic resonance data with cellularity in prostate cancer. BJU Int 2009;103:883–888

[3] Gibbs, P et al. Correlation of ADC and T2 measurements with cell density in prostate cancer at 3.0 Tesla. Inv Radiol 2009;44:572-576

[4] Weinreb JC et al. PI-RADS Prostate Imaging-Reporting and Data System:2015,Version 2. Eur Urol 2016;69:16-40 [5] Jones, DK et al. Optimal strategies for measuring diffusion in anisotropic systems by magnetic resonance imaging. MRM 1999;42:515-525

[6] Alexander DC et al. A general framework for experiment design in diffusion MRI and its application in measuring direct tissue microstructure features. MRM 2008;60:439–448

[7] Sugimura, K. Clinical utility of apparent diffusion coefficient values obtained using high bvalue when diagnosing prostate cancer using 3 Tesla MRI: Comparison between ultra-high bvalue (2000 s/mm2) and standard high b-value (1000 s/mm2). JMRI 2012;36:198–205

[8] Kim CK et al. High-b-Value Diffusion-Weighted Imaging at 3 T to Detect Prostate Cancer: Comparisons Between b Values of 1,000 and 2,000 s/mm2. AJ Roentg 2010;194:W33-W37

[9] Sariitas E et al. SNR dependence of optimal parameters for apparent diffusion coefficient measurements. IEEE TMI 2011;30:424-437

[10] Jones D. Diffusion MRI, Oxford University 2010

[11] Lapidoth A and Moser S. Capacity bounds via duality with applications to multiple-antenna systems on flat-fading channels. IEEE T Info Theory 2003;49: 2426-2467

[12] McKinnon G et al. Phase Corrected Complex Averaging for Diffusion Weighted Spine Imaging. Proc. ISMRM 2000;802.

[13] Yamauichi FL et al. Prostate cancer discrimination in the peripheral zone with a reduced field-of-view T2-mapping MRI sequence, MRI 2015;33:525-30 [

14] Gold GE et al. Musculoskeletal MRI at 3.0 T: relaxation times and image contrast. AJR 2004;183:343-31

Figures

Fig. 1: Cropped ADC maps of a prostate with suspected PCa generated with two different DWI protocols performed sequentially, identically windowed/leveled. Note visually apparent intensity differences in both prostatic (1-2) and muscle (3) tissue.

Fig. 2: Plots depicting nominal versus predicted ADC values under each of the tested DWI protocols, for different tissues types in the defined ROIs. Note that for large ranges of nominal ADC values, the estimated ADC values can significantly differ for the two protocols as well as from the nominal value.

Fig. 3: Table of mean ROI values (in mm/sec x 1e-6) observed in the ADC maps from DWI Protocol 1 (P1) and Protocol 2 (P2), and corresponding values obtained via Euclidean projection of ROI values onto theoretically predicted curves. The small percentage differences between the measured and predicted values strongly suggest that the observed ADC differences are strictly due to noise-based error propagation during model fitting.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)

2770