2767
Joint T1/T2 mapping with frequency-modulated SSFP, radial sampling, and subspace reconstruction1Biomed NMR, Max Planck Institute for Biophysical Chemistry, Goettingen, Germany, 2Institute for Diagnostic and Interventional Radiology, University Medical Center, Goettingen, Germany, 3Partner site Goettingen, German Centre for Cardiovascular Research (DZHK), Goettingen, Germany
Synopsis
In this work, we propose frequency-modulated SSFP imaging with 3D stack-of-stars encoding to perform joint T1/T2 mapping. In contrast to phase-cycled SSFP, inefficient preparation phases are avoided and a subspace-constrained reconstruction allows efficient handling of large data sets. Quantitative mapping is realized by projecting the reconstructed subspace coefficients onto a precomputed piece-wise linear approximation of the Bloch-response manifold. General feasibility is proven by comparison to Gold Standard measurements on a home-brew T1/T2 phantom. The investigated approach is a promising candidate for multi-parametric mapping in vivo.
Introduction
Quantitative imaging has the potential to detect subtle disease effects earlier than conventional imaging. Widespread clinical use of such quantitative methods is mainly hampered by long acquisition times and therefore accelerated quantitative mapping methods are highly desirable1. Recently, balanced SSFP sequences have regained attention due to the intrinsic sensitivity to both, T1 and T2 relaxation times which renders them a suitable candidate for multi-parametric mapping2. In combination with phase-cycling, i.e. the variation of the transmit and receive phase, these steady-state sequences provide a high SNR and become robust to off-resonance effects. However, the acquisition of multiple phase-cycled data sets is time consuming as several independent steady-states have to be prepared via transient phases. An alternative acquisition scheme is frequency-modulated SSFP (fmSSFP)3,4 where the spectral offset frequency is linearly modulated throughout the whole acquisition period such that subsequent readouts correspond to different phase-cycles. Here, we investigate the use of fmSSFP imaging in combination with radial sampling to perform joint T1/T2 mapping.Methods
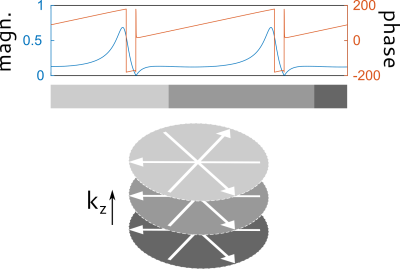
To avoid slice-profile effects a 3D stack-of-stars trajectory is combined with fmSSFP in such a way that one full frequency modulation period is completed within one partition before the next partition is acquired (Fig. 1). When aligning the individual stacks, slice decoding can be performed by inverse Fourier transform along $$$k_z$$$ simplifying the reconstruction from a 3D to a set of 2D problems.
Image reconstruction is formulated as a linear subspace-constrained5 inverse problem of the form
$$$x^{*}=\arg\underset{x}{\min}||y-\mathcal{P}_{\vec{k}}\mathcal{F}_{s}C\mathcal{F}_{t}^{-1}x||_{2}^{2}$$$
where $$$y$$$ denotes the measured raw data, $$$\mathcal{P}_{\vec{k}}$$$ the orthogonal projection onto the sampled trajectory, $$$\mathcal{F}_{s}$$$ the spatial Fourier transform, and $$$C$$$ the (predetermined) coil sensitivity profiles. The low-frequency temporal Fourier basis $$$\mathcal{F}_{t}$$$ spans a subspace in which an arbitrary shift in time domain translates into a linear phase modulation of the subspace coefficients $$$x$$$. Typical fmSSFP time courses are smooth, their corresponding subspace representations exhibit a rapid decay in magnitude toward higher frequencies6 and can be modeled by a small subspace7. The inverse problem is solved within the BART framework8 using a local low-rank regularization on the subspace coefficients. Quantitative maps are generated from the magnitude of the reconstructed subspace coefficients by projecting onto a precomputed piece-wise linear approximation of the Bloch-response manifold generated by numerical simulation of signal responses (not shown).
For validation, we used a home-brew T1/T2 phantom and sequence parameters TR = 5.1 ms, α = 15°, 20 partitions, 16×301 projections per partition, and 1×1×2 mm3 resolution.
Results
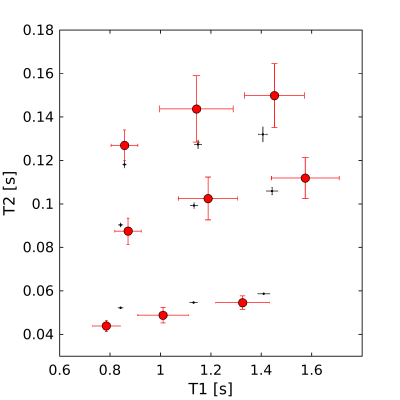
The reconstructed complex subspace coefficients (Fig. 2) decay rapidly in magnitude toward higher frequencies. Off-resonances present in the FOV translate into phase differences, predominantly seen in high frequency coefficients. From this reconstruction, a synthesized image series can be computed that exhibits characteristic moving banding artifacts (Fig. 3). Figure 4 shows the T1, T2 and proton density (PD) map as obtained after projecting the subspace coefficients onto the manifold. All quantitative maps are free of bandings and the designed relaxation time gradients are clearly visible. A quantitative ROI analysis (Fig. 5) reveals a general agreement with Gold Standard measurements (T1: single spin-echo inversion recovery; T2: multi spin-echo). However, systematic deviations from ground truth are visible, particularly for short T2 values.Discussion
A novel fmSSFP-based relaxometry method is proposed for joint T1/T2 mapping which provides an efficient alternative to phase-cycled SSFP imaging. The presented in vitro results demonstrate that fmSSFP sequences can be used to perform joint T1/T2 mapping with minimal preparation phases. The utilized subspace-based reconstruction allows efficient handling of even very large data sets and the subsequent manifold projection allows a fast generation of T1, T2 and spin density maps. However, the source of systematic deviations needs to be understood before optimizing sequence parameters and investigating possible undersampling schemes.Conclusion
The proposed fmSSFP-based relaxometry method minimizes preparation phases and can be combined with efficient 3D encoding. These properties render the investigated approach a promising candidate for multi-parametric mapping in vivo.Acknowledgements
No acknowledgement found.References
[1] Block et al. IEEE Trans Med Imaging 28:1759–1769 (2009)
[2] Shcherbakova et al. Magn Reson Med. 1522–2594, DOI: 10.1002/mrm.26717
[3] Foxall et al. Magn Reson Med. 48:502–508 (2002)
[4] Benkert et al. Magn Reson Med. 73:182–194 (2015)
[5] Petzschner. Magn Reson Med. 66:706–716 (2011)
[6] Nguyen et al. Magn Reson Med. 78:1522–2594 (2017)
[7] Hilbert et al. Magn Reson Med. 1522–2594, DOI: 10.1002/mrm.26836
[8] BART Toolbox for Computational Magnetic Resonance Imaging, DOI: 10.5281/zenodo.592960
Figures